Như vậy, với kích thước khóa là 168 bit, với chiếc máy có thể giải mã 1012 mã trong 1giây (chưa có trong thực tế) thì cũng phải mất tới 5.9 x 1030 năm mới xong.
Vì vậy, nếu sử dụng khóa độ dài 168 ký tự thì có thể coi là an toàn đối với việc phá mã bằng phương pháp vét cạn. Tuy nhiên, với các phương pháp khác thì hệ mã hóa này có thể không an toàn.
Thời gian để dò khóa khi sử dụng phương pháp vét cạn như Bảng
4.1 sau đây.
Bảng 4.1. Thời gian tìm khoá đối với các khoá có kích thước khác nhau
Số lượng khóa | Thời gian cần thiết (1 giải mã/μs) | Thời gian cần thiết (106 giải mã/μs) | |
32 | 232 = 4,3 x 109 | 231 μs = 35,8 phút | 2,15 ms |
56 | 256 = 7,2 x 1016 | 255 μs = 1142 năm | 10,01 giờ |
128 | 2128 = 3,4 x 1038 | 2127 μs = 5,4 x 1024 năm | 5,4 x 1018 năm |
168 | 2168 = 3,7 x 1050 | 2167 μs = 5,9 x 1036 năm | 5,9 x 1030 năm |
26 ký tự | 26! = 4 x 1026 | 2 x 1026 μs = 6,4 x 1012 năm | 6,4 x 106 năm |
(hoán vị) |
Có thể bạn quan tâm!
-
An toàn và bảo mật thông tin: Phần 2 - PGS.TS. Đàm Gia Mạnh, TS. Nguyễn Thị Hội Chủ biên - 1 -
Hệ Mã Hoá Khóa Tự Động (Mã Hóa Cộng Tính Đa Bảng Cải Tiến) -
Ưu Điểm Và Nhược Điểm Của Hệ Mã Hóa Không Đối Xứng -
Một Số Hệ Mã Hóa Không Đối Xứng Khác Khác
Xem toàn bộ 194 trang tài liệu này.
4.1.5.2. Phương pháp thám mã
Dùng để khai thác những nhược điểm của giải thuật mã hóa và dựa trên những đặc trưng chung của nguyên bản hoặc một số cặp nguyên bản
- bản mã mẫu.
Để tiện cho việc nghiên cứu độ an toàn của một giải thuật mã hóa, người ta phân loại ra một số trường hợp để phá mã. Một thuật toán mã hóa nên đảm bảo được độ an toàn trong mọi trường hợp đề ra:
Chỉ có bản mã: Chỉ biết giải thuật mã hóa và bản mã hiện có. Biết nguyên bản: Biết thêm một số cặp nguyên bản - bản mã. Chọn nguyên bản: Chọn 1 nguyên bản, biết bản mã tương ứng.
Chọn bản mã: Chọn 1 bản mã, biết nguyên bản tương ứng. Chọn văn bản: Kết hợp chọn nguyên bản và chọn bản mã.
Trên thực tế có thể gặp tất cả các trường hợp trên. Nhưng khả năng người giải mã chỉ biết giải thuật mã hóa và một số bản mã là lớn nhất và đây cũng là trường hợp khó phá mã nhất.
4.2. HỆ MÃ HÓA ĐỐI XỨNG
4.2.1. Khái niệm về hệ mã hóa đối xứng
Mã hóa khóa đối xứng (hay còn gọi là mã hóa khóa đồng bộ, mã hóa một khóa) là một hệ mã hóa mà trong đó cả hai quá trình mã hóa và giải mã đều dùng chung một khóa mã.
Để đảm bảo tính an toàn, khóa này phải được giữ bí mật. Vì thế các thuật toán mã hóa khóa đối xứng này còn có tên gọi khác là mã hóa với một khóa bí mật (secret key cryptography). Một điều cần lưu ý là khi một người mã hóa một văn bản gốc (plaintext) thành bản mã bằng một khóa K (ciphertext) rồi gửi bản mã cho người nhận thì người nhận sau khi nhận được và muốn giải mã cũng cần phải có khóa K, nghĩa là trước đó hai người gửi và nhận đã phải trao đổi hoặc chia sẻ khóa K cùng nhau.
Có thể hiểu mã hóa đối xứng (mã hoá khoá bí mật) là hệ thống mã hóa mà bên gửi và bên nhận tin cùng sử dụng chung một khóa. Tức là việc mã hóa và giải mã đều dùng một khóa chung. Đây là kỹ thuật mã hóa duy nhất trước những năm 1970 và hiện vẫn được dùng rất phổ biến. Mã hóa đối xứng còn được gọi mà mã hoá khóa riêng hay khóa bí mật để phân biệt với hệ thống mã hóa khóa công khai hay hệ mã hóa hai khóa hiện nay.
Một hệ thống mã hóa đối xứng gồm có 5 thành phần cơ bản gồm:
(1) Nguyên bản: bản thông điệp trước khi được mã hóa hay nguyên
bản.
(2) Giải thuật mã hóa: thuật toán dùng để mã hóa nguyên bản hay
chuyển đổi nguyên bản thành bản mã.
(3) Khóa bí mật: Khóa mã, hay khóa được dùng trong quá trình mã hóa và giải mã.
(4) Bản mã: thông điệp sau khi được mã hóa hay bản mã.
(5) Giải thuật giải mã: thuật toán dùng để giải mã hay chuyển đổi bản mã thành nguyên bản.
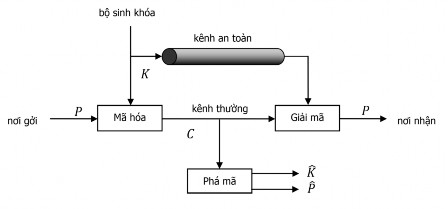
Hình 4.2. Mô hình hệ mã hóa đối xứng
4.2.2. Ưu điểm và nhược điểm của hệ mã hóa đối xứng
Ưu điểm chính của hệ thống mã hóa đối xứng là mô hình khá đơn giản. Mọi người có thể dễ dàng tạo ra được một thuật toán mã hóa đối xứng cho riêng mình.
Chẳng hạn như một thuật toán nhân thông báo với một khóa K nào đó để tạo ra bản mã. Việc giải mã chỉ đơn giản là chia cho K. Với sự đơn giản và rõ ràng của mình, các thuật toán mã hóa đối xứng hiện nay đều dễ cài đặt và hoạt động hiệu quả. So với các thuật toán mã hóa khóa công khai, các thuật toán mã hóa đối xứng hoạt động nhanh và hiệu quả hơn nhiều do tốc độ mã hoá và giải mã cao. Vì vậy, tuy gặp một số nhược điểm nhưng hệ mã hóa đối xứng vẫn được sử dụng trong nhiều ứng dụng hiện nay.
Nhược điểm chính của hệ thống mã hóa đối xứng chính là việc dùng chung khóa của quá trình mã hóa và giải mã. Rõ ràng rằng, khi đã không thể truyền tin trên một kênh truyền tin an toàn thì làm thế nào đảm bảo
được việc truyền khóa bí mật từ người gửi đến người nhận là an toàn. Mâu thuẫn này nảy sinh ra việc muốn có một kênh an toàn để truyền dữ liệu thì trước tiên phải có một kênh an toàn để truyền khoá mã. Trong mô hình mã hóa đối xứng, việc bảo mật và phân phối khóa là công việc khó khăn, phức tạp nhất. Như vậy, tính bảo mật của phương pháp mã hoá này phụ thuộc vào việc giữ bí mật của khóa K, nhưng khóa K thường cũng phải được truyền trên môi trường truyền tin nên rất dễ bị hóa giải (bị “bẻ khóa”).
Mặt khác, không thể gửi thông tin đã mã hóa cho một người nào đó khi không có khả năng gửi khóa cho họ và số lượng khóa sử dụng sẽ rất lớn khi số người tham gia trao đổi thông tin lớn (n(n-1)/2 khóa cho n người).
4.2.3. Các hệ mã hóa đối xứng cổ điển
Các hệ mã hóa đối xứng cổ điển được chia thành hai nhóm: Mã hóa đối xứng cổ điển dựa trên dịch chuyển mã và mã hóa đối xứng cổ điển dựa trên hoán vị.
Các hệ mã hóa đối xứng dựa trên dịch chuyển mã bao gồm: Mã hóa Ceasar (mã hóa cộng); mã hóa nhân, mã hóa Vigenere, mã hóa khóa tự động (mã hóa Vigenere cải tiến),...
Mã hóa đối xứng cổ điển dựa trên hoán vị bao gồm: mã hóa hàng, mã hóa hàng rào, mã hóa khối nhị phân đơn giản và Monophabetic Cipher (mã hóa thay thế),...
4.2.3.1. Hệ mã hóa thay thế Monophabetic Cipher
Hệ mã hóa theo phương pháp này dựa trên phép hoán vị trong một bảng chữ cái nào đó. Chẳng hạn, trên bảng chữ cái tiếng Anh, có thể tiến hành mã hoá như sau:
Bảng 4.2. Ví dụ mã hóa Monophabetic dựa trên bảng chữ cái
a | b | c | d | .......... | x | y | z | |
Ký tự thay thế | F | G | N | T | .......... | K | P | L |
Với thuật toán mã hoá này, ta có: Plaintext: a Bad day
Ciphertext F GFT TFP
Trên đây là một ví dụ mang tính minh họa cho mã hóa thay thế, thực tế, bài toán này có thể sử dụng bất kỳ một hoán vị nào của bảng chữ cái để thực hiện mã hoá, ngoài việc sử dụng bảng chữ cái, có thể sử dụng bất cứ một bảng ký hiệu nào để tiến hành thay thế chuỗi tin cần mã hoá. Xét ví dụ sau:
Bảng 4.3. Mã hóa Monophabetic dựa trên chuỗi nhị phân
000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |
Chuỗi thay thế | 101 | 111 | 000 | 110 | 010 | 100 | 001 | 011 |
Theo bảng này, ta có: Plaintext: 100101111
Ciphertext: 010100011
Với phương pháp mã hoá này, để giải mã chuỗi nhận được, yêu cầu bên nhận tin cũng phải biết khóa được sử dụng để mã hóa, do đó yêu cầu cần có một giao thức để trao đổi khóa giữa người gửi và người nhận tin. Việc trao đổi khóa này là tùy vào người gửi và người nhận, có thể thực hiện đơn giản bằng cách gặp mặt trao đổi trực tiếp, chuyển thông qua mạng Internet, hay nhờ người trung gian,...
4.2.3.2. Hệ mã hóa hàng
Mã hóa hoán vị hàng (Column fence) còn gọi là mã hóa hoán vị đơn bảng với một khóa cho trước, khóa có thể là một hoán vị của k số tự nhiên đầu tiên hoặc là một chuỗi văn bản.
Nguyên tắc của mã hóa hàng là viết các kí tự trong nguyên bản P theo hàng ngang trên k cột, k là số tự nhiên được chọn để lấy hoán vị
hoặc k là số ký tự xuất hiện trong chuỗi ký tự làm khóa. Sau đó, viết lại các kí tự trên từng cột theo thứ tự xuất hiện trong khóa k.
Bảng 4.4. Minh họa mã hóa hàng với K = 4 3 1 2 5 6 7
4 | 3 | 1 | 2 | 5 | 6 | 7 | |
Hàng 1 | A | T | T | A | C | K | P |
Hàng 2 | O | S | T | P | O | N | E |
Hàng 3 | D | U | N | T | I | L | T |
Hàng 4 | W | O | A | M | * | * | * |
Ví dụ: Với nguyên bản: ATTACK POSTPONED UNTIL TWO AM và khóa K là một hoán vị của 7 số tự nhiên đầu tiên. Khóa K=4 3 1 2 5 6 7, khi đó hệ mã hóa được tiến hành theo Bảng 4.4. Khi đó bản mã thu được sẽ là: TTNAAPTMTSUOAODWCOI*KNL*PET*
Ví dụ với nguyên bản: ATTACK POSTPONED UNTIL TWO AM và khóa K = “PRIVATE” là một hoán vị của K như sau K=TEVAPRI, khi đó hệ mã hóa được tiến hành theo bảng sau:
T | E | V | A | P | R | I | |
Hàng 1 | A | T | T | A | C | K | P |
Hàng 2 | O | S | T | P | O | N | E |
Hàng 3 | D | U | N | T | I | L | T |
Hàng 4 | W | O | A | M | * | * | * |
Khi đó bản mã thu được sẽ là: COI*KNL*PET * TTNAAPTMAODWTSUO
Nguyên tắc chung để giải mã hệ mã hóa hàng là chia tổng số ký tự xuất hiện trong bản mã cho tổng số ký tự trong khóa hoặc số tự nhiên K. Sau đó viết lại theo đúng thứ tự của khóa.
Ví dụ với bản mã: TTNAAPTMTSUOAODWCOI*KNL*PET*
Tổng có 28 ký tự, đem chia cho K=7, vậy được các nhóm có 4 ký tự như sau:
TTNA/APTM/TSUO/AODW/COI*/KNL/*PET*
Sau đó viết lại theo khóa K=4 3 1 2 5 6 7 thì ta thu được nguyên bản: ATTACK POSTPONED UNTIL TWO AM ***
4.2.3.3. Hệ mã hóa hàng rào
Hệ mã hóa hoán vị hàng rào (Row fence) cũng là một kiểu hoán vị ký tự dựa trên nguyên tắc xây dựng hàng rào cho các lâu đài từ thời trung cổ, càng nhiều lớp hàng rào thì khả năng bảo vệ càng chắc chắn, các hàng rào được xây dựng xen kẽ nhau nhằm lớp đằng sau hỗ trợ cho lớp đằng trước.
Nguyên tắc chung là dựa trên số lớp hàng rào gọi là khóa K, sau đó viết theo chiều sâu của hàng rào để xây dựng bản mã. Sau đó lấy các ký tự trên từng hàng để làm hoán vị và thu được bản mã.
Ví dụ với nguyên bản: ATTACK AT MIDNIGHT và độ dày của hàng rào là 2 khi đó khóa K=2 và bản mã được xây dựng theo bảng sau:
Bảng 4.5. Minh họa mã hóa hàng rào với K=2
A | T | C | A | M | D | G | T | |
R2 | T | A | K | T | I | N | H |
Khi đó bản mã thu được bằng cách lấy các ký tự trên R1 ghép với các ký tự ở R2 và thu được: ATCAMDIHTAKTINGT
Việc giải mã cũng được thực hiện gần giống như hệ mã hóa hàng, lấy tổng số ký tự chia cho số hàng, sau đó viết lại theo hàng và lấy theo từng cột thì sẽ thu được nguyên bản.
4.2.3.4. Hệ mã hóa Ceasar (Mã hóa cộng tính đơn bảng)
Trong phương pháp này, việc mã hóa được thực hiện bằng cách dịch chuyển chuỗi ký tự trong nguyên bản đi một giá trị cố định nào đó theo trình tự của một bảng chữ cái. Với phương pháp này, khóa mã chính là số được sử dụng để dịch chuyển, phương pháp dịch chuyển lần đầu được Ceasar công bố nên còn được gọi là mã hóa Ceasar. Chẳng hạn, phương pháp mã hóa cộng với khóa K = 3. Khi đó, ta có:
Bảng 4.6. Minh họa mã hóa cộng tính với K=3
a | b | c | d | .......... | x | y | z | |
Ký tự thay thế | D | E | F | G | ......... | A | B | C |
Công thức sử dụng để mã hóa trong phương pháp này là:
Y = X Z,
Trong đó X là chuỗi ký tự cần mã hóa, Z là giá trị của khóa và Y là bản mã thu được, phép tính là phép cộng đồng dư modun 26 (phép chia trung hoa).
Ưu điểm nổi bật của phương pháp này là đơn giản, dễ sử dụng. Tuy nhiên do hạn chế là không gian khóa nhỏ (số lượng khóa có thể sử dụng) nên kẻ tấn công có thể tấn công bằng phương pháp vét cạn và tìm ra khóa khá dễ dàng.
Mã hóa cộng tính với khóa K=3 có thể minh họa trong Hình 5.5.
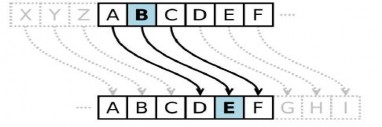
Hình 4.3. Mã hóa cộng tính với bước dịch chuyển bằng 3