Trang chủ / Cơ Sở Dữ Liệu

Các Thông Tin Đầu Vào Của Bài Toán Phân Mảnh Dọc Và Cấp Phát Lớp


định nghĩa bởi các trạng thái và các phương thức của nó. Chúng ta có thể phải thực hiện phân mảnh trạng thái, định nghĩa các phương thức, và cài đặt các phương thức. Hơn nữa, các đối tượng trong một lớp mở rộng có thể được phân mảnh và được đặt ở các vị trí khác nhau, nếu sự phân mảnh được thực hiện chỉ trên trạng thái, các phương thức được nhân bản với mỗi mảnh hay phân mảnh luôn cả các phương thức? Vị trí của các đối tượng tương ứng với định nghĩa lớp của chúng cũng trở thành một vấn đề cần xem xét, kiểu của các thuộc tính cũng thế. Miền của các thuộc tính có thể là các lớp khác. Vì thế, phân mảnh các lớp ứng với một thuộc tính như thế có thể ảnh hưởng tới các lớp khác. Cuối cùng, nếu phân mảnh được thực hiện tương ứng với các phương thức, chúng ta cần phân biệt phương thức đơn giản và phương thức phức. Các phương thức đơn giản là những phương thức không kích hoạt gọi những phương thức khác, còn những phương thức phức có thể kích hoạt phương thức của cùng lớp hoặc các phương thức của các lớp khác.

Tương tự như CSDL quan hệ, chúng ta có hai kiểu phân mảnh cơ bản: phân mảnh dọc, phân mảnh ngang. Ngoài ra, có thể tạo phân mảnh kết hợp từ phân mảnh dọc và phân mảnh ngang.

2.1.2.2. Phân mảnh ngang lớp

Phân mảnh ngang lớp các đối tượng là chia các đối tượng của một lớp thành các phần tách biệt nhau, mỗi phần gồm một số đối tượng. Phân mảnh ngang thực hiện theo các vị từ (predicate) được định nghĩa trên các thuộc tính của lớp. Phân mảnh ngang của một lớp C tạo ra các mảnh f1… fn, mỗi lớp nhận các thể hiện của C thỏa vị từ phân hoạch cụ thể.

Ví dụ 2.1: Xét định nghĩa lớp DongCo

Class DongCo as Object attributes

so_XyLanh: Integer dungTich: Real maLuc: Integer

Trong định nghĩa này, tất cả mọi thuộc tính đều thuộc loại đơn giản. Xét hai vị từ phân hoạch:



p1: maLuc <= 150 p2: maLuc > 150

Trong trường hợp này, DongCo có thể được phân hoạch thành hai mảnh DongCo1 và DongCo2. DongCo được định nghĩa lại thành lớp trừu tượng, hai lớp DongCo1 và DongCo2 kế thừa lại tất cả các tính chất của lớp DongCo. Các đối tượng của lớp DongCo được phân phối cho các lớp DongCo1 và DongCo2 dựa trên giá trị của thuộc tính maLuc của chúng.

Phân mảnh ngang phức tạp hơn khi các vị từ không tách biệt và các thuộc tính cũng như phương thức không phải loại đơn giản. Phức tạp nhất là trường hợp một lớp có các thuộc tính phức và các phương thức phức. Trong trường hợp này, mối liên hệ kiểu con, mối liên hệ hợp phần và mối liên hệ của các kích hoạt phương thức cần được xem xét.

2.1.2.3. Phân mảnh dọc lớp

Phân mảnh dọc phức tạp hơn nhiều so với phân mảnh ngang. Cho trước một lớp C, phân mảnh dọc lớp C thành một số mảnh f1, …, fn, mỗi mảnh chứa một số thuộc tính và một số phương thức. Mỗi mảnh sẽ được định nghĩa ít hơn so với lớp ban đầu. Các vấn đề cần phải giải quyết gồm có mối liên hệ sinh kiểu con giữa các lớp cha, các lớp con của lớp ban đầu và các lớp phân mảnh, mối liên hệ giữa các lớp phân mảnh với nhau, và vị trí các phương thức. Nếu tất cả các phương thức đều là đơn giản thì chúng có thể được phân hoạch dễ dàng. Tuy nhiên, nếu các phương thức là phức tạp thì vị trí của chúng là một vấn đề cần được giải quyết.

2.1.2.4. Các thuật toán phân mảnh lớp

Vấn đề chính của phân mảnh lớp là cải thiện hiệu năng hệ thống bằng cách làm giảm đi các truy xuất dữ liệu không cần thiết. Vì vậy, phân mảnh lớp là một kỹ thuật thiết kế CSDL logic, trong đó, nó cấu trúc lại lược đồ CSDL đối tượng dựa trên ngữ nghĩa ứng dụng. Cần chú ý rằng phân mảnh lớp phức tạp hơn nhiều so với phân mảnh quan hệ, và nó cũng là bài toán NP-đầy đủ. Các thuật toán phân mảnh lớp đặt nền tảng trên cách tiếp cận tương quan và chi phí.

Phương pháp dựa trên tương quan: Tương quan giữa các biến thể hiện và tương quan giữa các phương thức có thể được sử dụng để phân mảnh ngang và


phân mảnh dọc các lớp. Ezeife và Barker đã phát triển các thuật toán phân mảnh ngang [25] và dọc [24] lớp dựa trên việc phân loại thuộc tính và phương thức theo kiểu đơn giản hoặc phức tạp.

Phương pháp dựa trên chi phí: Người ta đã chứng minh rằng các lược đồ phân mảnh dựa trên cách tiếp cận tương quan không phải lúc nào cũng giảm được truy xuất đĩa nhiều nhất khi xử lý một tập các ứng dụng. Vì vậy, Fung và các cộng sự

[26] đã phát triển một mô hình chi phí theo số lượng truy cập đĩa để xử lý các truy vấn và phương thức trên một CSDL HĐT PT.

2.1.3. Cấp phát lớp

Cấp phát lớp là phân bố các lớp vào các trạm khác nhau trong mạng liên kết. Do tính đóng gói của CSDL HĐT, bài toán cấp phát lớp liên quan đến cấp phát phương thức. Việc cấp phát phương thức cần truy xuất đến nhiều lớp tại các vị trí khác nhau là một bài toán cần được nghiên cứu. Bốn lựa chọn được đưa ra [4]:

1. Hành vi cục bộ - đối tượng cục bộ: Đây là trường hợp đơn giản nhất khi mà hành vi và đối tượng áp dụng đều ở cùng một chỗ.

2. Hành vi cục bộ - đối tượng ở xa: Đây là trường hợp mà hành vi và đối tượng áp dụng nằm ở vị trí khác nhau. Có hai cách giải quyết trường hợp này: Một là di chuyển đối tượng ở xa về vị trí chứa hành vi. Hai là di chuyển cài đặt hành vi về vị trí của đối tượng, điều này có thể làm được nếu vị trí nhận có thể cho chương trình chạy được.

3. Hành vi ở xa – đối tượng cục bộ: Ngược lại của trường hợp 2.

4. Hành vi ở xa – đối tượng ở xa: Ngược lại của trường hợp 1.

Chưa có nhiều nghiên cứu đề cập đến vấn đề cấp phát trong CSDL HĐT PT. Trong [13], K. Barker và S. Bhar đã đưa ra các khái niệm cơ bản để thiết lập mô hình cho bài toán cấp phát lớp, trong đó các tác giả cũng đề nghị một hướng tiếp cận đồ thị để giải quyết bài toán cấp phát lớp. Trong [6] và [37] đã đề cập đến thuật toán di truyền để chọn ra phương án cấp phát gần tối ưu. Các thuật toán heuristic cho bài toán cấp phát lớp trong CSDL HĐT PT được đề cập trong [14] và [29]. Trong các thuật toán trên, cấp phát chỉ được thực hiện sau khi giai đoạn phân mảnh đã hoàn thành.


2.2. Các thông tin đầu vào của bài toán phân mảnh dọc và cấp phát lớp

2.2.1. Thông tin về CSDL

Dữ liệu trong CSDL HĐT bao gồm tập các đối tượng được đóng gói, mỗi đối tượng bao gồm các thuộc tính và phương thức. Các đối tượng là các thể hiện từ các lớp, trong phân cấp kế thừa.

Định nghĩa 2.1 [24]: Một lớp thứ i trong CSDL HĐT được biểu diễn bởi Ci

= (Ki, Ai, Mi, Ii) trong đó: Ki là tập các định danh, Ai là tập các thuộc tính, Mi là tập các phương thức và Ii là tập các đối tượng được định nghĩa bởi Ai và Mi.

Thuộc tính của một lớp chia thành hai kiểu đơn giản và phức tạp: Thuộc tính đơn giản là thuộc tính có miền giá trị là các kiểu, lớp nguyên thủy. Thuộc tính phức tạp là thuộc tính có miền giá trị không phải là các lớp nguyên thủy, khi đó giá trị thuộc tính có thể là định danh của các đối tượng khác, được gọi là các thuộc tính tham chiếu.

Phương thức trong một lớp cũng chia thành hai kiểu đơn giản và phức tạp: Phương thức đơn giản là phương thức khi thực hiện không gọi các phương thức khác. Phương thức phức tạp là phương thức khi thực hiện gọi, kích hoạt các phương thức khác trong cùng lớp đó hoặc các phương thức của lớp khác.

Ví dụ 2.2: Giả sử CSDL gồm các lớp: NhanSu (Nhân sự), GiaoVien (Giáo viên), CanBo (Cán bộ), GiaoVienMoi (Giáo viên mời), Khoa (Khoa) và LopHoc (Lớp học). Hai lớp GiaoVien và CanBo kế thừa từ lớp NhanSu, lớp GiaoVienMoi kế thừa từ lớp GiaoVien. Lớp Khoa có chứa các thuộc tính là các đối tượng thuộc lớp GiaoVien, lớp GiaoVien có chứa thuộc tính là đối tượng của lớp LopHoc. Liệt kê các thuộc tính và các phương thức của các lớp như sau:

NhanSu ={{soCMT, ten, ngaySinh, diaChi}, {docSoCMT(), docTen(), docNgaySinh(), docDiaChi()}}

GiaoVien = {{maSoGV, loaiGV, khoa, dsLopDay},{hienThiMaSo_LoaiGV(),docKhoa(), hienThiLopDay(), tinhSoGio()}}

GiaoVienMoi= {{coquan},{docCoquan()}}


CanBo = {{masoCB, phongBan}, {docMaSoCB(), docPhongBan()}}

Khoa = {{tenKhoa, diachi, truongKhoa}, {docTenKhoa(), docDiaChi()}}

LopHoc = {{masoLopHoc, soGio}, {docMaSoLopHoc(), docSoGio()}}

Lớp Khoa là lớp chứa lớp GiaoVien vì thuộc tính truongKhoa là một đối tượng thuộc lớp GiaoVien, tương tự lớp GiaoVien chứa lớp LopHoc. Trong lớp GiaoVien có phương thức tinhSoGio() gọi đến phương thức docSoGio() của lớp LopHoc.

Định nghĩa 2.2: Một phương án phân mảnh dọc của một lớp Ci là một cách chia Ci thành tập các mảnh {𝑓𝑖, 𝑓𝑖,..., 𝑓𝑖}, mỗi mảnh 𝑓𝑖= {Ki, 𝐴𝑖 , 𝑀𝑖, Ii}, (v =

1 2 𝑛 𝑣 𝑣 𝑣

1,..., n), trong đó 𝐴𝑖 là tập con của Ai, 𝑀𝑖 là tập con của Mi.

𝑣 𝑣

Cũng như CSDL quan hệ, phân mảnh dọc phải đảm bảo ba luật phân mảnh, cụ thể trong CSDL HĐT ba luật này thể hiện như sau:

𝑗

- Tính đầy đủ (completeness): Mỗi thuộc tính hoặc phương thức trong lớp Ci phải được tìm thấy trong ít nhất một mảnh 𝑓𝑖.

- Tính tái cấu trúc được (reconstruction): Có khả năng tái cấu trúc lại lớp Ci từ các mảnh tương ứng đã được phân chia.

j

- Tính tách biệt (disjointness): Chỉ định danh và các phương thức truy cập định danh mới được lặp lại trong các mảnh, các thuộc tính và phương thức khác của một lớp Ci chỉ thuộc duy nhất một mảnh 𝑓𝑖. Tính tách biệt có

thể được nới lỏng chỉ áp dụng cho thuộc tính, lúc đó phương thức có thể nhân bản lặp lại trong các mảnh. Hoặc tính tách biệt có thể nới lỏng chỉ áp dụng cho phương thức, lúc đó các thuộc tính có thể nhân bản lặp lại trong các mảnh.

Định nghĩa 2.3: Một phương án cấp phát cho lớp Ci là định vị tập các mảnh

{𝑓𝑖, 𝑓𝑖,..., 𝑓𝑖} của lớp Ci vào một tập các trạm S = {s1, s2, …, sk} trong mạng liên

1 2 𝑛

kết sao cho tổng kích thước các mảnh tại mỗi trạm không vượt quá kích thước của


trạm. Nếu khả năng lưu trữ của các trạm không hạn chế thì có thể bỏ qua tham số kích thước các trạm.

Định nghĩa 2.4: Với mỗi phương thức 𝑚𝑖 và một thuộc tính 𝑎𝑖 của một lớp

𝑗 𝑙

Ci, giá trị MAU(𝑚𝑖, 𝑎𝑖) được định nghĩa như sau:

𝑗 𝑙


𝑖


1 Nếu 𝑚𝑖 sử dụng 𝑎𝑖

𝑀𝐴𝑈(𝑚 , 𝑎𝑖) = { 𝑗 𝑙

𝑗 𝑙

0 Ngược lại

MAU với dụng ý viết tắt của Method Attribute Usage mang ý nghĩa sự sử dụng thuộc tính của phương thức. Thiết lập tất cả các giá trị MAU(𝑚𝑖, 𝑎𝑖) cho tất

𝑗 𝑙

cả các phương thức và thuộc tính của lớp Ci nhận được ma trận phương thức sử dụng thuộc tính MAUi.

Ví dụ về ma trận MAU của lớp GiaoVien như Bảng 2.1.


a1 (maSoGV)

a2

( loaiGV)

a3 (khoa)

a4 (dsLopDay)

m1(hienThiMaSo_LoaiGV())

1

1

0

0

m2(docKhoa())

0

0

1

0

m3 (hienThiLopDay())

0

0

0

1

m4(tinhSoGio())

0

0

0

1

Có thể bạn quan tâm!

Xem toàn bộ 136 trang tài liệu này.

Xử lý và tối ưu hóa truy vấn trong cơ sở dữ liệu hướng đối tượng phân tán - 7

Bảng 2.1: Ma trận MAU của lớp GiaoViên


𝑗

Định nghĩa 2.5: Với mỗi phương thức 𝑚𝑖 của của một lớp Ci và một phương thức 𝑚ℎ của một lớp Ch, giá trị MMU(𝑚𝑖, 𝑚ℎ ) được định nghĩa như sau:

𝑙 𝑗 𝑙

𝑖 1 Nếu 𝑚𝑖 sử dụng 𝑚ℎ

𝑀𝑀𝑈(𝑚 , 𝑚ℎ ) = { 𝑗 𝑙

𝑗 𝑙

0 Ngược lại

MMU với dụng ý viết tắt của Method Method Usage mang ý nghĩa sự sử dụng phương thức của phương thức.


2.2.2. Thông tin về ứng dụng

Với tính đóng gói của các đối tượng, các truy vấn ứng dụng thường truy cập các đối tượng thông qua các phương thức.

𝑗

Định nghĩa 2.6: Với mỗi truy vấn 𝑞𝑖 truy cập vào lớp Ci và một phương thức

𝑚𝑖 của lớp Ci, giá trị 𝑄𝑀𝑈(𝑞𝑖 , 𝑚𝑖 ) được định nghĩa như sau:

𝑙 𝑗 𝑙


𝑖


1 Nếu 𝑞𝑖 sử dụng 𝑚𝑖

𝑙

𝑄𝑀𝑈(𝑞𝑗

, 𝑚𝑖 ) = {

𝑗 𝑙

0 Ngược lại

QMU với dụng ý viết tắt của Query Method Usage mang ý nghĩa sự sử dụng phương thức của truy vấn ứng dụng. Thiết lập tất cả các giá trị 𝑄𝑀𝑈(𝑞𝑖 , 𝑚𝑖 ) cho

𝑗 𝑙

tất cả các truy vấn vào lớp Ci với các phương thức của lớp Ci nhận được ma trận truy vấn sử dụng phương thức QMUi.

Ví dụ 2.3: Giả sử có 3 truy vấn q1, q2, và q3 tới lớp GiaoVien.

q1: Tìm số chứng minh thư và hiển thị lớp dạy của một giáo viên có mã số nào đó.

q2: Tìm mã giáo viên và loại giáo viên của tất cả các giáo viên của một khoa nào đó.

q3: Liệt kê khoa của những giáo viên có số giờ dạy nhỏ hơn 50.

Ma trận QMU của lớp GiaoVien là Bảng 2.2, chú ý bốn phương thức m1, m2, m3, m4 là bốn phương thức nguyên thủy của lớp Giaoviên, phương thức m5 là phương thức docSoCMT() của lớp NhanSu và m6 là phương thức docSoGio() của lớp LopHoc.

Bảng 2.2: Matrận QMU của lớp Giáo viên




m1


m2


m3


m4

m5 (NhanSu.docSoCMT())

m6 (LopHoc.docSoGio())

q1

1

0

1

0

1

0

q2

1

1

0

0

0

0

q3

0

0

0

1

0

1


𝑗

𝑗

Định nghĩa 2.7: Với mỗi truy vấn 𝑞𝑖 truy cập vào lớp Ci và một trạm sk trong mạng kết nối, giá trị tần suất truy cập của truy vấn vào các trạm 𝑄𝑆𝐹(𝑞𝑖 , 𝑠𝑘) là số

𝑗

lần truy cập của truy vấn 𝑞𝑖 vào trạm sk.

𝑗

QSF với dụng ý viết tắt của Query Site Frequency mang ý nghĩa tần suất truy cập vào trạm của truy vấn ứng dụng. Thiết lập tất cả các giá trị 𝑄𝑆𝐹(𝑞𝑖 , 𝑠𝑘) cho tất cả các truy vấn vào lớp Ci với tất cả các trạm sk nhận được ma trận tần suất truy cập các truy vấn vào các trạm QSFi. Ví dụ về ma trận tần suất truy cập trạm được chỉ ra trong Bảng 2.3.

Bảng 2.3: Ma trận QSF của lớp Giáo viên



s1

s2

s3

q1

10

5

10

q2

5

40

0

q3

25

15

5


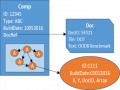
Ma trận QMU và QSF của các ứng dụng truy cập vào các lớp trong CSDL tại các trạm như Hình 2.1.

Chú ý rằng các truy vấn vào 2 lớp GiaoVien và CanBo sẽ sử dụng một số phương thức từ lớp cha NhanSu, vì vậy ma trân QMU của lớp GiáoVien và CanBo sẽ phải bổ sung thêm các phương thức này. Ma trận QMU của lớp GiaoVien có sáu cột, bốn cột đầu biểu diễn sự truy cập các phương thức m1, m2, m3, m4 của chính lớp GiaoVien, cột thứ năm biểu diễn sự truy cập tới phương thức m5 của lớp NhanSu, cột cuối cùng chỉ ra sự truy cập tới phương thức m6 của lớp LopHoc. Ở đây giả sử lớp CanBo không có truy vấn nào nên bỏ qua ma trận QMU và QSF.

Trong Hình 2.1, những phương thức không phải là phương thức nguyên thủy của lớp được phân biệt bằng cách in nghiêng. Lưu ý chỉ số của các phương thức và truy vấn được phân biệt giữa các lớp, ví dụ mi của lớp NhanSu khác mi của lớp GiaoVien, qi của lớp NhanSu khác qi của lớp GiaoVien.

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Ngày đăng: 10/06/2022