Một Số Kiến Trúc Convolutional Neural Network Thông Dụng

(bias), tổng số 23,550 tham số (parameter). Nói cách khác, lớp kết nối đầy đủ (fully

– connected layer) sẽ cần số lượng tham số nhiều gấp 40 lần so với lớp tích chập (convolutional layer).

Tất nhiên, không thể thực sự làm một so sánh trực tiếp giữa số lượng các tham số, bởi vì hai mô hình này khác nhau. Nhưng về trực giác dường như việc sử dụng bất biến dịch của các lớp tích chập sẽ giảm số lượng các tham số cần thiết mà vẫn đạt được hiệu quả giống như các mô hình kết nối đầy đủ. Mô hình mạng tích chập sẽ cho kết quả huấn luyện nhanh hơn giúp xây dựng mạng sâu hơn sử dụng các lớp tích chập. Cái tên “convolutional” xuất phát là các hoạt động trong phương trình đôi khi được biết đến như convolution. Chính xác hơn một chút, đôi khi viết phương trình như: a1 = σ (b + w * a0), trong đó a1 là tập kích hoạt đầu ra từ một bản đồ đặc trưng, a0 là tập hợp các kích hoạt đầu vào, và * được gọi là phép toán chập.

Lớp chứa hay lớp tổng hợp (Pooling layer): Ngoài các lớp tích chập vừa mô tả, mạng neuron tích chập cũng chứa các lớp pooling. Lớp pooling thường được sử dụng ngay sau lớp tích chập. Những gì các lớp pooling làm là đơn giản hóa các thông tin ở đầu ra từ các lớp tích chập.

Ví dụ, mỗi đơn vị trong lớp pooling có thể thu gọn một vùng 2 × 2 neuron trong lớp trước. Một thủ tục pooling phổ biến là max-pooling. Trong max- pooling, một đơn vị pooling chỉ đơn giản là kết quả đầu ra kích hoạt giá trị lớn nhất trong vùng đầu vào 2

× 2, như minh họa trong sơ đồ sau:

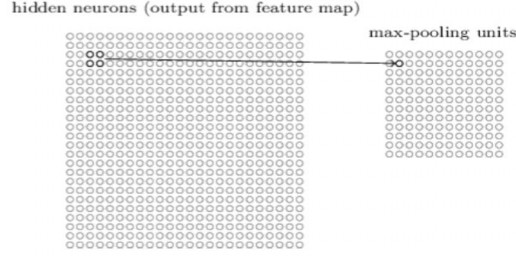
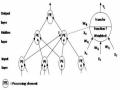
Hình 2.14 Sơ đồ phân lớp

Bởi vì có 24 × 24 neuron đầu ra từ các lớp tích chập, sau khi pooling có 12 × 12 neuron. Như đã đề cập ở trên, lớp tích chập thường có nhiều hơn một bản đồ đặc trưng, áp dụng max-pooling cho mỗi bản đồ đặc trưng riêng biệt. Vì vậy, nếu có ba bản đồ đặc trưng, các lớp tích chập và max-pooling sẽ kết hợp như sau:

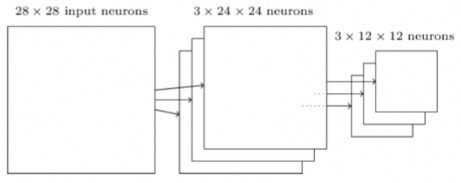
Hình 2.15 Sơ đồ phân lớp

có thể hiểu max-pooling như là một cách cho mạng để hỏi xem một đặc trưng nhất được tìm thấy ở bất cứ đâu trong một khu vực của ảnh. Sau đó nó bỏ đi những thông tin định vị chính xác. Trực giác là một khi một đặc trưng đã được tìm thấy, vị trí chính xác của nó là không quan trọng như vị trí thô của nó so với các đặc trưng khác. Một

lợi ích lớn là có rất nhiều tính năng gộp ít hơn (fewer pooled features), điều này sẽ giúp giảm số lượng các tham số cần thiết trong các lớp sau.

Max-pooling không phải là kỹ thuật duy nhất được sử dụng để pooling. Một phương pháp phổ biến khác được gọi là L2 pooling. Ở đây, thay vì lấy giá trị kích hoạt tối đa (maximum activation) của một vùng 2 × 2 neuron, chúng ta lấy căn bậc hai của tổng các bình phương của kích hoạt trong vùng 2 × 2. Trong khi các chi tiết thì khác nhau, nhưng về một khía cạnh khác thì tương tự như max-pooling: L2 pooling là một cách để cô đọng thông tin từ các lớp tích chập. Trong thực tế, cả hai kỹ thuật đã được sử dụng rộng rãi, đôi khi người ta sử dụng các loại pooling khác.

Đặt tất cả chúng lại với nhau (Putting it all together): Bây giờ có thể đặt tất cả những ý tưởng lại với nhau để tạo thành một mạng tích chập hoàn chỉnh. Nó tương tự như kiến trúc nhìn vào, nhưng có thêm một lớp 10 neuron đầu ra, tương ứng với 10 giá trị có thể cho các số MNIST ( '0', '1', '2', v.v...):

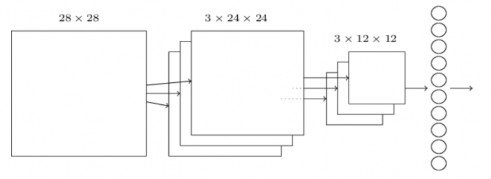
Hình 2.16 Sơ đồ phân lớp

Mạng bắt đầu với 28 × 28 neuron đầu vào, được sử dụng để mã hóa các cường độ điểm ảnh cho ảnh MNIST. Sau đó là một lớp tích chập sử dụng 5 × 5 trường tiếp nhận cục bộ và 3 bản đồ đặc trưng. Kết quả là một lớp 3 × 24 × 24 neuron lớp ẩn.

Bước tiếp theo là một lớp max-pooling, áp dụng cho 2 × 2 vùng qua 3 bản đồ đặc trưng (feauture maps). Kết quả là một lớp 3 × 12 × 12 neuron đặc trưng ở tầng ẩn.

Lớp cuối cùng của các kết nối trong mạng là một lớp đầy đủ kết nối. Đó là, lớp này nối mọi neuron từ lớp max-pooled tới mọi neuron của tầng ra. Kiến trúc kết nối đầy đủ này cũng giống như mô hình sử dụng trong các chương trước.

Kiến trúc tích chập này hoàn toàn khác với các kiến trúc được sử dụng trong các chương trước. Nhưng về tổng thể thì tương tự: mạng cấu tạo từ nhiều đơn vị đơn giản, hành vi của nó được xác định bởi trọng số và độ lệch. Và mục tiêu tổng thể là vẫn như nhau: sử dụng dữ liệu huấn luyện để huấn luyện trọng số và độ lệch của mạng vì vậy mạng hiện tốt việc phân loại các chữ số đầu vào.

Đặc biệt, như phần đầu đã trình bày, sẽ huấn luyện mạng sử dụng gradient descent ngẫu nhiên và lan truyền ngược. Tuy nhiên, cần thay đổi thủ tục lan truyền ngược (backpropagation). Lý do là công thức của lan truyền ngược là cho các mạng với các tầng kết nối đầy đủ, nó đơn giản để thay đổi công thức lan truyền ngược cho các lớp tích chập và các lớp max- pooling

2.5 Một số kiến trúc convolutional neural network thông dụng

2.5.1 Kiến trúc AlexNet [17]

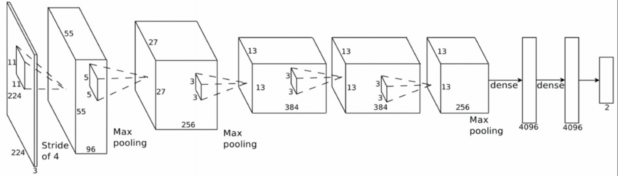
Hình 2.17 Kiến trúc AlexNet

https://www.researchgate.net/figure/AlexNet-CNN-architecture-layers_fig1_318168077

Kiến trúc AlexNet do Alex Krizhevsky phát triển vào năm 2012 để khi tham gia cuộc thi ImageNet. Mô hình này đã đạt giải nhất trong cuộc thi 2012 ImageNet. Mô hình gồm 5 tầng convolitional và 3 tầng fully connected với các tham số như trong hình vẽ trên.

Số lượng tham số: 60 triệu tham số

2.5.2 Kiến trúc VGG 16 [17]

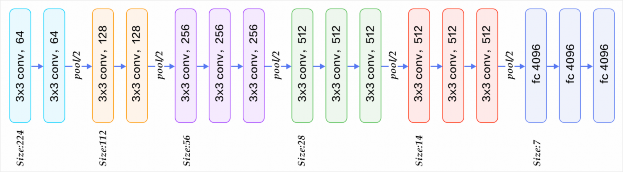
Hình 2.18 Kiến trúc VGG 16

https://www.quora.com/What-is-the-VGG-neural-network

Kiến trúc VGG 16 do Simonyan và Zissermanphát triển vào năm 2014 để khi tham gia cuộc thi ILSVRC 2014. Mô hình này đã đạt giải nhì trong cuộc thi ILSVRC 2014.

Mô hình gồm tổng cộng 16 tầng, trong đó có 13 tầng convolitional và 3 tầng fully connected với các tham số như trong hình vẽ trên.

Số lượng tham số: 138 triệu tham số

2.5.3 Kiến trúc Inception/GoogleNet [18]

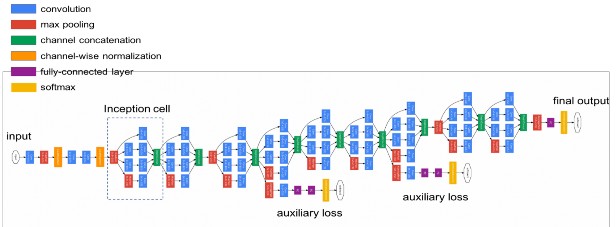
Hình 2.19 Kiến trúc Inception

https://medium.com/coinmonks/paper-review-of-googlenet-inception-v1-winner-of-ilsvlc- 2014-image-classification-c2b3565a64e7

Kiến trúc Inception do Google phát triển và đã chiến thắng trong cuộc thi ILSVRC 2014.

Mô hình gồm 22 tầng convolitional và không có tầng fully connected. Trong mô hình Inception, các tác giả đã đưa ra module đặt tên là Inception. Inception gồm các phép toan filter được thực hiện song song trên input của tầng trước đó. Mỗi inception gồm có 3 convolutional có kích thước (1x1, 3x3, 5x5) và 1 tầng max pooling kích thước 3x3.

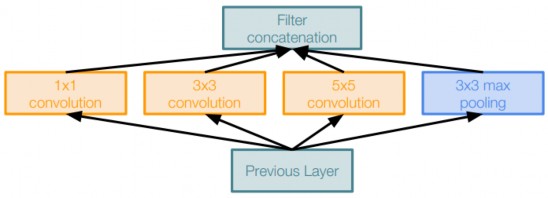
Hình 2.20 Inception

https://medium.com/coinmonks/paper-review-of-googlenet-inception-v1-winner-of-ilsvlc- 2014-image-classification-c2b3565a64e7

Số lượng tham số: 5 triệu tham số

CHƯƠNG 3. PHÂN LOẠI ẢNH TRÁI CÂY

3.1 Phát biểu bài toán

Phân lớp các đối tượng trong ảnh là bài toán quan trọng trong thị giác máy tính, đây là giai đoạn quan trọng trong việc hiểu các đối tượng trong ảnh. Tuy nhiên, cho tới thời điểm này, mặc dù đã có nhiều giải pháp hiệu quả giải quyết bài toán phân lớp trên từng loại cơ sở dữ liệu ảnh cụ thể, bài toán phân lớp ảnh nói chung vẫn còn là bài toán thách thức.

Trong luận văn này sẽ tìm hiểu bài toán phân lớp ảnh trái cây màu. Đầu vào của bài toán là ảnh màu của trái cây có kích thước 100 × 100. Đầu ra của bài toán là mã số màu của ảnh trái cây. Có tất cả 60 loại trái cây.

Ví dụ 1: Một số ảnh quả táo cần nhận dạng

Hình 3.1 Hình dạng khác nhau của cùng một loại táo

Ví dụ 2: Một số ảnh quả Nho cần nhận dạng

Tên trái cây
0	Apple Braeburn
1	Apple Golden 1
2	Apple Golden 2
3	Apple Golden 3
4	Apple Granny Smith
5	Apple Red 1
6	Apple Red 2
7	Apple Red 3

Apple Red Delicious
9	Apple Red Yellow
10	Apricot
11	Avocado
12	Avocado ripe
13	Banana
14	Banana Red
15	Cactus fruit
16	Carambula
17	Cherry
18	Clementine
19	Cocos
20	Dates
21	Granadilla
22	Grape Pink
23	Grape White
24	Grape White 2
25	Grapefruit Pink
26	Grapefruit White
27	Guava
28	Huckleberry
29	Kaki
30	Kiwi
31	Kumquats
32	Lemon
33	Lemon Meyer