Đồ Thị Minh Họa Tổng Chi Phí Và Thời Gian Trả Lời

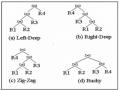
cắt bỏ. Có hai cách: Theo chiều rộng - xây dựng tất cả các kế hoạch có thể trước khi chọn kế hoạch tốt nhất (Quy hoạch động (Dynamic Programming)), theo chiều sâu – chỉ xây dựng một kế hoạch (Greedy).

- Chiến lược ngẫu nhiên (Randomized Strategy): Tiến hành tìm kiếm giải pháp tối ưu xung quanh một số điểm cụ thể. Chiến lược này không đảm bảo kế hoạch tối ưu nhưng tránh chi phí cao trong tối ưu hóa về bộ nhớ và thời gian thực hiện. Chiến lược này áp dụng tốt hơn với câu truy vấn có 5 - 6 quan hệ trở lên. Hai kỹ thuật tiêu biểu là Interative Improvement và Simulated Annealing [4].

2.2.3.2. Mô hình chi phí

Mô hình chi phí của bộ tối ưu hóa gồm có các hàm chi phí để dự đoán chi phí của các toán tử, số liệu thống kê, dữ liệu cơ sở và các công thức để ước lượng kích thước các kết quả trung gian.

Hàm chi phí

Chi phí của một chiến lược thực hiện phân tán có thể được biểu diễn hoặc theo tổng thời gian (total time) hoặc theo thời gian trả lời (response time). Tổng thời gian là tổng của tất cả các thành phần thời gian, còn thời gian trả lời tính từ lúc bắt đầu đến lúc kết thúc câu truy vấn. Công thức chung để tính tổng thời gian như sau:

Total_time = TCPU* #insts + TI/O* #I/Os + TMSG * #msgs + TTR* #bytes Trong đó:

Total_cost: Tổng thời gian;

TCPU: Thời gian của một lệnh CPU;

TI/O: Thời gian cho một thao tác truy xuất/nhập đĩa;

Có thể bạn quan tâm!

Xem toàn bộ 103 trang tài liệu này.

TMSG: Thời gian cố định của việc khởi hoạt và nhận một thông báo;

TTR: Thời gian cần để truyền một đơn vị dữ liệu từ trạm này tới trạm khác, ta xem CTR là hằng số;

#insts, #I/Os, #msgsm, #byte: Tương ứng là tổng trên các trạm của tất cả các số lệnh CPU, số lần truy xuất/ nhập đĩa, số thông báo, kích thước của tất cả các

thông báo.

Trong công thức trên, hai thành phần đầu là thời gian xử lý cục bộ, hai thành phần sau là thời gian truyền. Thời gian truyền #bytes dữ liệu từ trạm này đến trạm khác được giả thiết là một hàm tuyến tính của #bytes.

CT(#bytes) = TMSG + TTR* #bytes

Khi thời gian trả lời của câu truy vấn là hàm mục tiêu của bộ tối ưu thì các xử lý địa phương song song và truyền thông song song phải được xét. Công thức tổng quát tính thời gian trả lời (response time) là:

Response_time = TCPU * seq_#insts + TI/O * seq_#I/Os

+ TMSG * seq_#msgs + TTR * seq_#bytes

Trong đó: seq_#x (x có thể là các lệnh CPU, I/O, các thông báo, các byte) là số lớn nhất của x phải được thực hiện tuần tự đối với sự thực thi của câu truy vấn. Như vậy có thể bỏ qua bất kỳ xử lý và truyền thông được thực hiện song song.

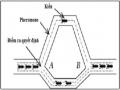
Ví dụ 2.15: Hình 2.17 minh hoạ sự khác nhau giữa tổng thời gian và thời gian trả lời, trong đó máy tính trả lời câu truy vấn tại trạm 3 với dữ liệu từ trạm 1 và trạm 2, ở đây chi phí truyền thông được xét.

Hình 2.17: Đồ thị minh họa tổng chi phí và thời gian trả lời

Giả sử, TMSG và TTR được biểu thị theo đơn vị thời gian. Tổng thời gian truyền x đơn vị dữ liệu từ trạm 1 đến 3 và y đơn vị dữ liệu từ trạm 2 đến trạm 3 là:

Total_time = 2TMSG + TTR*(x+y)

Vì việc truyền dữ liệu có thể thực hiện song song nên thời gian trả lời câu truy vấn là: Response_time = max{TMSG + TTR*x, TMSG + TTR*y}

Thời gian trả lời tối thiểu đạt được bằng cách tăng mức độ xử lý song song,

tuy nhiên không có nghĩa tổng chi phí là tối thiểu. Ngược lại, tổng chi phí có thể tăng khi có nhiều xử lý địa phương và truyền song song hơn.

Số liệu thống kê CSDL

Tác nhân chính ảnh hưởng đến hiệu quả hoạt động của một chiến lược thực thi là kích thước các quan hệ trung gian đã được tạo ra. Khi một phép toán tiếp theo nằm tại một vị trí khác, quan hệ trung gian phải được di chuyển đến đó. Đó chính là điều khiến chúng ta phải ước lượng kích thước của các kết quả trung gian của các phép toán đại số quan hệ nhằm giảm thiểu lượng dữ liệu phải truyền. Việc ước lượng này dựa trên các thông tin thống kê về các quan hệ cơ sở và các công thức để dự đoán lực lượng của các kết quả. Có những được mất giữa tính chính xác của các số liệu thống kê và chi phí quản lý chúng: Số liệu càng chính xác, chi phí càng cao. Đối với một quan hệ R được định nghĩa trên tập thuộc tính A = {A1, A2, ……., An} và được phân mảnh là R1, R2, ……., Rn dữ liệu thống kê điển hình như sau:

- Đối với mỗi thuộc tính Ai chiều dài (theo số byte) được ký hiệu là length (Ai), và đối với mỗi thuộc tính Ai của mỗi mảnh Rj, số lượng phân biệt các giá trị của Ai, là lực lượng khi chiếu mảnh Rj trên Ai , được ký hiệu là card (π Ai (Rj)).

- Ứng với miền của mỗi thuộc tính Ai trên một tập giá trị sắp thứ tự được (ví dụ số nguyên hoặc số thực), giá trị lớn nhất và nhỏ nhất được ký hiệu là max(Ai) và min(Ai).

- Ứng với miền của mỗi thuộc tính Ai lực lượng của miền được ký hiệu là card(dom[Ai]). Giá trị này cho biết số lượng các giá trị duy nhất trong dom[Ai].

- Số lượng các bộ trong mỗi mảnh Rj được ký hiệu là card(Rj)

Đôi khi dữ liệu thống kê cũng bao gồm hệ số chọn nối (join selectivity factor) đối với một số cặp quan hệ, nghĩa là tỷ lệ các bộ có tham gia vào nối. Hệ số chọn

nối được ký hiệu là SFj của quan hệ R và S là một giá trị thực giữa 0 và 1:

( ⋈ )

( ) ( )

Chẳng hạn hệ số chọn nối 0.5 tương ứng với một quan hệ nối cực lớn, trong khi đó hệ số 0.001 tương ứng với một quan hệ khá nhỏ. Chúng ta nói rằng nối có độ chọn kém trong trường hợp đầu và độ chọn tốt trong trường hợp sau.

Dữ liệu thống kê này rất có ích cho việc dự đoán kích thước quan hệ trung

gian.

Size (R) = card (R) * length (R)

Trong đó length (R) là chiều dài (theo byte) của một bộ của R, được tính từ

các chiều dài của các thuộc tính của R. Việc ước lượng card (R), số lượng các bộ trong R, đòi hỏi phải sử dụng các công thức được cho trong phần tiếp theo.

Lực lượng của các kết quả trung gian

Dữ liệu thống kê rất có ích khi đánh giá lực lượng của các kết quả trung gian. Hai giả thiết đơn giản thường được đưa ra về CSDL. Phân phối của các giá trị thuộc tính trong một quan hệ được giả định là thống nhất và tất cả mọi thuộc tính đều được độc lập, theo nghĩa là giá trị của một thuộc tính không ảnh hưởng đến giá trị của các thuộc tính khác. Hai giả thiết này thường không đúng trong thực tế, tuy nhiên chúng làm cho bài toán dễ giải quyết hơn. Dưới đây sẽ trình bày các công thức ước lượng, lực lượng các kết quả của các phép toán đại số cơ bản (phép chọn, phép chiểu, tích Descartes, nối, nối nửa, hợp, và hiệu). Quan hệ toán hạng được ký hiệu là R và S. Hệ số chọn của một phép toán đó được biểu thị là SFOP, với OP biểu thị cho phép toán.

Phép chọn. Lực lượng của phép chọn là: Card(σF(R)) = SFS(F) * card(R)

Trong đó SFS(F) phụ thuộc vào công thức chọn và có thể được tính như sau,

với p(Ai) và p(Aj) biểu thị cho vị trí từ thuộc tính Ai và Aj.

( )

(( ))

( )()

( ) ( )

( )()

( ) ( )

SFS (p(Ai) ٨ p(Aj)) = SFS (p(Ai) * SFS (p(Aj))

SFS (p(Ai) ۷ p(Aj)) = SFS (p(Ai) * SFS (p(Aj)) – (SFS (p(Ai)) * SFS (p(Aj)))

SFS (Ai  {value}) = SFS (A = value) * card({values})

Phép chiếu. Chiếu có thể loại bỏ hoặc không loại bỏ các bộ giống nhau. Ở đây chúng ta xem như chiếu có kèm theo cả việc loại bỏ này. Một phép chiếu bất kỳ rất khó ước lượng chính xác bởi vì mối tương quan giữa các thuộc tính được chiếu thường không được biết. Tuy nhiên, có hai trường hợp đặc biệt có ích nhưng việc ước lượng hoàn toàn tầm thường. Nếu chiếu của quan hệ R dựa trên thuộc tính A duy nhất, lực lượng chỉ là số bộ thu được khi thực hiện phép chiếu. Nếu một trong các thuộc tính chiếu là khóa của R thì card (πA(R)) = card(R)

Tích Descartes. Lực lượng của tích Descartes của quan hệ R và S là

card (R x S) = card(R)* card(S)

Phép nối. Không có một phương pháp tổng quát nào để tính lực lượng của phép nối mà không cần thêm thông tin bổ sung. Cận trên của lực lượng cho phép nối là lực lượng của tích Đề các. Một số hệ thống, chẳng hạn như hệ INGRES phân tán sử dụng cận trên này. R* sử dụng thương số của cận trên này với một hằng số, phản ánh sự kiện là kết quả nối luôn nhỏ hơn tích Đề các. Tuy nhiên, có một trường hợp xảy ra khá thường xuyên nhưng việc ước lượng lại khá đơn giản. Nếu R được thực hiện phép nối bằng với S trên thuộc tính A của R và thuộc tính B của

S, trong đó A là khóa của quan hệ R và B là khóa ngoại của quan hệ S thì lực lượng của kết quả đó có thể tính xấp xỉ là: Card (R A=B S) = card(S)

Bởi vì mỗi bộ của S khớp với tối đa một bộ của R. Điều này cũng đúng nếu B

là khóa của S và A là khóa ngoại của R. Tuy nhiên, ước lượng này là cận trên bởi vì nó giả sử rằng mỗi bộ của S đều tham gia vào trong nối. Đối với những nối quan trọng khác, chúng ta cần duy trì hệ số chọn nối SFJ như thành phần của các thông tin thống kê. Trong trường hợp dó lực lượng của kết quả là:

Card (R ⋈ S) = SFJ* card(R)* card(S)

Phép nối nửa. Hệ số chọn của phép nối nửa giữa R và S cho bởi tỉ lệ phần trăm các bộ của R có nối với các bộ của S. Một xấp xỉ cho hệ số chọn của phép nối nửa được đưa ra là:

( ⋉ ) (( ))

( [ ])

Công thức này chỉ phụ thuộc vào thuộc tính A và S. Vì thế, nó thường được gọi là hệ số chọn của thuộc tính A và S, ký hiệu là SFSJ(S.A) và là hệ số chọn của

S.A trên bất kỳ một thuộc tính nào có thể nối được với nó. Vì thế, lực lượng của

nối nửa được cho bởi: Card (R ⋉ S) = SFSJ(S.A) * card(R)

Xấp xỉ này có thể được xác nhận trên một trường hợp rất thường gặp, đó là khi R.A là khóa ngoại của S (S.A là khóa chính). Trong trường hợp này, hệ số chọn nối nửa là 1 bởi vì card (πA(S)) = Card(dom[A]) cho thấy rằng lực lượng của nối nửa là card (R).

Phép hợp. Rất khó ước lực lượng trong trường hợp của R và S bởi vì các bộ giống nhau bị loại bỏ trong phép hợp. Ở đây chỉ trình bày công thức đơn giản cho các cận trên và dưới, tương ứng là:

card (R) + card (S) max{card (R), card (S)}

Trong công thức này giả thiết R và S không chứa các bộ giống nhau.

Hiệu. Giống như phép hợp, chúng ta chỉ trình bày các cận trên và dưới. Cận trên của card (R - S) là card (R), còn cận dưới là 0.

2.2.4. Tối ưu hóa cục bộ

Khi các truy vấn con được gửi đến một trạm cụ thể, nó sẽ được thực thi và tối ưu cục bộ trên trạm đó sử dụng các kỹ thuật tối ưu hóa tập trung.

2.3. Tối ưu hóa truy vấn dựa vào phương pháp tối ưu đàn kiến

Thuật toán tối ưu bầy kiến (ACO) là một thuật toán Meta - heuristic, trong đó đàn kiến nhân tạo sẽ hợp tác với nhau trong việc tìm kiếm giải pháp tốt cho các vấn đề tối ưu rời rạc khó. Quá trình hợp tác chính là chìa khóa chính để thiết kế các thành phần của thuật toán ACO: Sự lựa chọn là để cấp phát các tài nguyên tính toán cho một tập hợp các agent (tác tử) đơn giản (kiến nhân tạo) bằng phương pháp truyền thông một cách gián tiếp thông qua môi trường [6], [7].

Giải pháp tốt nổi bật đó chính là sự hợp tác để tương tác giữa các agent. Thuật toán ACO có thể sử dụng để giải quyết bài toán tối ưu tổ hợp và tối ưu tổ hợp động. Bài toán tĩnh đó chính là các đặc tính được cho trong bài toán được cho một lần và cho tất cả khi bài toán được nêu ra. Một ví dụ điển hình đó chính là bài toán tìm đường TSP (Johnson & McGeoch, 1997; Lawler, Lenstra, Rinnooy Kan & Shmoys, 1985; Reinelt, 1994). Trong đó, các thành phố và khoảng cách tương đối của chúng là một phần của định nghĩa bài toán; và không thay đổi trong suốt thời gian thực hiện. Trái lại, bài toán động thì được định nghĩa bởi một hàm mục tiêu của một vài số mà giá trị của nó sẽ thay đổi bởi một hệ thống động cơ bản. Điều đặc biệt của bài toán này là trong suốt thời gian thực hiện thì thuật toán tối ưu phải luôn thích ứng trực tuyến với sự thay đổi của môi trường. Ví dụ như bài toán về định tuyến trong mạng máy tính để điều khiển thông luồng dữ liệu, giao thức mạng có thể thay đổi theo thời gian.

ACO là một Meta-heuristic, trong đó một tập các con kiến nhân tạo phối hợp tìm kiếm các giải pháp tốt cho các vấn đề về tối ưu rời rạc. Sự phối hợp là yếu tố cối lõi của các thuật toán ACO. Các con kiến nhân tạo liên lạc với nhau thông qua trung gian mà ta thường gọi là mùi pheromone.

2.4. Một số thuật toán tối ưu hóa truy vấn phân tán

Một câu truy vấn có thể tối ưu hóa tại các thời điểm khác nhau liên quan đến thời gian thực hiện truy vấn. Việc tối ưu hóa truy vấn có thể thực hiện theo 4 phương pháp:

- Phương pháp tĩnh: Việc tối ưu hóa truy vấn tĩnh được thực hiện tại thời điểm biên dịch truy vấn. Vì vậy, chi phí truy vấn có thể được giảm dần qua nhiều lần thực hiện truy vấn, vì đây là các thời điểm thích hợp cho phương pháp tìm kiếm vét cạn. Kích thước của các quan hệ trung gian không được biết trước trước khi thực hiện. Vì vậy, cần phải được đánh giá ước lượng theo số liệu thống kê CSDL. Các sai sót trong cách đánh giá này có thể dẫn đến lựa chọn một giải pháp gần tối ưu, thuật toán tiêu biểu là R*.

- Phương pháp động: Việc tối ưu hóa động được thực hiện vào thời gian thực hiện truy vấn. Trong các thời điểm thực hiện tối ưu hóa truy vấn, việc lựa chọn thao tác tiếp theo tốt nhất cho tối ưu hóa truy vấn dựa trên những thông tin chính xác về kết quả của thao tác thực hiện trước đó. Vì vậy, các số liệu thống kê không cần thiết cho việc đánh giá kích thước của các quan hệ trung gian (nhưng có ích trong việc lựa chọn các thao tác đầu tiên). Thuật toán tiêu biểu: INGRES phân tán hay còn gọi là D-INGRES

- Phương pháp dựa trên phép nửa kết nối (semijoin): Phương pháp này sẽ sử dụng phép nửa kết nối thay cho phép kết nối để giảm kích thước của các kết quả trung gian, giảm chi phí truyền thông, từ đó giảm tổng thời gian truy vấn. Thuật toán tiêu biểu: SDD-1, AHY.

- Phương pháp tối ưu hóa truy vấn hỗn hợp có các ưu điểm của tối ưu hóa truy vấn tĩnh, tránh được các vấn đề được tạo ra bởi các đánh giá không chính xác gây ra.Về cơ bản phương pháp này là tĩnh nhưng quá trình truy vấn động có thể xảy ra lúc chạy khi phát hiện có sự khác biệt lớn giữa kích thước dự đoán và kích thước thực tế của các quan hệ trung gian. Thuật toán tối ưu truy vấn 2 pha sử dụng phương pháp này.