n
Đối với các ràng buộc aijx jbi
j1
chưa có ẩn cơ bản thì ta cộng vào vế trái
phương trình một ẩn giả xn+k 0 ( k =
1, r
với r là số ràng buộc cần thêm ẩn
giả). Trong hàm mục tiêu f(x)min hệ số của các ẩn giả xn+k là M ( với M là số lớn tùy ý, lớn hơn bất kỳ hằng số nào cần so sánh với nó) ; trong hàm mục tiêu f(x)max hệ số của các ẩn giả xn+k là -M.
Có thể bạn quan tâm!
-
Quy hoạch toán học - Ngô Hữu Tâm - 2 -
Quy Tắc Vàng Khi Lập Mô Hình Toán Học Bài Toán Thực Tế Và Khái Niệm Tối Ưu: -
Đưa Bài Toán Qhtt Dạng Chính Tắc Về Bài Toán Qhtt Dạng Chuẩn -
Định Lý 3 (Dấu Hiệu Bài Toán Có Thể Điều Chỉnh Để Được Pa Tốt Hơn) -
Quy hoạch toán học - Ngô Hữu Tâm - 7 -
Quy hoạch toán học - Ngô Hữu Tâm - 8
Xem toàn bộ 192 trang tài liệu này.
Bài toán mới có được này gọi là bài toán mở rộng, ký hiệu là (PM).
Ví dụ 6Đưa bài toán sau đây về dạng chuẩn ( bài toán ( P )): (1) f(x) = 2x1+3x2+ x3+ x4min(max)
x1
(2)
5x2
4x2
3x2
x3
5x4
6x4
8x4
25
18
28
(3) x1 0 , x2 0, x3 0, x4 0
Giải
Trước hết, ta đổi dấu hai vế của ràng buộc thứ hai. Ràng buộc thứ nhất đã có một ẩn cơ bản là x1, nên ta chỉ cần thêm ẩn giả x5vào ràng buộc thứ hai và ẩn giả x6vào ràng buộc thứ ba. Ta được bài toán mở rộng (PM) :
(1') fM (xM) = 2x1 +3x2 + x3+ x4 M(x5 +x6)min(max)
(2')
x1
5x2
4x2
x3
5x4
6x4
x5
25
18
3x2
8x4
x6 28
(3') x1 0 , x2 0, x3 0, x4 0, x5 0, x6 0
Ví dụ 7Đưa bài toán sau đây về dạng chuẩn ( bài toán ( P )):
n
(1) f(x) = c jx j
j1
min ( max)
n
(2) aijx jbi
j1
, với bi 0 ( i = 1, m )
(3) xj 0 , j = 1, 2, …, n
Giải
Cộng vào vế trái mỗi ràng buộc ở (2) một ẩn giả ta được ta được bài tốn mở rộng
n
(PM): (1’) fM(xM) = c jx j
j1
M(xn+1 +...+xn+m)min ( max)
n
(2’) aijx j+ xn+k bi
j1
, với bi 0 ( i = 1, m , k =1, m )
(3’) xj 0 , j = 1, 2, …, n, n+1,..., n+m.
Nhận xét:
i) Nếu x = (x1,..., xn) là phương án của bài toán ( P ) thì xM= (x1,...,xn,0,...,0) là phương án của bài toán mở rộng (PM).
ii) Nếu x*= ( x*,..., x*,0,...,0) là PATƯ của bài toán mở rộng (PM) thì
M 1 n
x*= ( x*,..., x*) là PATƯ của bài tốn ( P ). Ngược lại, nếu x*= ( x*,..., x*) là
1 n 1 n
PATƯ của bài toán ( P ) thì x*= ( x*,..., x*,0,...,0) là PATƯ của bài toán mở
M 1 n
rộng (PM). Suy ra, nếu (PM) không có PATƯ thì ( P ) có cũng không có PATƯ.
iii) Nếu (PM) có PATƯ x* = ( x* ,..., x* , x*
,..., x*
), với ít nhất một ẩn giả
M 1 n
n1
nm
x
* nk
> 0 thì ( P ) không có PA. Thật vậy, giả sử ngược lại ( P ) có PA là
M
x = (x1,..., xn). Khi đó (PM) có PA là xM= (x1,...,xn,0,...,0); hơn nữa vì M lớn
x
tùy ý và
* nk
> 0 nên fM(xM) < fM( x*
) đối với trường hợp fmin và fM(xM)
M
> fM( x*) đối với trường hợp fmax . Điều này vô lý với tính chất tối ưu của
x
.
* M
Kết luận
Bất kỳ bài toán QHTT dạng chính tắc nào cũng đưa được về bài toán QHTT dạng chuẩn.
Nếu bài toán mở rộng (PM) không có PATƯ thì bài toán ( P ) không có PATƯ.
Nếu bài toán mở rộng (PM) có PATƯ và tất cả các ẩn giả đều bằng 0 thì bỏ phần ẩn giả ta được PATƯ của bài tốn ( P ).
Nếu bài toán mở rộng (PM) có PATƯ và ít nhất một ẩn giả khác 0 thì bài toán ( P ) không có PA và do đó không có PATƯ.
Tóm lại, mọi bài toán QHTT dạng tổng quát đều có thể đưa về bài toán QHTT dạng chính tắc; mọi bài toán QHTT dạng chính tắc đều có thể đưa về bài toán QHTT dạng chuẩn. Như vậy, ta chỉ cần giải bài toán dạng chuẩn.
2.4. Các tính chất bài toán QHTT
Ta đã biết, mọi bài toán QHTT tổng quát (P) đều có thể đưa về bài toán QHTT dạng chính tắc ( P ) tương ứng; và bài toán (P) có PATƯ khi và chỉ khi bài toán ( P ) có PATƯ. Do đó, ta chỉ cần xét tính chất của bài toán QHTT dạng chính tắc. Không mất tính tổng quát, ta có thể giả thiết m ràng buộc độc lập tuyến tính và m < n. Nếu thêm giả thiết hệ phương trình ràng buộc có nghiệm thì ta có thể dùng phép khử Gauss-Jordan để biến đổi tương đương hệ đó về hệ phương trình chuẩn. Khi đó ta có các tính chất quan trọng sau đây của bài toán QHTT dạng chính tắc:
Tính chất 1: (sự tồn tại phương án)
Nếu bài toán có phương án thì có phương án cơ bản.
Tính chất 2: (sự tồn tại phương án tối ưu)
Nếu bài toán có phương án tối ưu thì có phương án cơ bản tối ưu.
Tính chất 3: (tính hữu hạn của số phương án )
Số phương án cơ bản khác nhau trong mỗi bài toán là hữu hạn.
.............................................................................................................
Bài tập
Bài 1.19 Trong các bài toán từ 1 đến 6 dưới đây: 1. (1) f(x) = 2x1+3x2+ x3+ x4max
x1
(2)
x1
x2
x2
x2
2x3
x3
2x3
x4
2x4
x4
x5
32
16
32
(3) x1, x3 0; x2 0; x4, x5 tùy ý
2. (1) f(x) = 2x1 +3x2 + x3+ x4 min
2x1
(2) 4x
x2
2x
3x3
x
4x5
5x
17
20
1 3 4 5
2x1 4x5 x6 6
(3) xj 0 (j = 1,6 )
3. (1) f(x) = 2x1 +3x2 + x3+ x4 max
x1
(2) x
x2
2x
2x3
x x
5
15
1 2 3 4
2x1 x2 3x3 8
(3) xj 0 (j = 1,4 )
4. (1) f(x) = 2x1 +3x2 + x3+ x4 min
x1
(2) x
2x2
2x
2x3
x
7
15
2 3 4
2x1 3x3 x4 8
(3) xj 0 (j = 1,4 )
5.
(1) f(x) = - 2x1 + x2 + x4 min
x1
(2) x
x2
x
x3
x x
15
27
1 2 3 4
2x1 x2 x3
18
(3) xj 0 (j = 1,4 )
6.
(1) f(x) = x1 + 2x2 – x3 max
4x1
(2) x
4x 2
x
2x3
2x
6
6
1 2 3
2x1 x 2 2x3 4
(3) xj 0 ( j = 1,3 )
a) Những bài toán nào đã có dạng chính tắc?
b) Những bài toán nào có dạng chuẩn? Nếu bài toán có dạng chuẩn thì hãy chỉ ra các ẩn cơ bản và thứ tự của chúng? Hãy tìm phương án cơ bản ban đầu của nó.
c) Bài toán nào chưa có dạng chuẩn hãy đưa về dạng chuẩn sau đó cho biết ẩn nào là ẩn cơ bản, ẩn cơ bản ấy là ẩn gì (ẩn chính? ẩn phụ? ẩn giả? ), thứ tự của nó thế nào? Phương án cơ bản ban đầu của bài toán dạng chuẩn này thế nào?
Đ 3. PHƯƠNG PHÁP HèNH HỌC
3.1. Một số kết quả trong hình học
Đường thẳng ax + by = c chia mặt phẳng Oxy ra thành hai miền: Một miền gồm tất cả các điểm (x,y) thỏa mãn bất phương trình ax + by > c; một miền gồm tất cả các điểm (x,y) thỏa mãn bất phương trình ax + by < c. Như vậy, mỗi bất phương trình dạng ax + by c ( hoặc ax + by c, với điều kiện a2+b20) xác định một nửa mặt phẳng kín.
Họ đường thẳng ax + by = m ( m ) là tập hợp các đường thẳng song song với nhau, mà ta gọi là các đường mức ( tương ứng với mức m ). Nếu ta tịnh tiến một
đường thẳng trong họ ( một đường mức) theo hướng vectơ n = (a;b) thì giá trị
tương ứng của m tăng, còn theo hướng ngược lại thì giá trị tương ứng của m giảm.
3.2. Các bước giải bài toán QHTT hai biến bằng phương pháp hình học
Giải bài toán : f(x) = c1x1+ c2x2min ( max) (1)
a x a x
b , i 1, m
(2)
D:
i1 1
i2 2 i
x10 , x20 (hoặc
a x1 b , c x2 d)
(3)
Bước 1Vẽ miền ràng buộc D trong mặt phẳng Ox1x2.
Bước 2Xác định điểm C(c1,c2); vẽ OC hoặc vectơ đơn vị
n cùng chiều OC =
(c1,c2); vẽ tùy ý một đường mức (d) n và cắt miền phương án D.
Bước 3
Để tìm phương án tối ưu đối với bài toán fmax , ta tịnh tiến đường mức (d)
theo hướng véctơ n đến khi việc tịnh tiến tiếp theo làm cho đường mức không
còn điểm chung với D nữa thì dừng. Điểm thuộc D nằm trên đường mức cuối cùng này ( đây là điểm tiếp xúc của (d) với D và có thể có nhiều điểm) là PATƯ và giá trị hàm mục tiêu tại điểm đó là giá trị tối ưu của bài toán.
Để tìm phương án tối ưu đối với bài toán fmin , ta tịnh tiến đường mức (d)
theo hướng ngược lại với véctơ n đến khi việc tịnh tiến tiếp theo làm cho
đường mức không còn điểm chung với D nữa thì dừng. Điểm thuộc D nằm trên đường mức cuối cùng này ( đây là điểm tiếp xúc của (d) với D và có thể có nhiều điểm) là PATƯ và giá trị hàm mục tiêu tại điểm đó là giá trị tối ưu của bài toán.
Nếu tịnh tiến (d) mãi mà không tìm được vị trí tiếp xúc của (d) với D thì kết luận bài toán không có PATƯ và hàm mục tiêu không bị chặn trên miền PA (f-, đối với bài toán min; f +, đối với bài toán max).
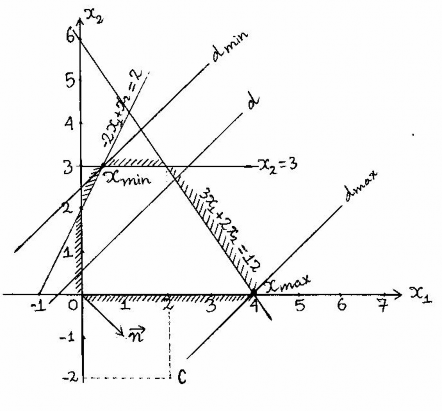
Ví dụ 1Giải bài toán QHTT sau đây bằng phương pháp hình học. f(x) = 2x1-2x2min ( max)
D:
3x1 2x2 12
- 2x1 x2 2
x10 , x20,
x2 3
Giải
Miền phương án D, đường mức (d), điểm C và vectơ n được xác định như hình vẽ.
Trường hợp fmax: Tịnh tiến (d) theo hướng n ta được dmax và từ đó tính được xmax = (4;0) , fmax = 8.
Trường hợp fmin: Tịnh tiến (d) theo hướng ngược lại với đó tính được xmin = ( 1;3) , fmin = -5.
2
n ta được dmin và từ
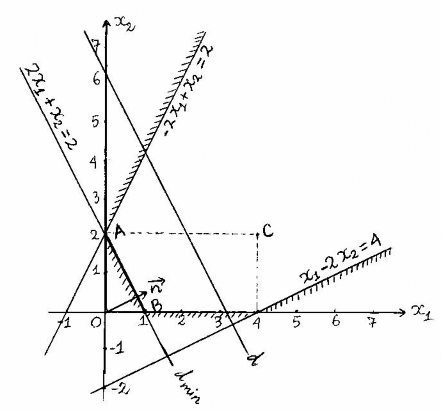
Ví dụ 2Giải bài toán QHTT sau đây bằng phương pháp hình học.
f(x) = 4x1 +2x2 min ( max)
2x1 x2 2
x1 2x2 4
D: - 2x1 x2 2
x10 , x20
Giải
Miền phương án D, đường mức (d), điểm C và vectơ n được xác định như hình vẽ.
Trường hợp fmin: Tịnh tiến (d) theo hướng ngược lại với
n ta được dmin và từ
đó tính được xmin = (t; 2-2t) với 0 t 1, fmin = 4. Tức là, PATƯ ứng với trường hợp fmin là cả đoạn thẳng AB.
Trường hợp fmax: Tịnh tiến (d) theo hướng
n ta thấy (d) và D không có điểm
tiếp xúc. Tức là, hàm mục tiêu không bị chặn trên và bài toán không có phương án tối ưu.
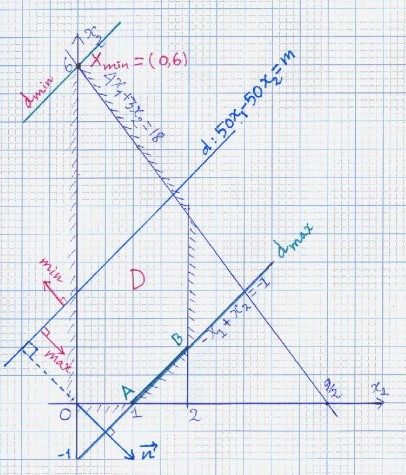
Ví dụ 3Giải bài toán QHTT sau đây bằng phương pháp hình học. f(x) = 50x1- 50x2min (max)
D:
4x1 3x2 18
- x1 x2 1
x1 0 , x 2 0,
x1 2
Giải
Miền phương án D, véc tơ n (1;1) OC (50;50) , đường mức (d ) như hình vẽ.
Trường hợp fmin: Tịnh tiến (d) theo hướng ngược lại với n ta được dmin và
từ đó tính được X min (0;6) , f min f (0,6) 300 .
Trường hợp fmax: Tịnh tiến (d) theo hướng
n ta được dmax và từ đó tính
được
X max
là tập hợp tất cả các điểm thuộc đoạn AB như hình vẽ. Tính được
X max (1 t;t)
với
0 t 1 và
f max
f (1 t, t) 50(1 t) 50t 50 .
Bài tập
Giải các bài tập toán QHTT sau đây bằng phương pháp hình học.
Bài 1.20f(x) = x1 + x2 min (max)
3x1
3x
2x2 6
x 3
1 2
x1 3
Bài 1.21f(x) = x1 + 2x2 min (max)
x1
x
8x2
x
10
1
1 2
x1 5x2
3x110x2
5
30
Bài 1.22f(x) = -2x1 + x2 min (max)
x1 x2 1
x1 2x2 4
2x1
x2 6
4x1 x2 20
x10 ; x20