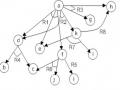
(16), (6) suy ra C (17)
(17), (11) suy ra câu , vậy C được chứng minh
Bài 3.14.
Chuẩn hóa về dạng chuẩn hội ((BC) (GE)) (AD C)
((BC) (GE)) ((AD) C)
(BC) (GE)) ((AD) C)
(BG) (BE) (CG) (CE))
((AD) C)
(BG) (BE) (CG) (CE)
(AC) (D C) D BE DBE ADC ADC A: đã được chuẩn hóa Chứng minh công thức
Có thể bạn quan tâm!
-
Nhập môn trí tuệ nhân tạo - 28 -
Nhập môn trí tuệ nhân tạo - 29 -
Nhập môn trí tuệ nhân tạo - 30 -
Nhập môn trí tuệ nhân tạo - 32 -
Nhập môn trí tuệ nhân tạo - 33
Xem toàn bộ 272 trang tài liệu này.
- Thành lập các câu tuyển
BG (1)
BE (2)
CG (3)
CE (4)
AC (6)
D C (7)
DBE (8)
ADC (9)
A (10)
- Chứng minh diễn dịch (10), (6) suy ra C (11) (11), (3) suy ra G
- Chứng minh phản chứng
- Bổ sung G (12) (12), (3) suy ra C (13)
(13), (6) suy ra A (14)
(14), (10) suy ra câu rỗng
vậy G được chứng minh
Bài 3.15.
Chứng minh bằng phương pháp diễn dịch
(A B D) (B C F) suy ra A B D, B C F (CD) (D E) suy ra CD, D E
E, D E suy ra D D, CD suy ra C
C suy ra CF
CF (CF)
(CF), B C F suy ra B
B BD
BD(BD)
A B D, (BD) suy ra A Chứng minh bằng phản chứng Bổ sung A
A, A B D suy ra B D B D suy ra B
B, B CF suy ra CF CF suy ra C
C, CD suy ra D
D, D E suy ra E E, E suy ra câu Bài 3.16
Chuẩn hóa về dạng chuẩn hội và thành lập các câu tuyển Chuẩn hóa về dạng chuẩn hội
A (B E) A(BE) ABE C (D P) CDP
(E C) (P Q) (EC) (PQ) Thành lập các câu tuyển
ABE (1)
CDP (2)
A (5)
B (6)
D (7)
EC (3)
PQ (4)
Chứng minh công thức
a) Sử dụng phương pháp chứng minh diễn dịch (1), (5), (6) suy ra E (8)
(8), (3) suy ra C (9)
(9), (7), (2) suy ra P (10)
(10), (4) suy ra Q
b) Sử dụng phương pháp chứng minh phản chứng. Bổ sung Q (11)
(11), (4) suy ra P (12)
(12), (2) suy ra CD (13)
(13), (7) suy ra C (14)
(14), (3) suy ra E(15)
(15), (1) suy ra AB (16)
(16), (5), (6) suy ra câu Kết luận Q được chứng minh Bài 3.17.
Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển Chuẩn hóa về dạng chuẩn hội
B (A C) (BAC) (BCA) C (D P) (CDP) (CPD) A, B, D đã chuẩn hóa
Thành lập câu tuyển
BAC
BCA
CDP
CPD A
B D
Chứng minh công thức
a) Sử dụng phương pháp chứng minh diễn dịch A, B, BAC suy ra C
C, D, CDP suy ra P
b) Sử dụng phương pháp chứng minh phản chứng Bổ sung P
P, CDP suy ra CD
CD, D suy ra C
C, BAC suy ra BA
BA, A, B suy ra câu Vậy D được chứng minh Bài 3.18.
Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển Chuẩn hóa về dạng chuẩn hội
AD BC ((AD) (BC)) ((BC) (AD))
(ABC) (DBC) (BAD) (CAD) AC AC
B D B D Thành lập câu tuyển
ABC DBC
BAD
CAD
AC
BD A
Chứng minh công thức
a) Sử dụng phương pháp chứng minh diễn dịch
ABC, AC suy ra AB
AB, A suy ra B
b) Sử dụng phương pháp chứng minh phản chứng Bổ sung B
B, ABC suy ra AC
AC, AC suy ra A
A, A suy ra câu
Vậy B được chứng minh
Bài 3.19.
Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển Chuẩn hóa về dạng chuẩn hội
(A(BC)) (DE) (A(BC)) (DE)
(AB) (AC)) (DE)
(A B) C ((A B) C) ((B A) C)
(ABC) (BAC) Thành lập câu tuyển
AB
AC DE
ABC
BAC
Chứng minh công thức
a) Sử dụng phương pháp chứng minh diễn dịch
AB, ABC suy ra AC
AC, AC suy ra A
b) Sử dụng phương pháp chứng minh phản chứng Bổ sung A
A, AB suy ra B
B, ABC suy ra AC
AC, AC suy ra A
A, A suy ra câu
Vậy A được chứng minh
Bài 3.20.
Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển Chuẩn hóa về dạng chuẩn hội
(A(BC)) D (A (BC)) D
(A (BC)) D(A(BC)) D
(A D) (BCD)
(B C) E(BC) E(BC) E
(B E) (CE) DBE(DB) E
(DB) E(DE) (BE) Thành lập câu tuyển
A D
BCD B E
CE
DE BE
Chứng minh công thức
a) Sử dụng phương pháp chứng minh diễn dịch B E, BE suy ra B
B, BCD suy ra CD
CD, DE suy ra CE
CE, CE suy ra C
b) Sử dụng phương pháp chứng minh phản chứng Bổ sung C
C, BCD suy ra BD B E, BE suy ra B
B, BD suy ra D D, DE suy ra E
E, CE suy ra C
C, C suy ra câu vậy C được chứng minh
3.30. Hướng dẫn
Ký hiệu a: cạnh a của tam giác k: đường cao tương ứng với cạnh a b: cạnh b của tam giác l: đường cao tương ứng với cạnh b c: cạnh c của tam giác m: đường cao tương ứng với cạnh c A: góc tương ứng với cạnh a S: diện tích của tam giác
B: góc tương ứng với cạnh b p: nữa chu vi của tam giác C: góc tương ứng với cạnh c
- Các tri thức đó được biểu diễn dưới dạng logic mệnh đề như sau:
1) abc p
2) bpc a
3) apc b
4) abp c
5) Sa k
6) Sb l
7) Sc m
8) abC c
9) acB b
10) bcA a
11) abC S
12) acB S
13) bcA S
14) abcp S
15) Sk a
16) Sl b
17) Sm c
3. Bài tập Chương 4 Bài 4.9.
1.Chuyển các câu sang logic vị từ
- Khai báo
+ Hằng: Bình, Huy, Mai, An, Nam Định, Thái Bình
+ Vị từ:
que (x, y) ="x quê ở y”
Ban (x, y) ="x là bạn của y và ngược lại”
- Chuyến sang logic vị từ
x (que(x, Nam Định) que(x, Thái Bình))
y (Ban(y, Bình) que(y, Nam Định))
Ban(Mai, Bình) Ban(Mai, Huy)
(que(An, Nam Định) que(Huy, Nam Định)) (que(An, Thái Bình) que(Huy, Thái Bình)) ban(An, Bình)
2.Chứng minh quê của An, Huy đều ở Thái Bình
- Chuẩn hóa
que(x, Nam Định) que(x, Thái Bình) (1)
Ban(y, Bình) que(y, Nam Định) (2)
Ban(Mai, Bình) (3)
Ban(Mai, Huy) (4)
que(An, Nam Định) que(Huy, Nam Định) (5)
que(An, Thái Bình) que(Huy, Thái Bình) (6) ban(An, Bình) (8)
- Xét An
(8), (2) suy ra que(An, Nam Định) (9)
(9), (1) suy ra que(An, Thái Bình) (10)
- Xét Huy
(11), (6) suy ra que(Huy, Thái Bình)
Bài 4.10.
1.Biểu diễn câu trong logic vị từ
- Khai báo
+ Hằng: Huy, Mai, An, Bình, chồng Mai, vợ Bình
+ Vị từ: