F F1 F2 F F1 F2
F fN1 fN2
F 2 fN1
(4.3)
Từ (4.2) và (4.3) suy ra
F f N
Có thể bạn quan tâm!
-
Số Liệu Cho Trước, Giả Thiết Và Nội Dung Của Bài Toán Phân Tích Lực Cơ Cấu -
Điều Kiện Tĩnh Định Của Bài Toán Phân Tích Áp Lực Khớp Động -
Hiện Tượng Có Chuyển Động Tương Đối -
Tổng Phản Lực Và Tổng Lực Ma Sát Trong Khớp Quay -
Các Dạng Hỏng Của Mối Ghép Và Chỉ Tiêu Tính Toán -
Trị Số Ứng Suất Cho Phép Dùng Cho Tính Toán Mối Ghép Bằng Đinh Tán
Xem toàn bộ 167 trang tài liệu này.
sin
Hay
F f '.N
(4.4)
Với
f '
f
sin
(4.5)
f’ được gọi là hệ số ma sát thay thế.
+ Như vậy, ma sát trong rãnh hình tam giác có thể quy về ma sát trên mặt phẳng bằng cách sử dụng hệ số ma sát thay thế f’. Biểu thức (4.5) cho thấy ma sát trong rãnh hình tam giác lớn hơn ma sát trên mặt phẳng.
4.2.2. Ma sát trên mặt phẳng nghiêng
Xét vật A nằm trên mặt phẳng nghiêng B. Vật A tiếp xúc với B theo mặt phẳng
Q
và chịu tác động của một lực thẳng đứng. Gọi α là góc nghiêng của mặt phẳng. Gọi
f là hệ số ma sát trượt, υ là góc ma sát với tgυ = f.
Q
Q
+ Khi α < υ thì nằm trong nón ma sát (hình 4.9a) và vật A bị tự hãm khi đi
xuống (dù
có giá trị lớn bao nhiêu đi nữa, vật A vẫn không thể đi xuống trên mặt
phẳng nghiêng).
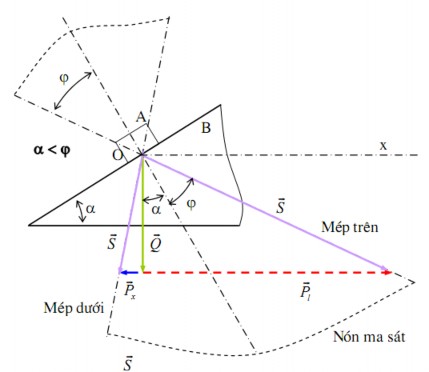
Hình 4.9a. Hiện tượng tự hãm
P
Để cho vật A đi lên đều hay đi xuống đều, phải tác động lên A một lực đẩy so
S P Q
Q
cho hợp lực nằm trên mép trên hay mép dưới của nón ma sát.
P
Giả sử lực đẩy ta suy được:
có phương nằm ngang (vuông góc với ). Dựa trên hình 4.9a,
- Để A đi lên đều:
PP1Qtg
- Để A đi xuống đều:
P Px Qtg
Q
dần.
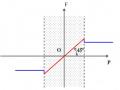
+ Khi α > υ (hình 4.9b) thì
nằm ngoài nón ma sát (N) và vật A đi xuống nhanh
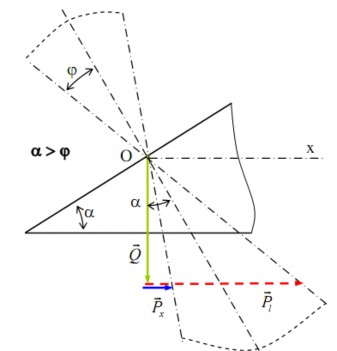
Hình 4.9b. Hiện tượng trượt nhanh dần
Tương tự như trên, ta có:
- Để A đi lên đều:
PP1Qtg
- Để A đi xuống đều:
P Px Qtg
+ Trong cả hai trường hợp trên, nếu
2
thì mép trên của nón ma sát nằm
phía trên đường thẳng nằm ngang Ox (hình 4.9a, b). Khi đó dù giá trị của lực P có lớn
S P Q
bao nhiêu đi nữa thì hợp lực: cũng không thể vượt ra ngoài mép trên của nón
ma sát: A bị tự hãm khi đi lên.
4.2.3. Ma sát trên rãnh nghiêng hình tam giác
+ Xét vật A nằm trên rãnh nghiêng hình tam giác B (hình 4.10a).
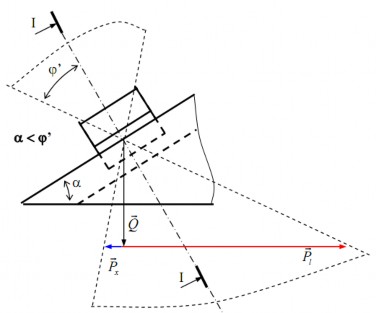
Hình 4.10a. Hiện tượng tự hãm
Hình 4.10b mô tả mặt cắt ngang của rãnh nghiêng, 2γ là góc nhị diện của rãnh nghiêng. Gọi α là góc nghiêng của phương trượt của rãnh nghiêng so với mặt phẳng
Q
nằm ngang, υ là góc ma sát. Giả sử vật A chịu tác động của lực thẳng đứng.
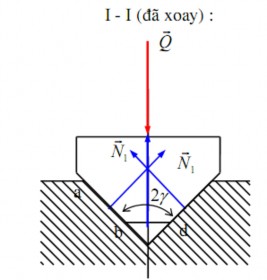
Hình 4.10b. Phản lực trong rãnh tam giác
+ Tương tự như trên, có thể quy trường hợp ma sát trên rãnh nghiêng hình tam giác về trường hợp ma sát trên mặt phẳng nghiêng, bằng cách thay thế hệ số ma sát f
bằng hệ số ma sát thay thế
với tgυ’=f’.
f '
f
sin
, thay góc ma sát υ bằng góc ma sát thay thế υ’
Lực đẩy nằm ngang để vật đi lên hay đi xuống đều cũng như điều kiện tự hãm khi vật đi lên hay đi xuống trên rãnh nghiêng được suy luận tương tự như trường hợp vật đi lên hay đi xuống trên mặt phẳng nghiêng:
- Khi α < υ’ thì vật A bị tự hãm khi đi xuống trên rãnh nghiêng.
- Lực đẩy nằm ngang P để vật A đi lên hay đi xuống đều trên rãnh nghiêng:
Khi' : P P1Qtg ';P PxQtg '
Khi' : P P1Qtg ';P PxQtg '
- Khi '
2
thì vật A bị tự hãm khi đi lên.
4.2.4. Ma sát trong khớp ren vít
a. Cấu tạo của khớp ren vít
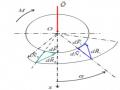
Cho hình trụ (Γ) và đường xoắn ốc trên (Γ) có góc xoắn là α. (M) là mặt phẳng đi qua trục zz của hình trụ. Đặt trên (M) một hình chữ nhật abcd, cạnh ad nằm trên một đường sinh của hình trụ, đỉnh a nằm trên đường xoắn ốc.
Cho (M) quay quanh trục z và luôn giữ cho a chạy trên đường xoắn ốc thì khi đó các cạnh ab, cd của hình chữ nhật sẽ vạch nên những mặt gọi là mặt ren vuông (hình 4.11).
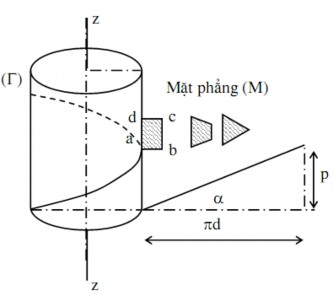
Hình 4.11. Nguyên lý tạo ren
+ Nếu thay hình chữ nhật abcd bằng hình thang hay hình tam giác thì mặt ren được tạo ra sẽ là mặt ren thang hay mặt ren tam giác.
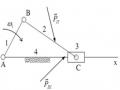
+ Khớp ren vít gồm có hai khâu: đai ốc có ren trong và vít có ren ngoài (hình 4.12a, 4.12b).
Khớp ren vuông (hình 4.12a), khớp ren hình thang dùng để biến chuyển động quay thành chuyển động tịnh tiến trong kích vít, trong có cơ cấu vít me – đai ốc. Khớp ren hình tam giác (hình 4.12b) thường dùng trong các mối ghép dùng để ghép chặt các chi tiết máy với nhau.
Hình 4.12a. Khớp ren vuông
b. Ma sát trong khớp ren vuông
Q
+ Gọi là tải trọng dọc trục (thẳng đứng) đặt lên đai ốc A. Ta cần tính mô men
Mr cần thiết để vặn cho đai ốc đi lên (vặn vào) hay đi xuống (nới ra) trên vít (hình 4.12a)
+ Ma sát trong khớp ren vuông có thể xem như ma sát trên mặt phẳng nghiêng, góc nghiêng của mặt phẳng là góc xoắn α của đường xoắn ốc.
+ Việc vặn đai ốc vào hay nới lỏng đai ốc ra bằng cách tác động lên đai ốc mô
P
men Mr tương đương với việc đai ốc đi lên hay đi xuống đều trên mặt phẳng nghiêng nhờ một lực đẩy lực đẩy nằm ngang :
P Qtg()
trong đó:
M r P.rtb .
Suy ra mô men để vặn đai ốc vào hay nới lỏng đai ốc là:
M r Q.rtbtg
+ Việc đai ốc không tự nới lỏng ra dù giá trị của lực
có lớn đến bao nhiêu đi
Q
nữa tương đương với việc đai ốc bị tự hãm khi đi xuống trên mặt phẳng nghiêng, tức là khi: α < υ.
c. Ma sát trong khớp ren hình tam giác
Gọi β là nửa góc ở đỉnh của hình tam giác (β còn được gọi là góc tiết diện ren). Ma sát trong khớp ren tam giác có thể xem như ma sát trên rãnh nghiêng hình tam giác với góc nghiêng của phương trượt của rãnh nghiêng bằng góc xoắn α của đường xoắn
ốc, góc nhị diện của rãnh bằng 2γ (hình 4.12b) với
.
2
Lý luận tương tự như trường hợp ma sát trong khớp ren vuông, ta có:
- Mô men để vặn đai ốc vào hay nới lỏng đai ốc:
M r rtb .Qtg '
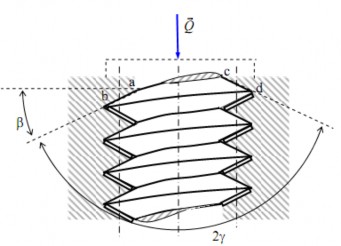
Hình 4.12b. Khớp ren tam giác
Với υ’ là góc ma sát thay thế
tg' f '
. f’ là hệ số ma sát thay thế:
f '
f
sin
hay f '
f cos
Q
- Điều kiện để đai ốc không tự nới lỏng ra dù giá trị của lực nhiêu đi nữa: '
có lớn đến bao
4.3. Ma sát trượt trong khớp quay
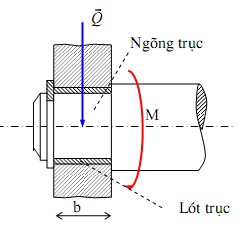
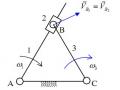
Hình 4.13a. Khớp quay
Trong khớp quay có hai khâu được nối với nhau là trục và ổ trục. Chi tiết trong ổ trục trực tiếp tiếp xúc với trục là lót trục (hình 4.13a).
Phần trục trực tiếp tiếp xúc với lót trục được gọi là ngòng trục. Hình 4.13b mô tả một mặt cắt ngang của khớp quay. Ta sẽ sử dụng mặt cắt ngang này để nghiên cứu bài toán.
4.3.1. Mô men ma sát trong khớp quay
Q
+ Giả sử trục quay đều dưới tác dụng của tải trọng
thẳng đứng qua tâm O của
trục và mô men M nằm trong mặt phẳng vuông góc với trục quay (hình 4.13b). Trục và lót trục tiếp xúc theo cung tròn AB = β. Giả sử áp suất từ lót trục tác dụng lên ngòng trục phân bố theo quy luật p(α) nào đó trong cung tiếp xúc AB. Hãy xác định mô men ma sát MMS trong khớp quay.
B
A
Hình 4.13b. Phân bố phản lực trong khớp quay
+ Xét phân tố diện tích tiếp xúc dS, chắn cung dα. Vị trí của dS được xác định
Q
bằng góc α so với phương của lực (so với trục Ox). Chiều dương của trục Ox và
chiều dương để xác định các góc định hướng như trên hình 4.13b. Ta có:
dS = brdα
Với r là bán kính ngòng trục, b là chiều dài tiếp xúc giữa lót trục và ngòng trục.
N
+ Trên dS phản lực từ lót trục tác dụng lên ngòng trục là d . Do dS khá nhỏ nên
có thể xem như áp suất phân bố đều trên dS và có giá trị bằng p(α). Do đó:
dN p dS brp d
dN
Do các áp suất p(α) đều đi qua tâm O của trục nên phản lực
cũng đi qua tâm O.
+ Khi trục quay, trên dS xuất hiện lực ma sát
có chiều hướng ngược với
dF
chiều quay của trục. Cũng do dS khá nhỏ nên có thể xem dS là một mặt phẳng, theo định luật Coulomb ta có:
F N
d d và dF=fdN=brfpd
Với f là hệ số ma sát trượt.
+ Mô men ma sát trên phân tố diện tích dS:
2
dM MS rdF bfr p d
Suy ra mô men ma sát từ lót trục tác dụng lên ngòng trục:
MMS
dMMSbfr p d
2
MMS
bfr2
p d
(4.6)
* Công thức (4.6) mới chỉ cho ta quan hệ giữa mô men ma sát MMS và áp suất
Q
Q
R N F
p(α). Để tính MMS theo tải tọng cần xác định quan hệ giữa và p(α).
dN 2 dF 2
dN 2fdN2
1f 2
Gọi:
d d d
Ta có:
dR
dN
dR br
1f 2 p d
dF
Và: tg d R, d N f
dN
tg
(hình 4.14a)
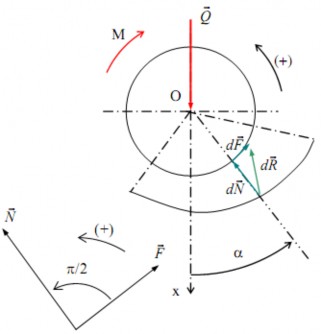
R N
d , d
Hình 4.14a. Quan hệ mômen ma sát và áp suất