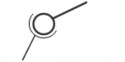
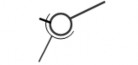
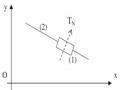
Số bậc tự do tương đối bị hạn chế đi là 2 (hai chuyển động Qy, Tz không thể xảy ra vì khi đó hình trụ không còn tiếp xúc với tấm phẳng theo đường sinh nữa). Khớp động này là khớp loại 2. Thành phần khớp động trên khâu 1 là đường sinh AA’ của nó hiện đang tiếp xúc với mặt phẳng của khâu 2. Thành phần khớp động trên khâu 2 là đoạn thẳng BB’ hiện trùng với đường sinh AA’. Thành phần khớp động là các đường nên khớp động này là một khớp cao.
+ Ví dụ 2:
Hình cầu tiếp xúc với nhau ( hình 1.7) cho ta một khớp động. Số bậc tự do tương đối bị hạn chế đi là 3 (hạn chế ba chuyển động Tx, Ty, Tz), nên đây là một khớp cầu loại 3. Thành phần khớp động là các mặt cầu, vậy khớp cầu nói trên là một khớp thấp.
Hình 1.7. Khớp cầu
+ Ví dụ 3:
Hình 1.8. Khớp cầu có chốt
Khớp cầu có chốt (hình 1.8). Khác với khớp cầu loại 3 trên đây, trên khâu 2 của khớp cầu này có gắn thêm chốt 3, trên khâu 1 có xẻ rãnh 4. Khi đó, khâu hai chỉ còn hai khả năng chuyển động tương đối so với khâu1: chuyển động quay Qx xung quanh trục x và chuyển động quay Qy xung quanh trục y. Khớp này hạn chế 4 bậc tự do tương đối, do vậy là khớp loại 4. Thành phần khớp động là các mặt cầu nên đây là một khớp thấp.
+ Ví dụ 4:
Khớp tịnh tiến ( khớp trượt – hình 1.9): số bậc tự do tương đối bị hạn chế đi là 5 (chỉ để lại chuyển động tịnh tiến Tx) nên khớp trượt là khớp loại 5. Thành phần khớp động là các mặt phẳng, nên khớp trượt là một khớp thấp.
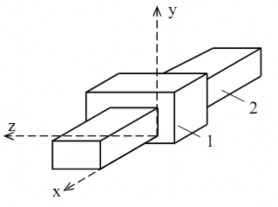
Hình 1.9. Khớp trượt
+ Ví dụ 5:
Khớp quay (khớp bản lề - hình 1.10): số bậc tự do tương đối bị hạn chế đi là 5 (chỉ để lại chuyển động quay Qz) nên khớp quay là một khớp loại 5. Thành phần khớp động là các mặt trụ tròn xoay A và các phần mặt phẳng B, nên đây là một khớp thấp.
Hình 1.10. Khớp quay
+ Ví dụ 6
Khớp vít (ví dụ vít me – đai ốc hình 1.11): khâu 1 có hai khả năng chuyển động tương đối so với khâu 2, đó là hai chuyển động Tz và Qz. Tuy nhiên hai khả năng chuyển động này phụ thuộc lẫn nhau ( khi giữ vít me cố định và xoay đai ốc một góc nào đó quanh trục Oz thì đai ốc sẽ tịnh tiến một khoảng xác định dọc theo trục Oz). Do vậy khớp vít là khớp loại 5. Thành phần khớp động là các mặt ren vít nên đây là một khớp thấp.
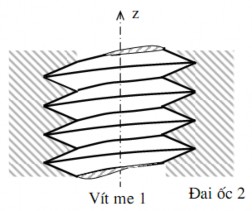
Hình 1.11. Khớp vít
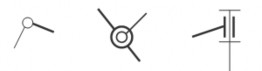
c. Lược đồ khớp
Trên thực tế, kết cấu khâu và khớp rất phức tạp. Để thuận tiện cho việc nghiên cứu các bài toán về cơ cấu, người ta biểu diễn các khớp động khác nhau bằng các lược đồ quy ước. Lược đồ một số khớp thông dụng:
| |
Khớp cầu có chốt (Khớp thấp, loại 4) |
|
Khớp tịnh tiến (Khớp thấp, loại 5) |
|
Khớp bản lề (Khớp thấp, loại 5) |
|
Khớp vít (Khớp thấp, loại 5) |
|
Khớp cao phẳng (khớp bánh răng phẳng, khớp cam phẳng…) (Khớp cao, loại 4) |
|
Có thể bạn quan tâm!
-
 Nguyên lý chi tiết máy 1 - 1
Nguyên lý chi tiết máy 1 - 1 -
 Công Thức Tính Bậc Tự Do Của Cơ Cấu Phẳng
Công Thức Tính Bậc Tự Do Của Cơ Cấu Phẳng -
 Họa Đồ Chuyển Vị Của Cơ Cấu Và Đồ Thị Chuyển Vị S(Φ)
Họa Đồ Chuyển Vị Của Cơ Cấu Và Đồ Thị Chuyển Vị S(Φ) -
 Nguyên lý chi tiết máy 1 - 5
Nguyên lý chi tiết máy 1 - 5
Xem toàn bộ 167 trang tài liệu này.
1.1.4. Kích thước động của khâu và lược đồ khâu
Kích thước động của khâu là các thông số xác định vị trí tương đối giữa các thành phần khớp động trên khâu.
Ví dụ 1:
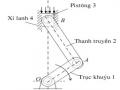
Thanh truyền (2) trong động cơ đốt trong (hình 1.1) được nối với tay quay (1) và với pistông (3) bằng các khớp quay, các thành phần khớp động trên thanh truyền là các mặt trụ trong có đường trục song song với nhau. Kích thước động của thanh truyền là khoảng cách li giữa hai đường trục của các khớp quay.
Mỗi khâu có thể có một hay nhiều kích thước động.
Ví dụ 2:
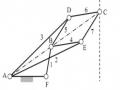
Khâu 3 trên hình 1.14 được nối động với ba khâu 6, 2 và 4 bằng các khớp quay D, C, E. Khâu 3 có ba kích thước động, đó là khoảng cách trục lEC, lDE, lDC giữa các khớp quay.
Khâu được biểu diễn bằng các lược đồ gọi là lược đồ động của khâu, trên đó trể hiện các kích thước động của nó và lược đồ các khớp động nối nó với các khâu khác.
Ví dụ 3:
Lược đồ động của khâu thanh truyền (2) trong động cơ đốt trong (hình 1.12).
li
Hình 1.12. Lược đồ khâu
1.1.5. Chuỗi động và cơ cấu
a. Chuỗi động
+ Chuỗi động là tập hợp các khâu được nối với nhau bằng các khớp động.
+ Dựa trên cấu trúc chuỗi động, ta phân chuỗi động thành hai loại: chuỗi động hở và chuỗi động kín.
Chuỗi động hở là chuỗi động trong đó các khâu chỉ được nối với một khâu khác. Chuỗi động kín là chuỗi động trong đó mỗi khâu được nối ít nhất với hai khâu khác (các khâu tạo thành các chu vi khép kín, mỗi khâu tham gia ít nhất hai khớp động).
+ Dựa trên tính chất chuyển động, ta phân biệt chuỗi động không gian và chuỗi động phẳng. Chuỗi động không gian có các khâu chuyển động trên các mặt phẳng không song song với nhau, còn trong chuỗi động phẳng, tất cả các khâu chuyển động trên những mặt phẳng song song với nhau.
+ Ví dụ 1:
Chuỗi động trên hình 1.13, có 4 khâu nối với nhau bằng 3 khớp quay và 1 khớp trượt, các khớp quay có đường trục song song với nhau và vuông góc với phương trượt của khớp trượt, do đó cả 4 khâu có mặt phẳng chuyển động song song với nhau. Hơn nữa mỗi khâu trong chuỗi động nối động với 2 khâu khác, nên chuỗi động nói trên là một chuỗi động phẳng kín.
Hình 1.13. Chuỗi động phẳng kín
Tương tự, chuỗi động trên hình 1.14 cũng là chuỗi động phẳng kín.
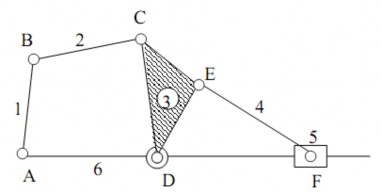
Hình 1.14. Chuỗi động phẳng kín
Chuỗi động trên hình 1.15 gồm 4 khâu, nối nhau bằng 3 khớp quay có đường trục vuông góc với nhau tường đôi một, do đó các khâu chuyển động trong các mặt phẳng không song song với nhau. Mặt khác, khâu 3 và khâu 4 chỉ được nối với một khâu khác nên đây là một chuỗi động không gian hở.
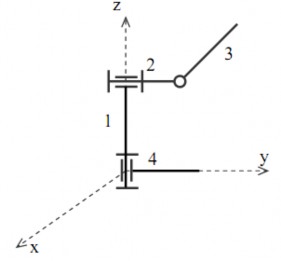
Hình 1.15. Chuỗi động không gian hở
b. Cơ cấu
+ Cơ cấu là một chuỗi động, trong đó một khâu được chọn làm hệ quy chiếu (còn gọi là giá), các khâu còn lại có chuyển động xác định trong hệ quy chiếu này (còn gọi là các khâu động). Thông thường, coi giá là cố định.
Tương tự như chuỗi động, ta cũng phân biệt cơ cấu phẳng và cơ cấu không gian.
Ví dụ:
Chọn khâu 4 trong chuỗi động phẳng kín (hình 1.13), khâu 6 trong chuỗi động phẳng kín (hình 1.14) làm giá, ta được các cơ cấu phẳng. Chọn khâu 4 trong chuỗi động không giản hở (hình 1.15) làm giá, ta có cơ cấu không gian.
4
Hình 1.16. Cơ cấu tay quay con trượt
Hình 1.16 cơ cấu tay quay con trượt dùng để biến chuyển động quay của khâu 1 thành chuyển động tịnh tiến của khâu 3 và ngược lại.
Hình 1.17 cơ cấu 6 khâu phẳng sử dụng trong máy sàng lắc, dùng để biến chuyển động quay của khâu 1 thành chuyển động tịnh tiến qua lại của con trượt 5. Hình 1.18 cơ cấu tay máy ba bậc tự do.
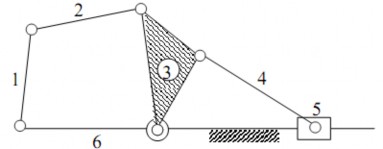
Hình 1.17. Cơ cấu 6 khâu phẳng
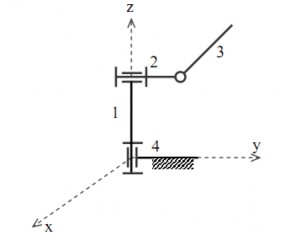
Hình 1.18. Cơ cấu tay máy
+ Cơ cấu thường được tạo thành từ chuỗi động kín. Cơ cấu được tạo thành từ chuỗi động hở như cơ cấu tay máy (hình 1.18), cơ cấu rô to máy điện (hình 1.19).
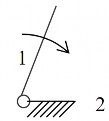
Hình 1.19. Cơ cấu rô to
1.2. Bậc tự do của cơ cấu phẳng
1.2.1 Khái niệm bậc tự do của cơ cấu
+ Số bậc tự do của cơ cấu là số thông số vị trí độc lập cần cho trước để vị trí của toàn bộ cơ cấu hoàn toàn xác định. Số bậc tự do của cơ cấu cũng chính bằng số quy luật chuyển động cần cho trước để chuyển động của cơ cấu hoàn toàn xác định.
Ví dụ:
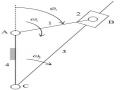
Xét cơ cấu bốn khâu bản lề ABCD (hình 1.20) gồm giá cố định 4 và ba khâu
động 1, 2, 3. Nếu cho trước thông số υ1= (𝐴𝐷, 𝐴𝐵) để xác định vị trí của khâu 1 so với giá thì vị trí của cơ cấu hoàn toàn xác định. Thật vậy, do kích thước động lAB đã
cho trước nên vị trí điểm B hoàn toàn xác định. Do điểm D và các kích thước lBC, lCD đã cho trước nên vị trí điểm C và do đó vị trí các khâu 2 và 3 hoàn toàn xác định. Nếu cho trước quy luật chuyển động của khâu (1): υ1 = υ1(t) thì chuyển động của các khâu 2 và 3 sẽ hoàn toàn xác định. Như vậy cơ cấu bốn khâu bản lề có 1 bậc tự do: W=1.
![]()
Hình 1.20. Cơ cấu 4 khâu bản lề
1.2.2. Công thức tính bậc tự do của cơ cấu
a. Xét cơ cấu gồm giá cố định và n khâu động.
Gọi W0 là tổng số bậc tự do của các khâu động của cơ cấu khi để rời nhau trong hệ quy chiếu gắn liền với giá. R là tổng số các ràng buộc do các khớp trong cơ cấu tạo ra. Khi đó bậc tự do của cơ cấu sẽ bằng : W = W0 – R
Do mỗi khâu động khi để rời sẽ có 6 bậc tự do nên tổng số bậc tự do của n khâu động là: W0 = 6n
Để tính bậc tự do của cơ cấu, cần tính R.
b. Đối với các cơ cấu mà lược đồ không có một đa giác nào cả, tức là không có khớp nào là khớp đóng kín (ví dụ cơ cấu tay máy hình 1.18), sau khi nối n khâu động lại với nhau và với giá pj khớp loại j, tổng số các ràng buộc bằng:
R = jp j
j
Do đó ta có
( mỗi khớp loại j hạn chế j bậc tự do tương đối, nghĩa là tạo ra j ràng buộc).
Ví dụ
W=6n -
jp j j
(1.1)
Với cơ cấu tay máy (hình 1.18): n= 3, p5 = 3 ( ba khớp quay loại 5) => W= 3.6 – (3.5) =3.
c. Đối với các cơ cấu mà lược đồ là một hay một số đa giác đóng kín, hoặc đối với một số cơ cấu có các đặc điểm về hình học, ta phải xét đến các ràng buộc trùng và ràng buộc thừa trong các công thức tính bậc tự do. Khi đó ta có:
W= 6n – ( jp j - Rtrùng - Rthừa) (1.2)
j