Khóa luận bao gồm:
Lời mở đầu: Trình bày sơ lược về thanh toán từ xa qua mạng công khai Chương 1: Các khái niệm cơ bản
Chương 2: Tổng quan về thanh toán từ xa Chương 3: Các giao thức thanh toán tiền điện tử
Chương 4: Chương trình mô phỏng hệ thống Digital Cash
Tuy nhiên, do còn nhiều hạn chế về thời gian cũng như khả năng của bản thân, khoá luận này không thể tránh khỏi thiếu sót. Em rất mong nhận được sự quan tâm và đóng góp ý kiến của các thầy, cô giáo cũng như các anh, chị và các bạn những người quan tâm đến lĩnh vực này.
Em xin chân thành cảm ơn!
Chương 1. CÁC KHÁI NIỆM CƠ BẢN
1.1 CÁC KHÁI NIỆM TRONG TOÁN HỌC
Có thể bạn quan tâm!
-
Nghiên cứu một số giao thức thanh toán qua mạng công khai - 1 -
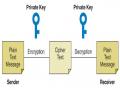
Mã Hoá Và Giải Mã Của Hệ Mã Hoá Khoá Công Khai -
Sơ Đồ Chữ Ký Mù Dựa Trên Chữ Ký Rsa -
Thanh Toán Trực Tuyến Và Thanh Toán Ngoại Tuyến
Xem toàn bộ 72 trang tài liệu này.
1.1.1 Số nguyên tố và nguyên tố cùng nhau
Số nguyên tố là số nguyên dương chỉ chia hết cho 1 và chính nó. Ví dụ 1,2,3… Các hệ mật mã thường dùng các số nguyên tố cỡ 512 bit hoặc lớn hơn
Hai số nguyên dương m và n được gọi là nguyên tố cùng nhau, nếu ước số chung lớn nhất của chúng bằng 1, ký hiệu gcd(m, n) = 1.
Ví dụ: 8 và 17 là hai số nguyên tố cùng nhau.
1.1.2 Hàm Euler
1) Định nghĩa
Cho n1, (n) được định nghĩa là số lượng các số nguyên trong khoảng từ [1, n) nguyên tố cùng nhau với n. Hàm được gọi là hàm Euler.
2) Tính chất
1/ Nếu p là số nguyên tố thì (p)=p-1.
2/ Hàm Euler là hàm có tính nhân:
Nếu gcd(m, n)=1 thì (m*n)=(m). (n).
3/ Nếu n=p1e1. p2e2... pkek một biểu diễn gồm các thừa số nguyên tố của, n thì:
(n)
1 1 1
1
n 1
p
p ...1 p
1 2 k
1.1.3 Đồng dư thức
1) Định nghĩa
Cho a và b là các số nguyên, khi đó a được gọi là đồng dư với b theo modulo n, ký hiệu là a b mod n nếu a, b chia cho n có cùng số dư. Số nguyên n được gọi là modulo của đồng dư.
Ví dụ: 5 7 mod 2 vì: 5 mod 2 = 1 và 7 mod 2 = 1
2) Tính chất
Cho a, a1, b, b1, cZ. Ta có các tính chất sau:
1/ a b mod n nếu và chỉ nếu a và b có cùng số dư khi chia cho n
2/ Tính phản xạ: a a mod n
3/ Tính đối xứng: Nếu a b mod n thì b a mod n
4/ Tính giao hoán: Nếu a b mod n và b c mod n thì a c mod n
5/ Nếu a a1 mod n, b b1 mod n thì a+b (a1+b1 )mod n và ab a1b1 mod n
3) Lớp tương đương
Lớp tương đương của một số nguyên a là tập hợp các số nguyên đồng dư với a
theo modulo n.
Cho n cố định đồng dư với n trong không gian Z vào các lớp tương đương. Nếu a=qn +r, trong đó 0 r n thì a r mod n. Vì vậy mỗi số nguyên a là đồng dư theo modulo n với duy nhất một số nguyên trong khoảng từ 0 đến n-1 và được gọi là thặng dư nhỏ nhất của a theo modulo n. Cũng vì vậy, a và r cùng thuộc một lớp tương đương. Do đó r có thể đơn giản được sử dụng để thể hiện lớp tương đương.
1.1.4 Không gian Zn và Zn*
Không gian các số nguyên theo modulo n:
Zn là tập hợp các số nguyên không âm nhỏ hơn n. Tức là: Zn = {0, 1, .., n-1}
Tất cả các phép toán trong Zn đều được thực hiện theo modulo n. Ví dụ: Z25 ={0, 1, 2,..., 24}. Trong Z25: 12 + 20 = 7(mod 25)
Không gian Zn* là tập hợp các số nguyên p thuộc Zn sao cho ước chung lớn nhất
của p và n là 1. Tức là, Zn* = {p thuộc Zn | gcd(n, p) = 1} Ví dụ: Z2 = { 0, 1 }; Z*2 =| 1 | vì gcd(1, 2)=1
1.1.5 Khái niệm phần tử nghịch đảo trong Zn
1) Định nghĩa
Cho aZn. Nghịch đảo nhân của a theo modulo n là một số nguyên xZn sao cho a*x1 (mod n). Nếu tồn tại thì đó là giá trị duy nhất và a gọi là khả nghịch, nghịch đảo của a ký hiệu là a-1.
2) Tính chất
1/ Cho a, bZn. Phép chia của a cho b theo modulo n là tích của a và b-1 theo modulo n, và chỉ được xác định khi b có nghịch đảo theo modulo n.
2/ Giả sử d=gcd(a, n). Phương trình đồng dư ax b (mod n) có nghiệm x nếu và chỉ nếu d chia hết cho b, trong trường hợp các nghiệm d nằm trong khoảng 0 đến n-1 thì các nghiệm đồng dư theo modulo n/d.
Ví dụ: 4-1 = 7(mod 9) vì 4*7 1(mod 9).
1.1.6 Khái niệm nhóm
1) Nhóm
Nhóm là bộ các phần tử (G, *) thỏa mãn các tính chất sau:
1/ Tính chất kết hợp: ( x * y ) * z = x * ( y * z )
2/ Tính chất tồn tại phần tử trung gian e G: e * x= x * e = x, x G
3/ Tính chất tồn tại phần tử nghịch đảo x’ G: x’ * x = x * x’ = e
2) Nhóm con
Nhóm con là bộ các phần tử ( S, * ) là nhóm thỏa mãn các tính chất sau:
1/ S G, phần tử trung gian e S
2/ x, y S => x * y S
3) Nhóm cylic
Nhóm Cyclic là nhóm mà mọi phần tử x của nó được sinh ra từ một phần tử đặc biệt g G. Phần tử này được gọi là phần tử nguyên thủy, tức là:
Với x G: n N mà gn = x.
Ví dụ: (Z+, *) là một nhóm cyclic có phần tử sinh là 1
1.1.7 Các phép tính cơ bản trong không gian modulo
Cho n là số nguyên dương. Như trước, các phần tử trong Zn được thể hiện bởi các số nguyên {0, 1, 2, …, n-1}. Nhận xét rằng: nếu a, bZn thì:
a b if a+b (a+b) mod n = a b n if a b n Vì vậy, phép cộng modulo (và phép trừ modulo) có thể được thực hiện mà không cần thực hiện các phép chia dài. Phép nhân modulo của a và b được thực hiện bằng phép nhân thông thường a với b như các số nguyên bình thường, sau đó lấy phần dư của kết quả sau khi chia cho n. Phép tính nghịch đảo trong Zn có thể được thực hiện nhờ sử dụng thuật toán Euclidean mở rộng như mô tả sau: Nếu b=0 thì đặt d:=a; x:=1; y:=0; return(d; x; y) ; Đặt x2:=1; x1:=0 ; y2:=0 ; y1:=1 ; Khi b>0 thực hiện: q:=[a/b]; r=a-qb; x:=x2-qx1; y:=y2-qy1 ; a:=b; b:=r; x2:=x1; x1:=x; y2:=y1; y1:=y ; d:=a ; x:=x2 ; y:=y2 ; return(d, x, y) ; 1.1.8 Hàm một phía và hàm một phía có cửa sập 1) Hàm một phía Một hàm một phía là hàm mà dễ dàng tính toán ra quan hệ một chiều, nhưng rất khó để tính ngược lại. Ví như biết x thì có thể dễ dàng tính ra f(x), nhưng nếu biết f(x) thì rất khó tính ra được x. Trong trường hợp này “khó” có nghĩa là để tính ra được kết quả thì phải mất rất nhiều thời gian để tính toán. Ví dụ: Tính y = f(x) = αx mod p là dễ nhưng tính ngược lại x = logα y là bài toán “khó” (bài toán logarit rời rạc) 2) Hàm một phía có cửa sập F(x) được gọi là hàm một phía có cửa sập nếu tính xuôi y = f(x) thì dễ nhưng tính ngược x = f-1(y) thì khó tuy nhiên nếu có “cửa sập” thì vấn đề tính ngược trở nên dễ dàng. Cửa sập ở đây là một điều kiện nào đó giúp chúng ta dễ dàng tính ngược. Ví dụ: y = f(x) =xb mod n tính xuôi thì dễ nhưng tính ngược x= ya mod n thì khó vì phải biết a với a * b 1 (mod( (n)) trong đó (n) = (p-1)(q-1)). Nhưng nếu biết cửa sập p, q thì việc tính n = p * q và tính a trở nên dễ dàng. 1.1.9 Độ phức tạp tính toán Lý thuyết thuật toán và các hàm tính được ra đời từ những năm 30 của thế kỉ 20 đã đặt nền móng cho việc nghiên cứu các vấn đề “tính được”, “giải được” trong toán học. Tuy nhiên từ cái “tính được” đến việc tính toán thực tế là một khoảng cách rất lớn. Có rất nhiều vấn đề được chứng minh là có thể “tính được” nhưng không tính được trong thực tế cho dù có sự hỗ trợ của máy tính. Vào những năm 1960, lý thuyết độ phức tạp tính toán được hình thành và phát triển một cách nhanh chóng, cung cấp nhiều hiểu biết sâu sắc về bản chất phức tạp của các thuật toán và các bài toán, từ những bài toán thuần túy lý thuyết đến những bài toán thường gặp trong thực tế. Độ phức tạp tính toán (về không gian hay thời gian) của một tiến trình tính toán là số ô nhớ được dùng hay số các phép toán sơ cấp được thực hiện trong tiến trình tính toán đó. Dữ liệu đầu vào đối với một thuật toán thường được biểu diễn qua các từ trong một bảng ký tự nào đó. Độ dài của một từ là số ký tự trong từ đó. Cho một thuật toán A trên bảng ký tự Z ( tức là có các đầu vào là các từ trong Z). Độ phức tạp tính toán của thuật toán A được hiểu như một hàm số fa(n) sao cho với mỗi số n thì fa(n) là số ô nhớ, hay số phép toán sơ cấp tối đa mà A cần để thực hiện tiến trình tính toán của mình trên các dữ liệu vào có độ dài nhỏ hơn hoặc bằng n. Ta nói: thuật toán A có độ phức tạp thời gian đa thức, nếu có một đa thức P(n) sao cho với mọi n đủ lớn ta có: fa(n) p(n), trong đó fa(n) là độ phức tạp tính toán theo thời gian của A. Bài toán P được gọi là “giải được” nếu tồn tại thuật toán để giải nó, tức là thuật toán làm việc có kết thúc trên mọi dữ liệu đầu vào của bài toán. Bài toán P được gọi là “giải được trong thời gian đa thức” nếu có thuật toán giải nó với độ phức tạp thời gian đa thức. Các thuật toán có độ phức tạp giống nhau được phân loại vào trong các lớp tương đương. Ví dụ tất cả các thuật toán có độ phức tạp là n3 được phân vào trong lớp n3 và ký hiệu bởi 0(n3).