Quy Hoạch Thực Nghiệm Theo Kế Hoạch Mạng Đơn Hình Sheffe

Cochran theo công thức:

s 2

n

G max

i

s2

(2.3)

i1

và so sánh với giá trị tra bảng Gp( f, n), nếu G < Gp( f, n) thì các phương sai là đồng nhất và phương sai tái sinh có thể được tính như sau:

s

n 2

2 i

sts

i1

n

(2.4)

Khi đó giả sử ta tìm mô hình thực nghiệm thụ động mô tả sự phụ thuộc của độ bền kéo vào thành phần của các cấu tử ở dạng:

1 2 3

y A.x1 .x2 .x3

(2.5)

Trong đó A là hằng số,

1 ,

2 , 3

là các hệ số cần tìm.

Phương trình trên đưa về dạng tuyến tính sẽ có dạng:



lg y  lg



A 1 lg x1 2 lg x2 3 lg x3

(2.6)

Đặt

lg y Z1; lg A 0; lg x1 u1; lg x2 u2; lg x3 u3

Ta có thể đưa về dạng tuyến tính và áp dụng phương pháp bình phương tối

thiểu có thể nhận được hệ phương trình chuẩn:

n n n n

0 n1 u1i 2 u2i 3 u3i

zi

i1

1i

2

n n

i1

n

i1

i1

n n

i1 n u	i1 n u u	i1 	n u 2	i1 i1 n n (2.7) u u u z
2i i1	1 1i i1	2i 2	2i i1	3 2i i1	3i 2i i i1
n n u u u		u u u 2 u z
3i i1	1 1i i1	3i 2	2i	3i 3	3i 3i i

Có thể bạn quan tâm!

• Hệ Blend Trên Cơ Sở Cao Su Nbr Với Cao Su Thiên Nhiên Epoxy Hóa (Enr)
• Hệ Blend Trên Cơ Sở Cao Su Nbr Với Cr Và Pvc
• Phương Pháp Xác Định Tính Chất, Cấu Trúc Vật Liệu Cao Su Blend
• Nghiên Cứu Chế Tạo Vật Liệu Cao Su Blend Trên Cơ Sở Cao Su Nitril Butadien Và Nhựa Polyvinyl Clorua
• Ảnh Hưởng Của Hàm Lượng Pvc Tới Hệ Số Già Hóa Của Vật Liệu Blend
• Nghiên Cứu Chế Tạo Vật Liệu Cao Su Blend 3 Cấu Tử Trên Cơ Sở Cao Su Nitril Butadien, Cao Su Cloropren Và Polyvinyl Clorua

Xem toàn bộ 172 trang tài liệu này.

0 u1i

0

0

1

u 2 

u1i

u2i

3

u1i

u3i

u1i zi

Giải hệ phương trình tuyến tính không thuần nhất ta có thể tìm được các

hệ số

0 , 1 ,

2 và 3 . Thay vào phương trình tuyến tính ta có thể tìm được mô

hình toán học mô tả kết quả thí nghiệm. Mô hình được xem là tương hợp khi các



giá trị hàm mục tiêu tính toán theo mô hình y gần với giá trị thực nghiệm y

nghĩa là giá trị



y y y

phải nhỏ.

2.2.3.2. Quy hoạch thực nghiệm theo kế hoạch mạng đơn hình Sheffe

Đối với hệ ba cấu tử (đa cấu tử), tính chất của hệ chỉ phụ thuộc vào tỷ lệ thành phần các cấu tử thì kế hoạch thường dùng là mạng đơn hình Sheffe. Khi đó, nồng độ (hàm lượng) các cấu tử khác nhau thỏa mãn quan hệ.

3

i

x  1

i1

(2.8)

Trong đó xi ≥ 0. Quy hoạch mạng đơn hình Sheffe tìm mối quan hệ giữa

tỷ lệ thành phần lên độ bền kéo (y), độ dãn dài (z) và độ cứng (v) tương ứng với mô hình toán học (mô hình thực nghiệm – thống kê) như sau:



y f1x1, x2 , x3;



z f 2

x1, x2

, x3

và



v f3

x1, x2

, x3 

(2.9)

Đối với hệ 3 cấu tử NBR/CR/PVC tương ứng ký hiệu là x1, x2, x3 thì mô hình bậc 4 tương ứng mạng lưới {3,4} trong đó 3 là số cấu tử, 4 là bậc của đa thức được mô tả trong hình và kế hoạch thực nghiệm của nó ở bảng dưới đây:

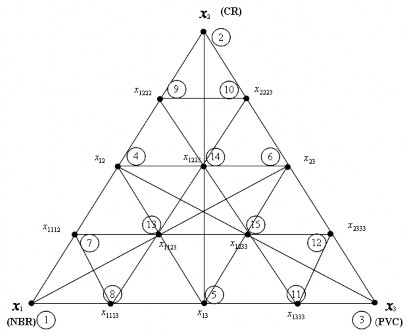
Hình 2.1. Mạng đơn hình Sheffe {3,4}

Bảng 2.5: Ma trận kế hoạch hóa của mạng {3,4}

STT

x1	x2	x3	y	z	v
1	1	0	0	y1	z1	v1
2	0	1	0	y2	z2	v2
3	0	0	1	y3	z3	v3
4	½	½	0	y12	z12	v12
5	½	0	½	y13	z13	v13
6	0	½	½	y23	z23	v23
7	¾	¼	0	y1112	z1112	v1112
8	¾	0	¼	y1113	z1113	v1113
9	¼	¾	0	y1222	z1222	v1222
10	0	¾	¼	y2223	z2223	v2223
11	¼	0	¾	y1333	z1333	v1333
12	0	¼	¾	y2333	z2333	v2333
13	½*	¼	¼	y1123	z1123	v1123
14	¼	½*	¼	y1223	z1223	v1223
15	¼	¼	½*	y1233	z1233	v1233

Mô hình toán với hệ là một đa thức bậc 4, cụ thể với độ bền kéo y có dạng: ŷ = 1x1 + 2x2 + 3x3 + 12x1x2 + 13x1x3 + 23x2x3 +

+ 12x1x2(x1-x2) + 13x1x3(x1-x3) + 23x2x3(x2-x3) + (2.10)

+ 12x1x2( x1-x2)2 + 13x1x3( x1-x3)2 + 23x2x3 (x2-x3)2 +

+ 1123x12x2x3 + 1223x1x22x3 + 1233x1x2x32

trong đó các hệ số được tính như sau:

1 = y1 ; 2 = y2 3 = y3

12 = 4y12 – 2y1 – 2y2 (2.11)

13 = 4y13 – 2y1 – 2y3

23 = 4y23 – 2y2 – 2y3

12 = - y1 + 2y1112 – 2y1222 + y2)

13 = - y1 + 2y1113 – 2y1333 + y3)

23 = - y2 + 2y2223 – 2y2333 + y3)

12 = - y1 + 4y1112 – 6y12 + 4y1222 – y2 )

13 = - y1 + 4y1113 – 6y13 + 4y1333 – y3 )

23 = - y2 + 4y2333 – 6y23 + 4y2333 – y3 )

1123 = 32 (3y1123 – y1223 – y1233) + 6y1 – y2 – y3) – 16(y12 + y13) –

– 5y1112 + 5y1113 – 3y1222 – 3y1333 – y2223 –y2333)

1223 = 32 (3y1223 – y1123 – y1233) + 6y2 – y1 – y3) – 16(y12 + y23) –

– 5y1222 + 5y2223 – 3y1112 – 3y2333 – y1113 –y1333)

1233 = 32 (3y1233 – y1123 – y1233) + 6y3 – y1 – y2) – 16(y13 + y23) –

– 5y1333 + 5y2333 – 3y1113 – 3y2223 – y1112 –y1222)

yn

Sau khi đã xác định các hệ số của phương trình hồi quy cần tiến hành phân tích thống kê các kết quả nhận được. Đó là kiểm tra tính tương hợp của phương trình. Do khi tiến hành thực nghiệm theo kế hoạch mạng đơn hình (là kế hoạch bão hòa) không còn bậc tự do để kiểm định tính tương hợp của phương trình. Bởi vậy cần phải tiến hành thêm những thí nghiệm bổ sung ở những điểm kiểm tra. Đối với mỗi điểm kiểm tra cần tìm đại lượng t theo công thức:

1 

t 

s y

(2.12)

Trong đó:

y 



y y

là giá trị tuyệt đối của hiệu số giữa giá trị thực nghiệm và

giá trị tính toán.

n – số thí nghiệm song song (lặp) ở từng điểm

y

s 2 - phương sai tái sinh

- đại lượng tìm từ giản đồ gồm các đường đẳng trị của . Giá trị chỉ phụ thuộc vào thành phần. Đối với hệ 3 cấu tử có thể tìm theo hình dưới:

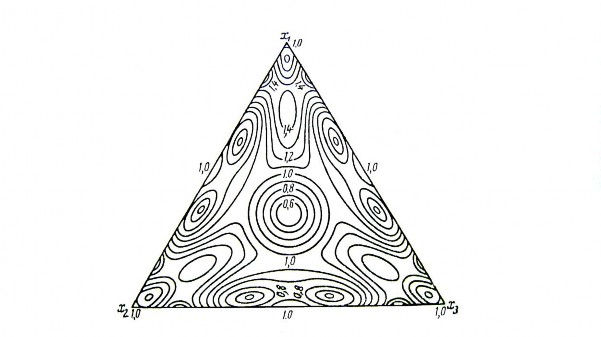
Hình 2.2. Đường đẳng trị của đối với mạng đơn hình {3,4}

Đại lượng t ở trên có phân bố Student và ta so sánh với giá trị tra bảng tp/2l(f); p – mức ý nghĩa, l – số điểm kiểm tra; f – số bậc tự do của phương sai tái

s

y

sinh 2 ở trên. Giả thiết về sự tương hợp của phương trình hồi quy với số liệu

thực nghiệm được thừa nhận nếu t < tp/2l(f) cho tất cả các điểm kiểm tra.

2.2.3.3. Quy hoạch thực nghiệm khảo sát phần cục bộ của biểu đồ thành phần – tính chất theo kế hoạch Mc Lean – Anderson

Trong quy hoạch thực nghiệm, khi nghiên cứu ảnh hưởng của thành phần lên tính chất đối với hệ đa cấu tử có thể xảy ra nhiều trường hợp mô hình không

tương hợp do có nhiều yếu tố tác động chưa được xác định. Vì vậy có thể thực hiện khảo sát vùng cục bộ của biểu đồ thành phần – tính chất theo kế hoạch Mc Lean – Anderson trên cơ sở giới hạn thông tin tích cực từ thực nghiệm. Bằng thực nghiệm đã chứng minh các cấu tử NBR, CR và PVC chỉ tương hợp với nhau ở những hàm lượng nhất định. Do đó để hệ có những tính chất tốt hơn thì hàm lượng 3 cấu tử NBR, CR, PVC tương ứng x1, x2, x3 thỏa mãn điều kiện:

a ≤ x1 ≤ b

c ≤ x2 ≤ d với a,b,c,d,e,f > 0 (2.13)

e ≤ x3 ≤ f

và x1+x2+x3 = 1 (2.14)

Trong nghiên cứu này, vùng cục bộ được mô tả cụ thể trong hình 3.20 phần Kết quả và thảo luận.

Kế hoạch Mc Lean – Anderson được xây dựng như sau:

1. Ta viết tất cả những tổ hợp khả dĩ của hai mức giới hạn trên dưới cho từng cặp hai cấu tử một (bỏ trống một cấu tử). Tổng số ta có: q.2m-1 = 3.23-1 = 12 tổ hợp. Trong đó: q là số cấu tử (3 cấu tử), m là số thí nghiệm lặp (3 lần).

Bảng 2.6. Tổ hợp thực nghiệm theo kế hoạch Mc Lean - Anderson

TT

x1	x2	x3	Điểm được chọn cho kế hoạch mới
1	a	-	e	x2 thỏa mãn điều kiện c ≤ x2 ≤ d
2	b	-	e
3	a	-	f
4	b	-	f
5	a	c	-	x3 thỏa mãn điều kiện e ≤ x3 ≤ f
6	b	c	-
7	a	d	-
8	b	d	-
9	-	c	e	x1 thỏa mãn điều kiện a≤ x1 ≤ b
10	-	c	f
11	-	d	e
12	-	d	f

2. Trong số 12 tổ hợp kể trên ta chọn tổ hợp để khi thêm thành phần thứ 3 thì thỏa mãn các điều kiện là tổng nồng độ các cấu tử phải bằng 1 và từng nồng độ nằm trong vùng giới hạn. Dễ dàng nhận thấy đó là các tổ hợp theo thứ tự: 2, 3, 6, 7, 10 và 11. Các điểm thực nghiệm của kế hoạch mới ký hiệu (1), (2), (3), (4), (5), (6) trong bảng trên (hình vẽ cụ thể được nêu trong phần Kết quả và thảo luận).

3. Ta chọn 6 điểm thí nghiệm mới trên các cạnh:

Số (7) của cạnh (1) – (3)

Số (8) của cạnh (1) – (6)

Số (9) của cạnh (2) – (4)

Số (10) của cạnh (2) – (5)

Số (11) của cạnh (3) – (5)

Số (12) của cạnh (4) – (6)

còn điểm (13) là tâm của lục giác. Tọa độ của 6 điểm bổ sung này là trung bình tọa độ của từng cặp, còn của tâm là trung bình tọa độ của 6 điểm mới.

Từ đó lập được bảng kế hoạch Kế hoạch Mc Lean – Anderson gồm 13 thí nghiệm (được mô tả chi tiết trong phần Kết quả và thảo luận). Từ đó tìm mô hình thực nghiệm thống kê của kế hoạch trên ở dạng đa thức rút gọn bậc 3 khuyết (chẳng hạn tìm mô hình cho độ bền kéo) được biểu diễn theo phương trình dưới

đây:



y 1x1 2 x2 3x3 12x1x2 13x1x3 23x2 x3 123x1x2 x3

(2.15)

Phương trình tuyến tính trên có 7 hệ số được xác định theo phương pháp bình phương tối thiểu với việc giải hệ phương trình chuẩn:

	13 x	2 		13 	x	x  ........	13 x2 x x	13 
1	i1	1i	2	i1	1i	2i	123 1 2 i1	3 i1
	13 x	x			13 	x2  ........	n x x2	13 x 
1 ...	i1 ...	1i 2 ...	i ...	2	i1	2i	123 1i 2i i1	3i i1
...	...	...	...
...	...	...	...
...	...	...	...
	13 x	2 x	x			13 x x2 x 	13 ........x2x2	13 x2 
1	i1	1i 2	i 3i		2	1i 2i 3i i1	123 1i 2i i1	3i i1

x1i

.yi

x2i

.yi

(2.16)

x1i

x2i

x3i yi

Thay các hệ số vừa tìm được vào mô hình trên và tính toán



yi và cả

y 



y y

để so sánh giữa giá trị hàm mục tiêu tính toán theo mô hình và thực

nghiệm. Để kiểm định tính tương hợp của mô hình có thể tiến hành bình thường. Cụ thể tính phương sai tương hợp theo công thức:

n 2

yiyi

s

2 i1 

th n l

(2.17)

Trong đó: n là số thí nghiệm theo kế hoạch Mc Lean – Anderson;

l: là số hệ số có nghĩa của phương trình tuyến tính (mô hình).

Sau đó tính chuẩn số Fisher theo công thức:

s2

s

2

F th

ts

(2.18)

Và so sánh giữa giá trị tính toán và giá trị tra bảng: nếu F < Fp(f1, f2) thì mô hình phù hợp với kết quả thực nghiệm (mô hình tương hợp) và có thể sử dụng cho mục đích tiếp theo là tìm giá trị tối ưu cho độ bền kéo. Bằng phương pháp tính toán tương tự có thể tìm được mô hình tương hợp cho độ dãn dài và độ cứng của hệ vật liệu cao su blend ba cấu tử NBR/CR/PVC.

Xem tất cả 172 trang.