Thiết Kế Phân Mảnh Ngang Dẫn Xuất

Ví dụ 3.15: Xét hệ thống quản lý dự án trong ví dụ 3.2. m1: (VT=„Nam Định„) (VT=„Hà Nội„) m2: (VT=„Nam Định„) (VT=„Hà Nội„) m3: (VT=„Nam Định„) (VT=„Hà Nội„)

m4: (VT=„Nam Định„) (VT=„Hà Nội„) M={m1, m2, m3, m4}

Khi đó, các vị từ m1, m4 mâu thuẫn với tập hợp các phép suy diễn I. Do đó có thể loại bỏ chúng ra khỏi tập hợp M. Trong tập hợp I, các vị từ m2 và m3 có thể rút gọn:

m2: VT=„Nam Định„ m3: VT=„Hà Nội„

Cuối cùng, M={m2, m3}

Ví dụ 3.16: Xét hệ thống quản lý dự án trong ví dụ 3.2. m1: (LUONG<3000) (LUONG≥3000)

m2: (LUONG<3000) (LUONG≥3000)

m3: (LUONG<3000) (LUONG≥3000) m4: (LUONG<3000) (LUONG≥3000)

M={m1, m2, m3, m4}

Khi đó, các vị từ m1, m4 mâu thuẫn với tập hợp các phép suy diễn I. Do đó có thể loại bỏ chúng ra khỏi tập hợp M. Trong tập hợp I, các vị từ m2 và m3 có thể rút gọn:

m2: LUONG<3000 m3: LUONG≥3000

Cuối cùng, M={m2, m3}

Ví dụ 3.17: Xét hệ thống quản lý dự án trong ví dụ 3.2. Giả sử có một ứng dụng truy xuất DA theo vị trí thực hiện dự án, áp dụng thuật toán COM_MIN và PHORIZONTAL để:

- Phân mảnh ngang chính quan hệ DA

- Phân mảnh ngang dẫn xuất quan hệ HS

Các bước thiết kế phân mảnh ngang chính quan hệ toàn cục DA:

Bước 1: Lược đồ toàn cục (Theo đề bài)

Bước 2: Vẽ đồ thị kết nối biểu diễn mối liên hệ giữa các quan hệ toàn cục (Trong ví dụ 3.2)

Bước 3: Tìm tập các vị từ đơn giản PDA PDA={p1, p2}

+ p1: VT=„Nam Định„

+ p2: VT=„Hà Nội„

Bước 4: Tìm tập các vị từ đầy đủ và tối thiểu PDA„ =COM_MIN(PDA, DA):

F=

1

Xét p1 chia DA theo quy tắc 1 thành 2 phần f1= σp

1

(DA) và f2= σp (DA);

PDA„={p1} PDA={p2} F={f1, f2}

Xét p2 không chia mảnh nào của F

PDA„={p1} PDA={p2} F={f1, f2}

Vậy PDA„={p1} là tối thiểu và đầy đủ

Chú ý: Nếu xét p2 trước thì PDA„={ p2} là tối thiểu và đầy đủ.

Bước 5: Tìm tập hợp các vị từ giao tối thiểu định nghĩa trên PDA‟: M={m1, m2} m1=p1, m2=p1

Bước 6: Tìm tập các phép suy diễn I=

Bước 7: Tìm tập các vị từ giao tối thiểu có nghĩa M‟= PHORIZONTAL(PDA, DA)={m1, m2}

+ PDA„ =COM_MIN(PDA, DA):

+ M={m1, m2}

+ I=

Nên M‟= {m1, m2}

Bước 8: Viết biểu thức phân mảnh ngang chính theo M‟

DA1= σm (DA) = σp

(DA)= σ VT=„Nam Định„ (DA)

1

2

DA2= σm

1

1

(DA)= σp (DA)= σ (VT=„Nam Định„) (DA)

Kết quả phân mảnh:

DA1

MADA

TENDA	NS	VT
D1	CSDL	20000	Nam Định
D4	PHÁT TRIỂN	25000	Nam Định

Có thể bạn quan tâm!

• Vấn Đề Thiết Kế Cơ Sở Dữ Liệu Phân Tán
• Thiết Kế Phân Mảnh Cơ Sở Dữ Liệu
• Cơ sơ dữ liệu phân tán - 17
• Kiểm Tra Điều Kiện Đúng Đắn Khi Phân Mảnh Ngang
• Cơ sơ dữ liệu phân tán - 20
• Kiểm Tra Tính Đúng Đắn Khi Phân Mảnh Dọc

Xem toàn bộ 312 trang tài liệu này.

DA2

MADA

TENDA	NS	VT
D2	CÀI ĐẶT	12000	Hà Nội
D3	BẢO TRÌ	28000	Hà Nội

Ví dụ 3.18: Xét hệ thống quản lý dự án trong ví dụ 3.2. Giả sử hệ thống có các ứng dụng sau:

Ứng dụng 1: Truy xuất các bộ của DA theo vị trí là “Nam Định”

Ứng dụng 2: Truy xuất các bộ của DA có ngân sách bằng 25000 Ứng dụng 3: Truy xuất các bộ của DA có ngân sách khác 25000 Áp dụng thuật toán COM_MIN và PHORIZONTAL để:

- Phân mảnh ngang chính quan hệ DA

- Phân mảnh ngang dẫn xuất quan hệ HS

Các bước thiết kế phân mảnh ngang chính quan hệ toàn cục DA:

Bước 1: Lược đồ toàn cục (Theo đề bài)

Bước 2: Vẽ đồ thị kết nối biểu diễn mối liên hệ giữa các quan hệ toàn cục (Trong ví dụ 3.2)

Bước 3: Tìm tập các vị từ đơn giản PDA PDA={p1, p2, p3}

+ p1: VT=„Nam Định„

+ p2: NS= 25000

+ p3: NS ≠ 25000

Bước 4: Tìm tập các vị từ đầy đủ và tối thiểu PDA„ =COM_MIN(PDA, DA):

F=

1

1

Xét p1 chia DA theo quy tắc 1 thành 2 phần f1= σp (DA) và f2= σp (DA);

PDA„={p1} PDA={p2, p3} F={f1, f2}

2 2

Xét p2 chia f1 theo quy tắc 1 thành 2 phần f11= σp (f1) và f12= σp (f1); PDA„={p1, p2}

PDA={p3}

F={f11, f12, f2}

p1 là vị từ thích hợp vì:

+ Tồn tại m1 và m3 chỉ khác nhau ở p1 (m1=p1  p2 ,m3=p1  p2)

1

+ Ứng dụng 1, 2 truy xuất đến mảnh DA1= σm (DA); ứng dụng 2 truy

3

xuất đến mảnh DA3== σm

(DA);

p2 là vị từ thích hợp vì:

+ Tồn tại m1 và m2 chỉ khác nhau ở p2 (m1=p1  p2 , m2=p1 p2)

1

+ Ứng dụng 1, 2 truy xuất đến mảnh DA1= σm (DA); ứng dụng 1, 3 truy

xuất đến mảnh DA2= σm2(DA);

Xét p3chia f3theo quy tắc 1 thành 2 phần f21= σp3(f2) và f22= σp3(f2); PDA„={p1, p2, p3}

PDA= 

F={f11, f12, f21, f22}

Khi đó ta có tập vị từ giao tối thiểu M={m1, m2, m3, m4, m5, m6, m7, m8}

Sử dụng tính chất phủ định của đẳng thức Attribute=Value là Attribute  Value p3 p2 ta có

m1=p1  p2  p3 = False

m2=p1  p2 p3 = p1  p2 m3=p1 p2  p3 = p1 p2 m4=p1 p2 p3 =False m5=p1  p2  p3 = False m6=p1  p2 p3 = p1  p2 m7=p1 p2  p3 = p1 p2 m8=p1 p2 p3 = False

p1 là vị từ thích hợp vì:

+ Tồn tại m1 và m3 chỉ khác nhau ở p1 (m2=p1  p2 ,m6=p1  p2)

2

+ Ứng dụng 1, 2 truy xuất đến mảnh DA2= σm (DA); ứng dụng 2 truy

6

xuất đến mảnh DA6= σm

(DA);

p2 là vị từ thích hợp vì:

+ Tồn tại m1 và m2 chỉ khác nhau ở p2 (m2=p1  p2 , m3=p1 p2)

2

+ Ứng dụng 1, 2 truy xuất đến mảnh DA2= σm (DA); ứng dụng 1, 3 truy

3

xuất đến mảnh DA3= σm

(DA);

p3 là không là vị từ thích hợp vì không tồn tại mi chứa p3 và mj chứa p3 Vậy PDA„={p1, p2} là tối thiểu và đầy đủ

Chú ý: Nếu sử dụng phép biến đổi tương tương p2 p3 ta có PDA„={p1, p3} là tối thiểu và đầy đủ.

Bước 5: Tìm tập hợp các vị từ giao tối thiểu định nghĩa trên PDA‟: M={m1, m2, m3, m4}

m1=p1  p2 m2=p1 p2 m3=p1  p2 m4=p1 p2 Bước 6: Tìm tập các phép suy diễn I=

Bước 7: Tìm tập các vị từ giao tối thiểu có nghĩa

M‟= PHORIZONTAL(PDA, DA)={m1, m2, m3, m4}

+ PDA„ =COM_MIN(PDA, DA):

+ M={m1, m2, m3, m4}

+ I=

Nên M‟= {m1, m2, m3, m4}

Bước 8: Viết biểu thức phân mảnh ngang chính theo M‟

DA1= σm (DA) = σp p

(DA)= σ VT=„Nam Định„ NS= 25000 (DA)

1 1 2

2

1

2

DA2= σm (DA)= σp p

(DA)= σ VT=„Nam Định„(NS= 25000) (DA)

3

DA3= σm

(DA)= σp  p

(DA)= σ (VT=„Nam Định„)  NS= 25000 (DA)

1

2

4

DA4= σm

(DA)= σp p

(DA)= σ (VT=„Nam Định„)(NS= 25000) (DA)

1 2

Kết quả phân mảnh:

DA1

MADA

TENDA	NS	VT
D4	PHÁT TRIỂN	25000	Nam Định

DA2

MADA

TENDA	NS	VT
D1	CSDL	20000	Nam Định

DA3=

MADA

TENDA	NS	VT

DA4

MADA

TENDA	NS	VT
D2	CÀI ĐẶT	12000	Hà Nội
D3	BẢO TRÌ	28000	Hà Nội

3.3.3. Thiết kế phân mảnh ngang dẫn xuất

1) Định nghĩa thiết kế phân mảnh ngang dẫn xuất

Phân mảnh ngang dẫn xuất của một quan hệ toàn cục R không dựa trên các đặc tính của các thuộc tính riêng của nó, mà được suy dẫn từ mảnh ngang của một quan hệ khác.

Phân mảnh ngang dẫn xuất được định nghĩa trên trên các quan hệ bộ phận của đường liên hệ theo phép chọn trên quan hệ chủ của đường liên hệ này. Điều quan trọng cần nhớ hai điểm:

Thứ nhất, đường liên hệ giữa quan hệ chủ và quan hệ bộ phận được định nghĩa là một phép kết nối bằng.

Thứ hai, một phép kết nối bằng có thể thực hiện bằng các phép nửa kết nối.

Điểm thứ hai là đặc biệt quan trọng đối với các mục đích của chúng ta, bởi vì chúng ta muốn phân chia quan hệ bộ phận theo sự phân mảnh của quan hệ chủ của nó,

nhưng chúng ta cũng muốn mảnh kết quả chỉ được định nghĩa trên các thuộc tính của quan hệ bộ phận.

Cho trước một đường liên hệ L với owner(L) = S và member(L) = R, các mảnh ngang dẫn xuất của R được định nghĩa như sau:

Ri =R F Si , 1 i n

Trong đó:

- n là số lượng lớn nhất các mảnh sẽ được định nghĩa trên R

i

- Si = F (S)

- Fi là công thức dùng để định nghĩa mảnh ngang chính Si

- F là điều kiện nửa kết nối (semi - join condition).

Quan hệ R có thể là quan hệ chủ của một đường liên hệ khác L‟ và quan hệ bộ phận là T, và cứ như thế. Trong trường hợp tổng quát, chúng ta có thể có một cây phân mảnh ngang dẫn xuất (derived horizontal fragmentation tree), trong đó nút cha là quan hệ chủ và các nút con của nó là các quan hệ bộ phận.

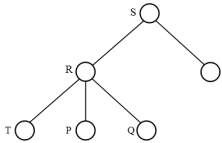
Để thực hiện phân mảnh ngang dẫn xuất, có ba dữ liệu vào là:

- Tập hợp các mảnh con của quan hệ chủ

- Quan hệ bộ phận

- Tập hợp các vị từ nửa kết nối giữa quan hệ chủ và quan hệ bộ phận

2) Các bước thiết kế phân mảnh ngang dẫn xuất theo chiến lược từ trên xuống. Bước 1: Tìm lược đồ toàn cục

Bước 2: Vẽ đồ thị kết nối biểu diễn mối liên hệ giữa các quan hệ toàn cục Bước 3: Tìm tập các vị từ đơn giản PS

Bước 4: Tìm tập các vị từ đầy đủ và tối thiểu

PS‟=COM_MIN(PS,S)={p1, p2,…, pn}

Bước 5: Tìm tập hợp các vị từ giao tối thiểu M= {m1, m2,…, mk} có thể được định nghĩa trên PS‟

Bước 6: Tìm tập các phép suy diễn I={i1, i2, …, ih} Bước 7: Tìm tập các vị từ giao tối thiểu có nghĩa

M‟= PHORIZONTAL(PS, S)={m1, m2,…, mg}

Bước 8: Viết biểu thức phân mảnh ngang chính theo M‟

i

Si = σm (S); 1 i g

Bước 9: Viết biểu thức phân mảnh dẫn xuất Ri =R F Si , 1 i g

Ví dụ 3.19: Xét ví dụ 3.17

Các bước thiết kế phân mảnh ngang dẫn xuất quan hệ toàn cục HS:

Từ bước 1 đến bước 8 đã được thực hiện trong ví dụ 3.17 Bước 9: Các biểu thức phân mảnh ngang dẫn xuất

HS1= HS 

HS2= HS 

HS.MaDA= DA.MaDADA1 HS.MaDA= DA.MaDADA2

Kết quả phân mảnh ngang dẫn xuất:

HS1

MANV

MADA	NV	TG
A1	D1	Quản lý	12
A2	D1	Phân tích	34
A3	D4	Lập trình	10
A6	D4	Kỹ thuật	36

HS2

MANV

MADA	NV	TG
A2	D2	Phân tích	6
A3	D3	Kỹ thuật	12
A4	D2	Quản lý	6
A5	D2	Quản lý	20
A7	D3	Quản lý	48
A8	D3	Lập trình	15

Ví dụ 3.20: Xét ví dụ 3.18

Các bước thiết kế phân mảnh ngang dẫn xuất quan hệ toàn cục HS:

Từ bước 1 đến bước 8 đã được thực hiện trong ví dụ 3.18 Bước 9: Các biểu thức phân mảnh ngang dẫn xuất

HS1= HS 

HS2= HS HS3= HS HS4= HS 

HS.MaDA= DA.MaDADA1 HS.MaDA= DA.MaDADA2 HS.MaDA= DA.MaDADA3 HS.MaDA= DA.MaDADA4

Kết quả phân mảnh ngang dẫn xuất:

HS1

MANV

MADA	NV	TG
A3	D4	Lập trình	10
A6	D4	Kỹ thuật	36

HS2

MANV

MADA	NV	TG
A1	D1	Quản lý	12
A2	D1	Phân tích	34

HS3=

MANV

MADA	NV	TG

HS

MANV

MADA	NV	TG
A2	D2	Phân tích	6
A3	D3	Kỹ thuật	12
A4	D2	Quản lý	6
A5	D2	Quản lý	20
A7	D3	Quản lý	48
A8	D3	Lập trình	15

3) Đồ thị kết nối

Phân mảnh ngang dẫn xuất được dùng để tạo điều kiện thuận lợi cho phép kết nối giữa các mảnh.

Một phép kết nối phân tán (distributed join) là một phép kết nối giữa các quan hệ được phân mảnh ngang. Khi một ứng dụng cần thực hiện phép kết nối giữa hai quan hệ toàn cục R và S, thì tất cả các bộ của R và của S phải được so sánh với nhau.

Do đó theo nguyên tắc, cần phải so sánh tất cả các mảnh Ri của R với tất cả các mảnh Sj của S:

R F S = (i Ri) F (j Sj)

Tuy nhiên, đôi khi có thể suy diễn để xác định một số phép liên hệ từng phần Ri Sj là rỗng:

R F S = (ij(Ri F Sj)

Đối với sự phân tán dữ liệu cho trước, điều này xảy ra khi các giá trị của thuộc tính kết nối của Ri và Sj là khác nhau.

Một phép kết nối phân tán được biểu diễn một cách hiệu quả bằng đồ thị kết nối

(join graph).