Cơ sơ dữ liệu phân tán - 20

+ aff(A1, A2) = 0

+ Vì (use(q1,A1) = 1  use(q1,A3) = 1)=true nên k=1

1

aff (A1, A3 ) 

k1

3



Có thể bạn quan tâm!

• Cơ sơ dữ liệu phân tán - 17
• Thiết Kế Phân Mảnh Ngang Dẫn Xuất
• Kiểm Tra Điều Kiện Đúng Đắn Khi Phân Mảnh Ngang
• Kiểm Tra Tính Đúng Đắn Khi Phân Mảnh Dọc
• Cơ sơ dữ liệu phân tán - 22
• Các Phép Biến Đổi Tương Đương Dùng Cho Các Truy Vấn

Xem toàn bộ 312 trang tài liệu này.

m1

accm (qk )  acc1 (q1 )  acc2 (q1 )  acc3 (q1 )

= 15 + 20 + 10 = 45

+ Vì (use(q4,A1) = 1  use(q4,A4) = 1)=true nên k=4

4

aff (A1 , A4 ) 

k 4

3



m1

accm (qk )  acc1 (q4 )  acc2 (q4 )  acc3 (q4 )

= 3 + 0 + 0 = 3

+ Vì (use(q2,A2) = 1  use(q2,A2) = 1)=true (use(q3,A2) = 1  use(q3,A2) = 1)=true nên k=2, k=3

3 3

aff(A2, A2) =

accm(q2) accm(q3)

m1 m1

= acc1(q2) + acc2(q2) + acc3(q2) + acc1(q3) + acc2(q3) + acc3(q3)

= 5 + 0 + 0 + 25 + 25 +25= 80

+ Vì (use(q2,A2) = 1  use(q2,A3) = 1)=true nên k=2

2

aff (A2 , A3 ) 

k2

3



m1

accm (qk )  acc1 (q2 )  acc2 (q2 )  acc3 (q2 )

= 5 + 0 + 0=5

+ Vì (use(q3,A2) = 1  use(q3,A4) = 1)=true nên k=3

3

aff (A2 , A4 ) 

k3

3



m1

accm (qk )  acc1 (q3 )  acc2 (q3 )  acc3 (q3 )

= 25 + 25 + 25=75

+ Vì (use(q1,A3) = 1  use(q1,A3) = 1)=true (use(q2,A3) = 1  use(q2,A3) = 1)=true nên k=1, k=2

3 3

aff(A3, A3) =

accm(q1) accm(q2)

m1 m1

= acc1(q1) + acc2(q1) + acc3(q1) + acc1(q2) + acc2(q2) + acc3(q2)

= 15 + 20 + 10 + 5 +0 +0 = 50

+ aff(A3, A4) = 0

+ Vì (use(q3,A4) = 1  use(q3,A4) = 1)=true (use(q4,A4) = 1  use(q4,A4) = 1)=true nên k=3, k=4

3 3

aff(A4, A4) =

accm(q3) accm(q4)

m1 m1

= acc1(q3) + acc2(q3) + acc3(q3) + acc1(q4) + acc2(q4) + acc3(q4)

= 25 + 25 +25 + 3 + 0 + 0 = 78

Ta có ma trận ái lực AA:

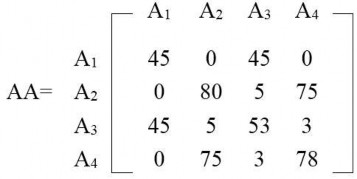
Ma trận ái lực thuộc sẽ được sử dụng trong phần còn lại của chương này để dựa vào đó phân mảnh dữ liệu. Quá trình này trước tiên gom các thuộc tính có ái lực lớn chung với nhau và dựa vào đó để phân chia quan hệ.

3.4.3. Giải thuật gom tụ

1) Ý tưởng giải thuật

Công việc cơ bản trong thiết kế giải thuật phân mảnh dọc là tìm kiếm một số cách gom nhóm thuộc tính của quan hệ dựa trên các giá trị thuộc tính trong AA.

Dùng giải thuật năng lượng liên hệ (BEA-Bond Energy Algorithm) để gom nhóm các thuộc tính của quan hệ.

Giải thuật BEA có những ưu điểm sau đây:

- Gom các thuộc tính có giá trị ái lực lớn chung với nhau.

- Gom nhóm các thuộc tính có giá trị ái lực nhỏ chung với nhau.

- Các nhóm cuối cùng không bị ảnh hưởng bởi thứ tự của các mục được dựa vào trong giải thuật.

- Thời gian tính toán của các giải thuật là O(n2) với n là số thuộc tính.

- Có thể nhận biết các mối liên hệ phụ giữa các nhóm thuộc tính gom phụ.

Ý tưởng:

- Hoán vị các hàng và các cột của ma trận ái lực thuộc tính AA thành ma trận ái lực gom tụ (CA- Clustered Affinity matrix) sao cho số đo ái lực chung (AM – global Affinity Measure) sau đây là lớn nhất:

n

AM 

i1

n



j1

aff (Ai , A j )[aff (Ai , A j1 )  aff (Ai , A j1 )  aff (Ai1, A j )  aff (Ai1, A j )]

với aff (Ao , A j )  aff (Ai , Ao )  aff (An1, A j )  aff (Ai , A jn1 )  0

- Hàm cực đại hoá chỉ xét các phần tử gần nhất nên chỉ gom các giá trị lớn với các giá trị lớn, các giá trị nhỏ nhất với giá trị nhỏ nhất. Do đó, ma trận ái lực thuộc tính (AA) là đối xứng nên:

n

AM 

i 1

n



j 1

aff ( Ai , Aj )[aff ( Ai , Aj 1) aff ( Ai , Aj 1)]

n



i1

n



j1

[aff (Ai , A j )aff (Ai , A j1 )  aff (Ai , A j )aff (Ai , A j1 )]

n



j1

n



i1

aff (Ai , A

j )aff (Ai , A

j1

n

) 

i1

[aff (Ai , A

j )aff (Ai , A



j1 )

Cầu nối (Bond) giữa hai thuộc tính Ax và Ay

n

bond(Ax , Ay ) 

z1

aff (Az , Ax )aff (Az , Ay )

n

AM 

j1

[bond(A j , A j1 )  bond(A j , A j1 )]

Xét n thuộc tính sau đây:

A1A2...Ai1 AiAjAi1...An

AM ' AM ''

Số đo ái lực chung cho các thuộc tính:

AMold = AM‟+AM”+bond(Ai-1,Ai)+bond(Ai, Aj)+bond(Aj, Ai)+bond(Aj, Aj+1)

n



l1

n

[bond(Al , Al1 )  bond(Ai , Al1 )]



li1

[bond(Al , Al1 )  bond(Ai , Al1 )]  2bond(Ai , A j )

có:

Xét việc đặt thuộc tính mới Ak giữa thuộc tính Ai, Aj trong ma trận ái lực gom tụ, ta

AMnew = AM‟ + AM” + bond(Ai, Ak) + bond(Ak, Ai) + bond(Ak, Aj) + bond(Aj,

Ak) = AM‟ + AM” + 2bond(Ai, Ak)+ 2bond(Ak, Aj)

Đóng góp thực cho số đo ái lực chung khi đặt thuộc tính Ak giữa Ai và Aj là: Cont(Ai, Ak, Ai) = AMnew – AMold =2 bond(Ai, Ak) + 2 bond(Ak, Aj) - 2 bond(Ai,Aj) Ví dụ 3.25: Xét ma trận AA được cho trong hình 3.5

- Đóng góp thực cho số đo ái lực chung khi đặt thuộc tính A4 vào giữa A1 và A2 cont(A1,A4,A2) = 2bond(A1,A4) + 2bond(A4,A2) - 2bond(A1,A2)

- Tính mỗi số hạng ta được:

bond(A1,A4) =

4



z1

aff (Az , A1 )aff (Az , A4 ) = aff(A1,A1)aff(A1,A4)+

aff(A2,A1)aff(A2,A4) +aff(A3,A1)aff(A3,A4)+aff(A4,A1)aff(A4,A4)

=483 + 075 + 450 + 378 = 378

4

bond(A4,A2) =



z1

aff (Az , A4 )aff (Az , A2 ) = aff(A1,A4)aff(A1,A2)+

aff(A2,A4)aff(A2,A2)+aff(A3,A4)aff(A3,A2)+aff(A4,A4)aff(A4,A2)

=30 + 7580 + 05 + 7872 = 11616

4

bond(A1,A2) =



z1

aff (Az , A1 )aff (Az , A2 ) = aff(A1,A1)aff(A1,A2)+

aff(A2,A1)aff(A2,A2)+aff(A3,A1)aff(A3,A2)+aff(A4,A1)aff(A4,A2)

=480 + 080 + 455 + 375 = 450

- Do đó cont(A1,A4,A2) = 2375 + 211616 - 2450 = 23988

Các bước chính của thuật toán

Bước 1: Khởi gán

Đặt và cố định cột 1 cột của AA vào trong CA. Bước 2: Thực hiện lặp

- Chọn mỗi cột trong n – i cột còn lại (i là số cột đã được đặt trong CA).

- Thử đặt chúng trong i + 1 vị trí còn lại trong ma trận CA.

- Chọn sắp đặt nào làm cho số đo ái lực chung có giá trị lớn nhất. Bước 3: Sắp thứ tự hàng

Mỗi lần xác định thứ tự cột, sắp đặt lại các hàng sao cho các vị trí tương đối của chúng khớp với các vị trí tương đối của các cột.

2) Giải thuật

Giải thuật 4.3 BEA

Đầu vào: AA: ma trận ái lực thuộc tính, n là số thuộc tính Đầu ra: CA: ma trận ái lực gom tụ

Begin

{Bắt đầu: nên nhớ rằng AA là một ma trận n*n} CA(•, 1)= AA(•, 1);

CA(•, 2)= AA(•, 2);

index = 3;

while index n do {chọn vị trí “tốt nhất” cho thuộc tính AAindex}

begin

for i=1 to index – 1 do

Tính cont(Ai-1, Aindex, Ai);

endfor

Tính cont(Aindex-1, Aindex, Aindex+1);{điều kiện biên} loc = nơi đặt, được cho bởi giá trị cont lớn nhất; for j= index downto loc do {di chuyển hai ma trận}

CA(•, j)= CA(•, j - 1);

endwhile

endfor

CA(•, loc)= AA(•, index); index = index + 1;

Sắp thứ tự các hàng theo thứ tự tương đối của các cột

End. {BEA}

Nhận xét:

- Cách tính toán cont tại các điểm cực trái (A1)

+ Giả sử thuộc tính Ak được đặt vào bên trái của thuộc tính cực trái A1

+ Vì không có phần tử ở bên trái Ak nên ta thêm thuộc tính A0 vào bên trái Ak để tính được số đo ái lực chung.

Cont(A0,Ak,A1 )=2Bond(A0,Ak)+2Bond(Ak,A1)-2Bond(A0,A1)=2Bond(Ak, A1)

vì Bond(A0,Ak)=Bond(A0,A1)=0

- Cách tính toán cont tại các điểm cực phải (An)

+ Giả sử thuộc tính Ak được đặt vào bên phải của thuộc tính cực phải An

+ Vì không có phần tử ở bên phải Ak nên ta thêm thuộc tính An+1 vào bên phải Ak để tính được số đo ái lực chung.

Cont(An,Ak,An+1)=2Bond(An,Ak)+2Bond(Ak,An+1)-2Bond(An,An+1)

=2Bond(An,Ak)

vì Bond(Ak,An+1)=Bond(An,An+1)=0

Ví dụ 3.26: Xét việc gom nhóm các thuộc tính của quan hệ PH và sử dụng ma trận ái lực AA.

Bước 1: Khởi gán

Đưa cột 1 và cột 2 của ma trận AA vào ma trận CA1

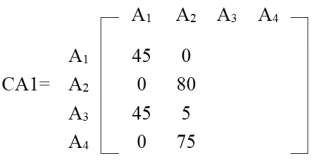
Bước 2: Lặp

Với index=3

+ Với i=1, ta tính cont(A0, A3, A1) cont(A0,A3,A1)= 2Bond(A3,A1)=

4

=2 

z1

aff (Az , A3 )aff (Az , A1 ) = 2(aff(A1,A3)aff(A1,A1)+

aff(A2,A3)aff(A2,A1)+aff(A3,A3)aff(A3,A1)+aff(A4,A3)aff(A4,A1))

=2(4548 + 50 + 5045 + 03)= 24410=8820

+ Với i=2, ta tính cont(A1,A3, A2)

cont(A1,A3,A2)= 2Bond(A1,A3)+2Bond(A3,A2)- 2Bond(A1,A2)= Bond(A1,A3)= Bond(A3,A1)= 4410

Bond(A1,A2)=450

4

Bond(A3,A2)=



z1

aff (Az , A3 )aff (Az , A2 ) = aff(A1,A3)aff(A1,A2)+

aff(A2,A3)aff(A2,A2)+aff(A3,A3)aff(A3,A2)+aff(A4,A3)aff(A4,A2)

=450 + 580 + 505 + 075 = 650 cont(A1,A3,A2)=24410+2650-2450=9920

+ Tính cont(A2,A3,A4)

+ Đưa cột 3 đặt giữa cột 1 và cột 2, cho thứ tự (1 - 3 - 2)

+ Đưa cột 3 đặt bên phải của cột 2, cho thứ tự (1- 2 - 3) và bắt đầu từ cột 3 (tức là thuộc tính A3).

Có ba nơi khác nhau để đặt cột 3: đặt bên trái của cột 1, cho thứ tự (3 - 1 - 2), đặt

giữa cột 1 và cột 2, cho thứ tự (1 - 3 - 2) và đặt bên phải của cột 2, cho thứ tự (1 - 2 - 3).

Lưu ý rằng, để tính toán sự góp phần của thứ tự cuối cùng, chúng ta phải tính

cont(A2,A3,A4), mà không phải là cont(A1,A2,A3).

Hơn nữa trong ngữ cảnh này, A4 nói đến vị trí chỉ mục thứ tư trong ma trận CA2 mà vị trí này là rỗng, không phải là cột thuộc tính A4 của ma trận AA. Chúng ta tính toán sự góp phần vào số đo ái lực chung của mỗi cách này.

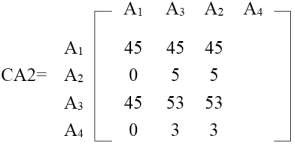
- Thứ tự (0-3-1)

cont(A1,A2,A3) = 2 bond(A0,A3) + 2 bond(A3,A1) - 2 bond(A0,A1) Chúng ta biết rằng;

bond(A0,A1) = bond(A0,A3) = 0

bond(A3,A1) = 45  45 + 5  0 + 53 + 3  0 = 4410 Do đó; cont(A1,A2,A3)= 8820

- Thứ tự (1-3-2)

cont(A1,A2,A3) = 2 bond(A1,A3) + 2 bond(A3,A2) - 2 bond(A1,A2) bond(A1,A3) = bond(A3,A1) = 4410

bond(A3,A2) = 890

bond(A1,A2) = 225

Do đó: cont(A1,A2,A3) =10150

- Thứ tự(2-3-4)

cont(A2,A3,A4) = 2 bond(A2,A3) + 2 bond(A3,A4) - 2 bond(A2,A4) bond(A2,A3) = 890

bond(A3,A4) = 0

bond(A2,A4) = 0

Do đó:cont(A2,A3,A4) = 1780

Vì sự góp phần của thứ tự (1 - 3 - 2) là lớn nhất, chúng ta đặt A3 chọn ở bên phải của A1 trong ma trận CA2.

Các tính toán tương tự cho A4 cho thấy rằng A4 nên đặt ở bên phải của A2 trong ma trận CA3.

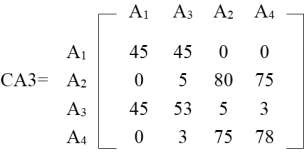
Cuối cùng, các hàng được tổ chức theo cùng thứ tự như các cột và kết quả được chỉ ra trong ma trận CA4.

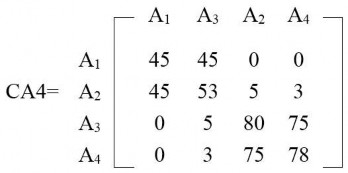
Ma trận CA4, ta thấy hình thành hai nhóm: một nhóm ở góc trái trên chứa các giá trị ái lực nhỏ hơn và một nhóm ở góc dưới phải chứa các giá trị ái lực lớn hơn. Việc

gom nhóm này cho thấy các thuộc tính của quan hệ PH được phân chia như thế nào. Tuy nhiên nói chung, ranh giới trong việc phân chia này không rò ràng. Khi ma trận CA có kích thước lớn, thông thường hình thành hơn hai nhóm và có nhiều cách phân chia. Do đó, cần phải tiếp cận vấn đề này một cách có hệ thống.

3.4.4. Giải thuật phân tách

Mục tiêu của việc phân tách là tìm các tổ hợp thuộc tính được truy xuất đơn độc hoặc phần lớn, bởi các tập hợp ứng dụng riêng biệt. Ví dụ hai thuộc tính A1 và A2 được truy xuất riêng biệt bởi ứng dụng q1 và các thuộc tính A3 và A4 được truy xuất bởi ứng dụng q3 và q4 thì dễ dàng chọn các mảnh như thế nào. Vấn đề đặt ra là tìm phương pháp mang tính giải thuật để xác định các nhóm này.

Xét ma trận thuộc tính gom tụ PA.

Nếu một điểm dọc theo đường chéo được cố định thì hai thuộc tính được xác định. Một tập hợp từ { A1, …, Ai} ở góc trái trên và tập hợp thứ hai {Ai+a, …, An} ở góc phải dưới của điểm này. Chúng ta gọi tập hợp đầu tiên là tập hợp đỉnh ( top) được ký hiệu là TA, và tập hợp thứ hai là tập hợp đáy (bottom) được ký hiệu là BA.

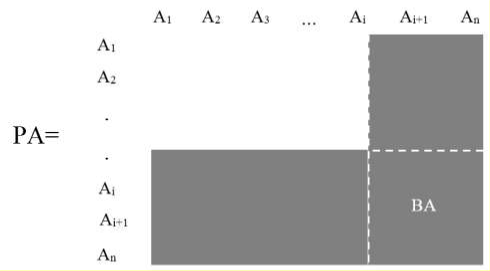
Bây giờ chúng ta đề cập đến tập hợp các ứng dụng Q={ q1, q2,…, qq}. Định nghĩa tập hợp các ứng dụng chỉ truy xuất TA, chỉ truy xuất BA, hoặc cả hai. Các tập hợp này được định nghĩa như sau:

AQ(qi)= {Ai|use(qi, Aj) =1}

TQ= { qi|AQ(qi) BQ= {qi| AQ(qi)

TA}

BA }

OQ= Q - { TQ BQ }

Công thức đầu tiên được định nghĩa tập hợp các thuộc tính được truy xuất bởi ứng dụng qi. TQ là tập hợp các ứng dụng chỉ truy xuất TA và BQ là tập hợp các ứng dụng chỉ truy xuất BA, và OQ là tập hợp các ứng dụng truy xuất cả hai TA và BA.