Cách Giải Quyết Của Chuong B. Do Và Kazutaka Katoh‌

- Làm tương tự bước 1.3 với cây Tree2 ta được đa chuỗi thẳng hàng MSA2.

Phần 3: Refinement. Tìm phương án tốt nhất.

- Bước 3.1 Một cạnh được chọn từ Tree2 (cạnh được chọn bằng cách giảm dần khoảng cách tới gốc)

- Bước 3.2 Chia cây Tree2 thành 2 phần bằng cách bỏ cạnh vừa chọn, sau đó tính lại các profile trên mỗi phần đó.

- Bước 3.3 Tạo ra một đa chuỗi thẳng hàng (sequences alignment) mới bằng cách sắp hàng một lần nữa 2 profile vừa được tạo ra.

- Bước 3.4 Nếu điểm SP (sum of pair)[23] được cải thiện thì cách sắp hàng mới được giữ lại, ngược lại ta bỏ đi.

- Lặp lại các bước 3.1-3.4 cho tới khi hội tụ hoặc đi tới giới hạn do người sử dụng định nghĩa[15].

2.3 MAFFT‌

Có thể bạn quan tâm!

• Các phương sai sắp hàng đa chuỗi nhanh - 1
• Các phương sai sắp hàng đa chuỗi nhanh - 2
• Dữ Liệu Với Số Lượng Chuỗi Lớn ( > 200 Chuỗi)
• Các phương sai sắp hàng đa chuỗi nhanh - 5
• Các phương sai sắp hàng đa chuỗi nhanh - 6

Xem toàn bộ 50 trang tài liệu này.

2.3.1 Bắt cặp nhóm sử dụng FFT

Biểu diễn một amino acid dưới dạng một vector

Tần suất của sự thay thế các amino acid phụ thuộc mạnh mẽ vào các thuộc tính lí hóa của chúng, đặc biệt là các thuộc tính khối lượng (volume) và độ phân cực (polarity)[16]. Do đó để biểu diễn một amino acid a dưới dạng vector thì ta cần một vector trong đó các thành phần của vector này là v(a) – thể hiện thuộc tính khối lượng và p(a) – thể hiện thuộc tính độ phân cực[17]. Ở đây, MAFFT[4] đã sử dụng các giá trị v(a) và p(a) đã được chuẩn hóa để thuận lợi cho việc tính toán sau này. Công thức xác định các giá trị chuẩn hóa đó là:

v

vˆ(a) v(a) v / 

p

pˆ(a) p(a) p/ 

Trong dó các giá trị v và p là các giá trị trung bình, các giá trị ,

v p

tiêu chuẩn.

là độ lệch

Khi đó một chuỗi amino acid sẽ được chuyển thành một chuỗi các vector.

Tính toán mối quan hệ giữa hai chuỗi amino acid

Mối tương quan về mặt khối lượng giữa 2 chuỗi amino acid được tính theo công thức sau

cv (k) 



1nN,1nk M

vˆ1(n)vˆ2(n k)

Trong đó N và M là độ dài của 2 amino acid.

vˆ1(n), vˆ2(n)

là giá trị của thuộc tính

khối lượng của 2 amino acid tại vị trí thứ n. k là độ trễ trong phép tính. Việc định nghĩa

k sẽ được nêu ở phần sau.

Bằng một cách hoàn toàn tương tự ta sẽ tính được giá trị

cp (k) . Khi đó hàm quan

hệ giữa 2 chuỗi amino acid này được định nghĩa theo công thức

c(k) = cv(k) + cp(k).

Nếu ta coi N = M trong trường hợp trên, khi đó độ phức tạp của thuật toán để tính mối quan hệ này là O(N2). Tuy nhiên, dựa vào biến đổi Fourier ta có thể tối ưu bước này và giảm độ phức tạp thuật toán xuống còn O(N logN) [18]. Xét với trường hợp tính toán cv(k), ta coi V1(m) và V2(m) là dạng biến đổi của v1(n) và v2(n) ta sẽ có

vˆ1(n) V1(m)

vˆ2(n) V2(m)

Ta coi dấu dùng để biểu diễn các cặp khi sử dụng Fourier và dấu * thể hiện sự chuyển vị ma trận. Khi đó giá trị của hàm phụ thuộc sẽ được tính theo công thức

c (k) V*(m)V (m)

v 1 2

Tìm kiếm đoạn tương đồng

Độ trễ k giữa hai chuỗi là độ chậm của chuỗi thứ nhất với chuỗi thứ 2. Ở phần B hình dưới đây biểu diễn độ trễ k giữa 2 chuỗi 1 và 2

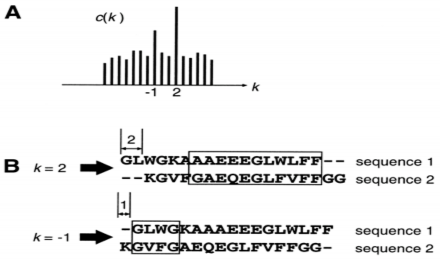
Hình 3: Ví dụ về độ trễ [4]

Bằng thực nghiệm ta thấy, với các giá trị c(k) lớn, đồng nghĩa với việc tại độ trễ đó có thể xuất hiện các chuỗi tương đồng (như trên hình vẽ). Khi đó thuật toán sử dụng một bảng trượt với độ lớn của bảng là 30 amino acid (trong hình ví dụ thì độ lớn của bảng là 4). Sau đó lấy 20 giá trị độ trễ k có c(k) lớn nhất. Sử dụng bảng trượt trên hai chuỗi này, nếu tỉ lệ tương đồng vượt quá giới hạn (giá trị giới hạn mặc định là 0.7) thì coi như ta đã tìm được một vùng tương đồng, nếu có nhiều vùng tương đồng liên tiếp với nhau thì nối chúng lại với nhau. Tuy nhiên độ lớn của vùng tương đồng này không vượt quá 150 amino acid, nếu lớn hơn 150 thì phải tách chúng ra làm 2 đoạn tương đồng.

Tạo ma trận tương đồng

Sau khi đã tìm ra được các cặp đoạn tương đồng giữa 2 chuỗi. Khi đó ta định nghĩa một ma trận hai chiều là ma trận tương đồng như sau:

Ma trận S(i,j) (i, j = 1 … n) – n là số đoạn tương đồng giữa h chuỗi.

Tại S(i, j) nếu đoạn i của chuỗi một tương đồng với đoạn j của chuỗi hai thì điểm

S(i,j) sẽ là điểm được tính như trên. Trường hợp còn lại S(i,j) = 0.

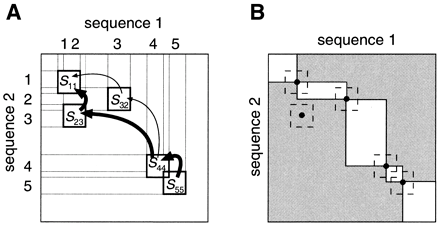
Hình 4: Ví dụ về việc tạo ma trận tương đồng [4]

Hình trên là một ví dụ của việc tạo ma trận tương đồng với 5 đoạn tương đồng giữa chuỗi 1 và chuỗi 2. Việc chọn đường đi tối ưu phụ thuộc vào S(2,3) và S(3,2). Nếu S(2,3) có giá trị lớn hơn thì đường đi sẽ theo đường in đậm như hình vẽ.

Mở rộng từ bắt cặp giữa 2 sequence thành bắt cặp nhóm

Ta có thể dễ dàng mở rộng tính toán bắt cặp giữa 2 chuỗi thành bắt cặp giữa 2 nhóm bằng cách thay công thức tính cv(k) và cp(k) với vi(n) và pi(n) bằng:

vˆgroup1(n) 

igroup1

pˆgroup1(n) 

wi.vˆi(n)

wi.pˆi(n)

igroup1

Trong đó wi là trọng số của chuỗi i trong group1

Đặc biệt, trong trường hợp sử dụng cho các nucleotide chúng ta có thể áp dụng công thức sau để tính toán hàm quan hệ:

c(k) = cA(k) + ct(k) + cc(k) + cg(k).

2.3.2 Hệ thống tính điểm

Ma trận điểm:

Để nâng cao hiệu năng của việc bắt cặp, một hệ thống tính điểm (ma trận tương đồng và điểm phạt gap) đã được sửa đổi [19]. Ma trận điểm cho thuật toán được định nghĩa theo công thức :

M

ˆ Mabaverage2/average1 average2S

a

ab

ab

Trong đó:

a, b là hai amino acid

các giá trị average được tính average1 a fa Maa average2 a,b fa fb Mab

Mab là ma trận ban đầu, mặc định ở đây là ma trận PAM 200 [15].

fa là tần số xuất hiện của amino acid a [15].

Sa là tham số thêm vào.

Đối với các acid nucleic ta có các giá trị fa = 0.25 và Sa = 0.06

Điểm phạt

Công thức tính điểm phạt được định nghĩa theo công thức:

G(i, j) Sop1 gstart ( j) gend (i)/ 2

Trong đó:

Sop là điểm phạt khi tạo ra một gap

gstart(j) là số gap xuất hiện bắt đầu từ vị trí thứ j gend(i) là số gap xuất hiện từ vị trí bắt đầu cho tới i

gstart ( j) 

w a ( j)z

( j 1)

m m m

mgroup

gend (i) 

w a (i)z (i 1)

m m m

mgroup

zm(i) = 1 và am(i) = 0 nếu tại vị trí thứ i của chuỗi có gap ngược lại zm(i)= 0 và

am(i) = 1.

2.4 PROBCONS‌

PROBCONS[5] sử dụng mô hình Markov ẩn [20] cho thuật toán progressive. Điểm khác biệt chính giữa PROBCONS[5] và các phương án tiếp cận khác đó chính là việc sử dụng ước lượng chuẩn xác cực đại (maximum expected accuracy) chứ không phải là cách sử dụng mô hình Viterbi[21], ngoài ra PROBCONS[5] còn sử dụng ước lượng các phép biến đổi để bảo toàn thông tin của các chuỗi trong khi bắt cặp. Mặt khác PROBCONS[5] còn sử dụng ma trận chuyển đổi chuẩn BLOSUM62[22] và điểm phạt phát sinh khi thêm dấu cách trong việc bắt cặp cũng được huấn luyện bởi ước lượng cực đại.

Các bước thực hiện của thuật toán PROBCONS[5] như sau: Cho m chuỗi, S = {S(1) ,… , S(m)}

- Bước 1: Tính các ma trận xác suất:

Với mỗi cặp chuỗi x và y của S, và với mỗi

i {1,...,| x | } và

j {1,...,| y | }. Ta tính

ma trận Pxy (i, j) = P(xi ~ yj a*| x, y). Đây là xác suất ký tự xi và yj được bắt cặp với nhau trong a* - pairwise alignment được sinh ra từ mô hình HMM.

- Bước 2: Tính toán kỳ vọng của độ chính xác.

Định nghĩa kỳ vọng của độ chính xác của một bắt cặp sóng đôi (pairwise alignment) a được tạo bởi hai chuỗi x và y được tính bằng số lượng liên kết chính xác của các ký tự chia cho chiều dài của chuỗi ngắn hơn.

Ea* (accuracy(a, a*)|x, y) =1P(xi ~ yj a*| x, y)

min{| x |,| y | } xi~ yja

Với mỗi cặp chuỗi x và y ta tính toán cực đại của kỳ vọng của độ chính xác bằng phương pháp quy hoạch động và đặt E(x, y) = Ea* (accuracy(a, a*)|x, y)

- Bước 3: Ước lượng tính vững chắc của các bước chuyển đổi. Ở bước này ta ước lượng lại P(xi ~ yj a*| x, y) ở bước trên. Ở dạng ma trận chuyển đổi ta có công thức:

xy 

P’  1PxzPzy

| S | zS

- Bước 4: Xây dựng cây hướng dẫn (guide tree).

Xác định ma trận tương đồng giữa 2 chuỗi x và y bằng giá trị E(x, y) được tính ở bước 2. Từ đó ta xây dựng cây hướng dẫn.

- Bước 5: Progressive alignment

Dựa vào cây hướng dẫn được dựng từ bước 4, ta tiến hành bắt cặp.

Qua các thực nghiệm với các bộ dữ liệu chuẩn, kết quả của PROBCONS[5] là rất cao (cao nhất với rất nhiều bộ dữ liệu chuẩn). Tuy nhiên, một hạn chế cực lớn của PROBCONS[5] là tốc độ, về mặt này PROBCONS[5] không thể so sánh với các thuật toán trên.

Chương 3. Cây quyết định

3.1 Cách giải quyết của Chuong B. Do và Kazutaka Katoh‌

Như đã trình bày ở trên, hiện nay có khá nhiều phương pháp sắp hàng đa chuỗi, nhưng mỗi phương pháp lại có một đặc điểm riêng kèm theo đó là những ưu khuyết điểm riêng. Đôi khi một phương pháp cho kết quả tốt với bộ dữ liệu này, lại không phù hợp với bộ dữ liệu khác. Một phương pháp cho kết quả rất cao nhưng tốc độ lại quá chậm, hoặc không thể xử lý những dữ liệu quá lớn. Qua đó có thể thấy việc xây dựng cây quyết định để giải quyết vấn đề chọn phương pháp tối ưu nhất cho mỗi loại dữ liệu đầu vào là vô cùng quan trọng. Hai nhà khoa học Chuong B. Do và Kazutaka Katoh đã đề ra một giải pháp[26] là nghiên cứu về từng phương pháp và từng loại dữ liệu, qua đó có thể đưa ra được những phương pháp phù hợp với từng bộ dữ liệu cả về mặt điểm chuẩn lẫn thời gian xử lý.

Hai tác giả đã chia các loại dữ liệu ra thành 3 phần riêng biệt cần phải xem xét là:

- Dữ liệu yêu cầu tìm thành phần lặp.

- Dữ liệu đầu vào có số lượng chuỗi lớn ( > 200 chuỗi ).

- Dữ liệu đầu vào có chuỗi có độ dài lớn ( > 2000 amino acid).

Đối với loại dữ liệu thứ nhất, chúng ta không xem xét nó trong phạm vi của khóa luận này.

Đối với dữ liệu đầu vào có số lượng chuỗi lớn ( > 200 chuỗi ). Hai tác giả đã chỉ ra độ phức tạp thuật toán trong việc tính toán ma trận khoảng cách là nhân tố chủ yếu trong việc dẫn đến thời gian thực hiện quá lâu của các phương pháp. Cho nên những phương pháp có cách xây dựng ma trận khoảng cách với độ phức tạp thấp sẽ được chọn. Ở đây, 2 phương pháp MUSCLE và FFT-NS-2 đã được chọn.

Với dữ liệu có chuỗi có độ dài lớn ( > 2000 amino acid), thì độ phức tạp không gian của thuật toán là nguyên nhân chính dẫn đến việc thuật toán có xử lý được loại dữ liệu này không. Hầu hết các phương pháp có độ phức tạp không gian là O(L2) với L là độ dài trung bình của các chuỗi. Đối với loại dữ liệu này, những phương pháp có độ phức tạp không gian tuyến tính ( CLUSTALW, FFT-NS-1 và FFT-NS-2 ) được sử dụng.