CÇn t©y
2.2 Hạn chế đối tượng nghiên cứu
Do điều kiện khảo sát thực tế và do thời gian thực hiện luận văn có hạn, đề tài sẽ tập trung và các đối tượng sau:
Những bệnh nhân được xét đến là: đã thay 1 hoặc cả 2 van tim. Vùng miền sinh sống: ở miền Bắc Việt Nam.
Các điều kiện dịch tế khác: chỉ xét các đối tượng ở thành thị hoặc nông thôn.
Các đối tượng bệnh nhân ở thành thị thường có mức độ ổn định cao hơn sau mỗi lần
đến khám lại.
Các đối tượng ở nông thôn có những sự khác biệt lớn sau mỗi lần đến khám lại. Điều kiện nữa là: chỉ xét và theo dõi những bệnh nhân tuân thủ đúng lịch điều trị của bác sĩ.
Chương 3: Cơ sở lý thuyết một số phương pháp tính toán mềm
3.1 Lý thuyết tập mờ
Có thể bạn quan tâm!
-
Ứng dụng một số phương pháp tính toán mềm xây dựng phần mềm trợ giúp điều trị thuốc chống đông đường uống cho bệnh nhân sử dụng van tim nhân tạo - 1 -
Ứng dụng một số phương pháp tính toán mềm xây dựng phần mềm trợ giúp điều trị thuốc chống đông đường uống cho bệnh nhân sử dụng van tim nhân tạo - 2 -
Xác Định Các Yếu Tố Liên Quan Và Các Kiến Thức Chuyên Gia Trong Điều Trị Thuốc Chống Đông Đường Uống . -
Các Kỹ Thuật Lập Luận Dựa Trên Sự Sử Dụng Lại -
Ngưỡng Inr An Toàn Đối Với Từng Loại Van Nhân Tạo -
Công Thức Xác Định Các Hàm Tương Tự Thành Phần
Xem toàn bộ 91 trang tài liệu này.
3.1.1 Các khái niệm
Vµo n¨m 1965, gi¸o s− L Zadeh [8] lµ ng−êi ®µu tiªn c«ng bè mét c«ng tr×nh khoa häc vÒ hÖ mê. C«ng tr×nh cđa «ng ®· thùc sù khai sinh ra mét nghµnh khoa häc míi “ Lý thuyÕt tËp mê ” vµ nã ®· nhanh chãng ®−îc c¸c nhµ nghiªn cøu c«ng nghÖ t¸n thµnh vµ đng hé. Mét sè kÕt qu¶ b−íc ®Çu vµ c¸c h−íng nghiªn cøu tiÕp theo ®· gãp phÇn t¹o nªn nh÷ng s¶n phÈm phÇn mÒm cã ý nghÜa ®ang ®−îc sö dông kh¸ réng r·i trªn toµn cÇu.
Lý thuyÕt mê ngµy cµng phong phó vµ hoµn thiÖn, t¹o nªn mét nÒn mãng v÷ng ch¾c
®Ó ph¸t triÓn logic mê, mét c¬ së c¬ b¶n nhÊt trong trong c«ng ®o¹n m« h×nh ho¸ c¸c lËp luËn mê mµ con ng−êi vÉn th−êng xuyªn sö dông trong ®êi sèng. Cã thÓ nãi logic mê lµ chiÕc cÇu nèi ®Ó x©y dùng c¸c hÖ mê thùc tiÔn nh− c¸c bé ®iÒu khiÓn mê trong c«ng nghiÖp, c¸c hÖ chuyªn gia trong y häc trî gióp vµ chuÈn ®o¸n bÖnh, c¸c hÖ chuyªn gia xö lý tiÕng nãi, nhËn d¹ng ¶nh...
§Þnh nghÜa tËp mê
Theo lý thuyÕt tËp hîp cæ ®iÓn, khi cho tr−íc mét tËp X, A lµ tËp con cđa X vµ víi mçi mét phÇn tö x X, cã hai kh¶ n¨ng: hoÆc x A, hoÆc x A. Nh− vËy viÖc x¸c
®Þnh x cã ph¶i lµ phÇn tö cđa tËp AX t−¬ng ®−¬ng víi viÖc x¸c ®Þnh hµm ®Æc tr−ng
A tho¶ m·n [8].
A ( x )
⎧1 ,
⎩
⎨ 0 ,
x A
x A
B»ng c¸ch më réng miÒn gi¸ trÞ cđa hµm A(x) tõ hai ®iÓm rêi r¹c 0 vµ 1 thµnh ®o¹n [0,1], L.A.Zadeh ®· x©y dùng kh¸i niÖm tËp mê lµ nÒn t¶ng cđa toµn bé lý thuyÕt mê.
§Þnh nghÜa: Cho X lµ tËp hîp th−êng ®−îc gäi lµ kh«ng gian nÒn. A ®−îc gäi lµ tËp mê trªn X nÕu A={(x, A(x))|x X} trong ®ã A: X->[0,1]. Hµm A gäi lµ hµm thuéc (membership function) cđa A, A(x) lµ mét gi¸ trÞ trong ®o¹n [0,1] gäi lµ møc
®é thuéc cđa x trong A [8].
VÝ dô:
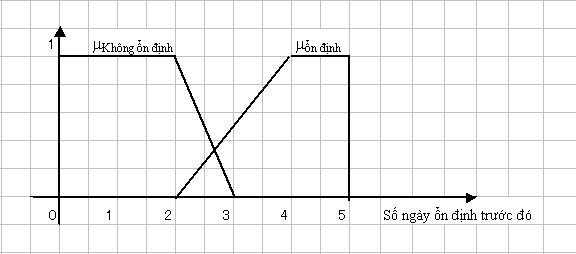
Chế độ ăn uống của người bệnh có hai trạng thái “ổn định” và “không ổn định”,
Ổn định được định nghĩa là trong 5 ngày liên tiếp trước đó, số ngày ổn định phải lớn hơn 4 ngày,
Không ổn định được định nghĩa là, trong 5 ngày liên tiếp trước đó, số ngày không
ổn định ít nhất là 2 ngày.
3.1.2 Các phép toán cơ sở
Hîp cđa hai tËp mê
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ A,
B . Hîp cđa hai tËp mê A vµ B, ký hiÖu A B, lµ mét tËp mê cã hµm thuéc AB
®−îc x¸c ®Þnh nh− sau:
Giao cđa hai tËp mê
AB(x)=max(A(x),B(x)) x X
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ A,
B. Giao cđa hai tËp mê A vµ B, ký hiÖu AB, lµ mét hµm thuéc AB x¸c ®Þnh nh− sau:
AB(x)=min(A(x), B(x)) víi x X
PhÇn bï cđa mét tËp mê
Cho A lµ tËp mê trong X cã hµm thuéc A . PhÇn bï cđa A trong X lµ mét tËp mê cã hµm thuéc sau:
A (x) 1 A (x),x X
§Þnh nghÜa n»m trong
Cho X lµ mét tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ
A, B. A gäi lµ n»m trong B, ký hiÖu AB, nÕu A(x)B(x) xX.
Hai tËp mê b»ng nhau
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ A,
B . A gäi lµ b»ng B , ký hiÖu A=B, nÕu vµ chØ nÕu A(x)= B(x) xX.
Tæng rêi cđa hai tËp hîp
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X. Tæng cđa hai tËp mê A vµ B trong X, ký hiÖu AB, lµ mét tËp mê tho¶ m·n:
A B ( A B) ( A B)
PhÐp trõ hai tËp mê
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X. PhÐp trõ hai tËp mê A vµ b, ký hiÖu AB, ®−îc ®Þnh nghÜa nh− sau:
A B A B
TÝch ®¹i sè cđa hai tËp mê
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ A,
B. TÝch ®¹i sè cđa hai tËp mê A vµ B trong E, ký hiÖu lµ A.B lµ tËp mê cã hµm thuéc tho¶ m·n:
A.B(x)=A . B x X
Tæng ®¹i sè cđa hai tËp mê
Cho X lµ tËp hîp, A vµ B lµ hai tËp mê trong X, cã c¸c hµm thuéc lÇn l−ît lµ A,
B. Tæng ®¹i sè cđa hai tËp mê A vµ B trong X, ký hiÖu A+B, lµ tËp mê cã hµm
thuéc tho¶ m·n:
A+B(x)=A(x) + B(x) - A(x). B(x) xX.
TËp hîp møc cđa tËp mê
Cho [0,1], X lµ mét tËp hîp, A lµ mét tËp mê trong X cã hµm thuéc A . TËp hîp Atho¶ m·n A={xX| A(x)} gäi lµ tËp hîp møc cđa mét tËp mê A.
Tõ ®Þnh nghÜa trªn chóng ta cã tÝnh chÊt sau: gi¶ sö 1, 2 [0,1] vµ 12 . Khi ®ã A1 A2 .
3.1.3 Mô hình mờ và phương pháp lập luận mờ
M« h×nh mê vµ ph−¬ng ph¸p lËp luËn mê ®−îc Zadeh ®Ò xuÊt. Sau ®ã mét sè nhµ nghiªn cøu ®· ph¸t triÓn tiÕp ý t−ëng cđa Zadeh vµ ®Ò xuÊt mét sè ph−¬ng ph¸p lËp luËn mê míi [12,13,14].
M« h×nh mê gåm n mÖnh ®Ò IF-THEN if X=A1 then Y=B1
if X=A2 then Y=B2
...
if X=An then Y=Bn
trong ®ã X,Y lµ c¸c biÕn th«ng th−êng ch¼ng h¹n nh− c−êng ®é dßng ®iÖn, tèc ®é quay cđa ®éng c¬, tuæi cđa ng−êi,...) Ai, Bi i=1,..,n lµ c¸c m« t¶ ng«n ng÷ cđa c¸c biÕn X,Y ch¼ng h¹n nh− c−êng ®é dßng ®iÖn “t−¬ng ®èi nhá”, tèc ®é quay cđa ®éng c¬ ®iÖn “kh¸ nhanh”. Trong m« h×nh nµy tÊt c¶ c¸c biÕn ng«n ng÷ Ai, Bi i=1,...,n
®−îc biÓu diÔn b»ng c¸c tri thøc mê. Môc ®Ých cđa m« h×nh mê nh»m suy ra th«ng
tin mê cđa biÕn Y tõ c¸c th«ng tin mê cđa biÕn X vµ qu¸ tr×nh nµy ®−îc gäi lµ qu¸ tr×nh mê.
Ph−¬ng ph¸p lËp luËn trªn m« h×nh mê ®−îc c¨n cø vµo n mÖnh ®Ò IF-THEN cđa m« h×nh mê. NÕu ta cã mÖnh ®Ò vµo “X=A” th× sÏ suy ra ®−îc mÖnh ®Ò kÕt luËn lµ “Y=B” dùa vµo c¸c mÖnh ®Ò sau cđa m« h×nh
MÖnh ®Ò 1 If X=A1 then Y=B1 MÖnh ®Ò 2 If X=A2 then Y=B2
....
MÖnh ®Ò n If X=An then Y=Bn MÖnh ®Ò If X=A
KÕt luËn Y=B
Qu¸ tr×nh tÝnh to¸n trong lËp luËn mê gåm hai b−íc: tr−íc hÕt x©y dùng mét quan hÖ mê R gi÷a hai biÕn X vµ Y, sau ®ã tõ th«ng tin mê cđa biÕn X suy ra th«ng tin mê cđa biÕn Y dùa vµo R. §Ó x©y dùng quan hÖ mê R, tr−íc hÕt mçi luËt IF-THEN
®−îc chuyÓn thµnh c¸c quan hÖ mê Ri (i=1,2...,n) t−¬ng øng, sau ®ã n quan hÖ mê nµy ®−îc tæng hîp víi nhau theo mét c¸ch nµo ®ã ®Ó cã quan hÖ mê R. Nãi mét c¸ch kh¸c, ta cã c¸c to¸n tö vµ ®Ó thùc hiÖn qu¸ tr×nh tr×nh tÝnh to¸n sau:
Ai, Bi lµ c¸c tËp mê,
Ai Bi =Ri
R1 R2 ...Rn=R
Ri (i=1,..n) vµ R lµ c¸c quan hÖ mê.
C¸c to¸n tö vµ , trong mét sè tr−êng hîp, sÏ ®−îc chän t−¬ng øng lµ hµm OR vµ AND cđa logic mê.
Sau khi x©y dùng ®−îc quan hÖ mê R nªu trªn chóng ta chuyÓn sang b−íc thø hai cđa qu¸ tr×nh tÝnh to¸n: víi bÊt kú tËp mê A nµo m« t¶ biÕn X chóng ta lu«n x¸c
®Þnh ®−îc tËp mê B m« t¶ biÕn Y b»ng c¸ch hîp thµnh A víi quan hÖ R B=AR
KÕt thóc qu¸ tr×nh trong lËp luËn mê chóng ta cã tËp mê B m« t¶ vÒ biÕn th«ng th−êng Y, tøc lµ cã mÖnh ®Ò “Y=B”.
3.1.4 Khử mờ
Khö mê lµ ph−¬ng ph¸p −íc l−îng gi¸ trÞ cđa biÕn th«ng th−êng tõ tËp mê m« t¶ biÕn ®ã. Gi¶ sö B lµ tËp mê m« t¶ biÕn th«ng th−êng Y víi hµm thuéc B(b). Cã nhiÒu ph−¬ng ph¸p khö mê ®Ó tÝnh Y tõ B. Chóng ta h·y xem xÐt mét sè ph−¬ng ph¸p khö mê ®−îc m« t¶ d−íi ®©y.
Ph−¬ng ph¸p lÊy träng t©m
§©y lµ ph−¬ng ph¸p ®−îc sö dông réng r·i nhÊt trong ®iÒu khiÓn mê. C¸ch khö mê nh− sau:
m
bi.B(bi)
m
Y i 1,bi B,i 1,..., m
B(bi)
i 1
Ph−¬ng ph¸p lÊy trung b×nh c¸c ®iÓm cùc ®¹i
n
bi
Y i 1,bi B,i 1,..., n n
trong ®ã n lµ sè ®iÓm cùc ®¹i cđa B(b), bi lµ c¸c ®iÓm hµm B(b) ®¹t cùc ®¹i.
Ph−¬ng ph¸p ®iÓm gi÷a cđa c¸c ®iÓm cùc ®¹i
Lµ ph−¬ng ph¸p thu gän tõ ph−¬ng ph¸p trªn.
trong ®ã b’ lµ ®iÓm bÐ nhÊt mµ B(b) ®¹t cùc ®¹i, b’’ lµ ®iÓm lín nhÊt mµ B(b) ®¹t cùc ®¹i.
Y 1 (b'b'')
2