GA-M | R-CSM | |||||
Best | Avg | Std | Best | Avg | Std | |
200_40_90_9 | 130 | 133 | 3.0 | 112 | 125 | 12.6 |
200_40_91_15 | 133 | 139 | 5.8 | 117 | 127 | 9.1 |
Có thể bạn quan tâm!
-
Một số phương pháp gần đúng giải bài toán lập lịch với tài nguyên giới hạn - 13 -
Ý Tưởng Của Phương Pháp Thích Nghi -
Đánh Giá Chất Lượng Lời Giải Của Thuật Toán -
Đánh Giá Chất Lượng Lời Giải Của Thuật Toán -
Một số phương pháp gần đúng giải bài toán lập lịch với tài nguyên giới hạn - 18 -
Một số phương pháp gần đúng giải bài toán lập lịch với tài nguyên giới hạn - 19
Xem toàn bộ 156 trang tài liệu này.
Bảng 4.10: Kết quả thực nghiệm R-CSM với bộ dữ liệu TNG
GA | R-CSM | |||||
Best | Avg | Std | Best | Avg | Std | |
TNG1 | 201 | 203 | 3.5 | 131 | 136 | 4.5 |
TNG2 | 198 | 205 | 8.3 | 133 | 138 | 5.2 |
TNG3 | 212 | 218 | 7.1 | 132 | 135 | 1.6 |
TNG4 | 176 | 187 | 11.3 | 127 | 134 | 7.6 |
TNG5 | 751 | 757 | 6.2 | 572 | 577 | 4.1 |
TNG6 | 791 | 796 | 5.5 | 626 | 636 | 8.5 |
TNG7 | 810 | 820 | 10.7 | 569 | 573 | 5.7 |
TNG8 | 720 | 728 | 9.4 | 560 | 564 | 3.6 |
4.3.3. Đánh giá chất lượng lời giải của thuật toán
Các thực nghiệm được triển khai trên 02 thuật toán GA-M và R-CSM, mỗi thuật toán thực hiện trên bộ dữ liệu iMOPSE và bộ dữ liệu TNG. Kết quả thực nghiệm được trình bày trong bảng 4.9 và bảng 4.10 chỉ ra thuật toán R-CSM có chất lượng lời giải luôn tốt hơn thuật toán GA-M.
Với bộ dữ liệu iMOPSE, giá trị tốt nhất của R-CSM tốt hơn GA-M từ 0,04% đến 23,1 %, so sánh chi tiết được thể hiện trong hình 4.8. Tổng độ lệch chuẩn của GA-M là 163,1, của R-CSM là 122,1, điều này cho thấy độ ổn định của thuật toán R-CSM tốt hơn, hình 4.9 cho so sánh độ lệch chuẩn giữa R-CSM và GA-M.
Với bộ dữ liệu TNG (thông số thực nghiệm trong bảng 4.10), giá trị tốt nhất của R-CSM tốt hơn GA-M từ 20,86% đến 37,74%, so sánh chi tiết được thể hiện trong hình 4.10. Tổng độ lệch chuẩn của GA-M là 62, của R-CSM là 40,8, điều này cho thấy độ ổn định của thuật toán R-CSM tốt hơn, hình 4.11 cho so sánh độ lệch chuẩn giữa R-CSM và GA-M.
111
4.3.4. Hình ảnh so sánh R-CSM với thuật toán GA-M
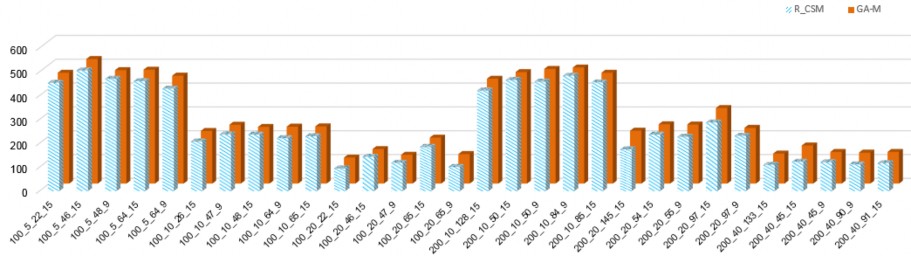
Hình 4.8. So sánh giá trị BEST giữa R-CSM với GA-M trên iMOPSE
Hình 4.9. So sánh giá trị STD giữa R-CSM với GA-M trên iMOPSE
Hình 4.10. So sánh giá trị BEST giữa R-CSM, GA-M và TNG trên
Hình 4.11. So sánh giá trị STD giữa R-CSM với GA-M
4.4. Đề xuất thuật toán RR-CSM
Trong thực tế, khi thực hiện xong một tác vụ, tài nguyên có thể ở vào trạng thái trống (rảnh rỗi), tác vụ kế tiếp chưa thực hiện được ngay vì phải chờ tác vụ khác thực hiện xong, có thể bởi các tài nguyên khác. Do vậy, để tận dụng tài nguyên, thuật toán đề xuất sẽ áp dụng hàm Rotate() để tìm các khoảng thời gian mà tài nguyên rảnh rỗi để bố trí thực hiện tác vụ. Hàm Rotate() chính là cải tiến mới của thuật toán RR-CSM (Rotate and Reallocate Cuckoo Search for MS- RCPSP) so với thuật toán R-CSM ở mục trước.
4.4.1. Phương pháp Rotate
Các tác vụ trong dự án được thực hiện theo một thứ tự ưu tiên cho trước, đây là một ràng buộc của bài toán MS-RCPSP và Real-RCPSP. Khi xây dựng lịch biểu, các tác vụ sẽ được thiết lập tài nguyên thực hiện, số lượng tài nguyên thực hiện các tác vụ là hạn chế. Nói cách khác, để hoàn thành dự án, một tài nguyên sẽ phải thực hiện nhiều tác vụ theo thứ tự ưu tiên nhất định. Có 02 trường hợp có thể xảy ra:
- Các tác vụ ràng buộc thứ tự ưu tiên được thực hiện bởi cùng 01 tài nguyên, ví dụ như trong hình 4.14.a. Khi đó tài nguyên sẽ được sử dụng liên tục không có thời gian trống.
- Các tác vụ ràng buộc thứ tự ưu tiên được thực hiện bởi các tài nguyên khác nhau, ví dụ hình 4.14.b Trong trường hợp này, có thể xảy ra tình trạng tài nguyên rỗi do phải chờ tác vụ trước hoàn thành trên tài nguyên khác.
Ví dụ 4.5:
Xét 02 dự án, mỗi dự án có 10 tác vụ, với đồ thị ưu tiên của các tác vụ được thể hiện lần lượng trong hình 4.12 và hình 4.13.
1 2 3 4 5 7 8 9 6 10 | |
Hình 4.12. Đồ thị ưu tiên của dự án 1 | Hình 4.13. Đồ thị ưu tiên của dự án 2 |
Thời gian thực hiện của các tác vụ được thể hiện trong bảng 3.11 dưới đây.
Bảng 4.11: Thời gian thực hiện các tác vụ
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Thời gian | 2 | 3 | 5 | 2 | 4 | 3 | 6 | 2 | 4 | 2 |
Để thực hiện mỗi dự án, sử dụng tập tài nguyên L = {L1, L2}, với năng lực
của các tài nguyên như sau:
L1 = {W1,W2,W4,W5,W7,W8,W9,W10}
L2 = {W1,W3,W6,W7,W8,W9}
Căn cứ trên đồ thị ưu tiên của 02 dự án, ta có thể xây dựng 02 lịch biểu cho mỗi dự án với biểu đồ Gantt của lịch biểu lần lượt trong hình 4.14.a và hình 4.14.b.
Time (b). Các tài nguyên có khoản thời gian trống Hình 4.14. Các tài nguyên sử dụng liên tục (a) và có thời gian trống (b) |
Theo thứ tự ưu tiên như trong hình 4.13, tác vụ W6 chỉ được thực hiện sau khi tác vụ W5 hoàn thành trên tài nguyên L1. Do W6 được thực hiện bởi L2, nên thời gian bắt đầu thực hiện W6 cần lùi lại đến giờ thứ 12 (sau khi W5 kết thúc trên L1), điều này tạo ra khoảng thời gian rỗi của L2 từ giờ thứ 8 đến hết giờ thứ 11.
4.4.1.1. Ý tưởng của phương pháp Rotate
Phương pháp Rotate nhằm hạn chế tối đa khoảng thời gian rỗi của tài nguyên, dẫn đến giảm tổng thời gian thực hiện dự án. Các bước thực hiện cụ thể như sau:
- Bước 1: Tìm tài nguyên sử dụng nhiều nhất trong Cbest, gọi là Lb. Đây là tài nguyên kết thúc công việc sau cùng trong các tài nguyên sử dụng để thực hiện dự án.
- Bước 2: Duyệt các tác vụ được thực hiện bởi Lb theo thứ tự ngược với thứ tự thực hiện từ phải qua trái trên tài nguyên, tức là tác vụ nào thực hiện sau sẽ xem xét trước.
WRb: tập tác vụ vụ đang được thực hiện bởi Lb
- Bước 3: Với mỗi tác vụ Wi ∈ WRb (i= sizeof(WRb) downto 1), thực hiện:
• Bước 3.1: Tìm khoảng thời gian rỗi trên tài nguyên
• Bước 3.2: Chuyển thứ tự thực hiện của tác vụ hiện tại về vị trí của tài nguyên rỗi nếu không vi phạm ràng buộc về thứ tự ưu tiên.
• Bước 3.3: Điều chỉnh thời gian bắt đầu và kết thúc thực hiện của các tác vụ có vị trí thực hiện sau vị trí mới của tác vụ hiện tại
• Bước 3.4: Tính toán lại makespan của dự án, nếu tạo ra cá thể tốt hơn thì dừng thuật toán.
Về bản chất, phương pháp Rotate là cách tái sắp xếp thứ tự thực hiện các tác vụ trên tài nguyên hoàn thành công việc sau cùng mà không vi phạm các ràng buộc về thứ tự ưu tiên giữa các tác vụ, đồng thời hạn chế tối đa thời gian tài nguyên rỗi. Việc này giúp giảm tổng thời gian thực hiện dự án đáng kể.
Ví dụ 4.6:
Xem xét lịch biểu được biểu diễn trong hình 4.14.b, lịch biểu này có makespan là 20. Trong lịch biểu thể hiện:
Lb: là tài nguyên L2
WR2 = {W3, W6, W8, W9}
Áp dụng phương pháp Rotate, ta có thể chuyển thứ tự thực hiện của W9 từ vị trí thực hiện cuối cùng, thời gian bắt đầu ở vị trí giờ thứ 16 chuyển lên vị trí thực hiện mới sau W3 với thời gian thực hiện bắt đầu ở vị trí giờ thứ 7. Phép dịch chuyển vị trí này vẫn đảm bảo được ràng buộc ưu tiên như trong hình 4.12.
Sau phép dịch chuyển, makespan của lịch biểu giảm từ 20 còn 19. Chi tiết quá trình này được thể hiện trong hình 4.15.
Trước Rotate
Sau Rotate
Ti
Hình 4.15. Biểu đồ Gantt khi áp dụng phương pháp Rotate
4.4.1.2. Hàm Rotate
Phương pháp Rotate áp dụng cho các cá thể trong bài toán Real-RCPSP được trình bày chi tiết trong Algorithm 4.4 sau đây.
Input: currentBest (các thể tốt nhất sau mỗi thế hệ) Output: lịch biểu sau khi được hiệu chỉnh |
1. makespan = f(currentBest) 2. newbest = currentBest; 3. Lb ← lastResource (newbest) //tài nguyên hoàn thành sau cùng 4. Wb ← {các task vụ được thực hiện bởi Lb} 5. For i = size(WRb) downto 1// duyệt lần lượt từng task 6. freepos ← Vị trí tài nguyên rỗi 7. If (freepos >0) 8. Begin 9. newbest = { 10. Wi thực hiện tại vị trí freepos 11. Tính toán lại vị trí thực hiện của các task khác 12. } 13. newmakespan = f(newbest) // tính toán lại makespan 14. If newmakespan < makespan 15. makespan = newmakespan 16. Return newbest; // dịch chuyển thành công, trả về kết quả và dừng hàm |
Với: - f: hàm tính makespan của một lịch biểu - size: hàm tính số phần tử của một tập/mảng - lastResource: hàm trả về tài nguyên kết thúc thực hiện sau cùng |
4.4.2. Thuật toán
Cuckoo Search [60],[61] là thuật toán tiến hóa áp dụng cho việc giải các bài toán thuộc lớp NP-Khó và mang lại hiệu quả tốt. CS dịch chuyển quần thể bằng phép nhảy Lévy Flight với 02 kỹ thuật tìm kiếm: tìm kiếm cục bộ (Local Search) và tìm kiếm toàn cục (Global Search), hai phép tìm kiếm này giúp CS mở rộng được không gian tìm kiếm, thoát khỏi được cực trị địa phương.
Thuật toán RR-CSM xây dựng trên nền tảng của CS và áp dụng trong việc giải bài toán Real-RCPCP. RR-CSM thực hiện qua các bước như sau:
- Bước 1: Khởi tạo quần thể với n cá thể: Pall
- Bước 2: Tính toán các giá trị trong quần thể: cá thể tốt nhất bestnest, giá trị tốt nhất của mỗi cá thể trong quần thể qua các thế hệ (fitness), …
- Bước 3: Thực hiện các tiến hóa qua các thế hệ
- Bước 4: Với mỗi thế hệ, thực hiện
- Bước 4.1: Tạo ra 01 cá thể mới bằng kỹ thuật GS, cá thể mới là: Pnew
- Bước 4.2: Chọn Pi ngẫu nhiên từ quần thể
𝑃𝑖
= { 𝑃𝑛𝑒𝑤 𝑖𝑓 𝑓(𝑃𝑛𝑒𝑤) < 𝑓(𝑃𝑖)
𝑃𝑖 𝑖𝑓 𝑓(𝑃𝑛𝑒𝑤) ≥ 𝑓(𝑃𝑖)
- Bước 4.3: Tính toán các giá trị trong quần thể: bestnest, fitness, …