ra là mức tỷ số SNR có hiệu quả trong các môi trường này là 5 đến 15 dB. Mức độ âm của nhiễu rất cao trong các môi trường ở tàu điện ngầm, ở trên máy bay, nó đạt khoảng 70 đến 75 dB SPL. Và mức độ âm của tiếng nói trong các môi trường này cũng đạt mức đó, nên mức tỷ số SNR trong các môi trường này gần như là 0 dB.
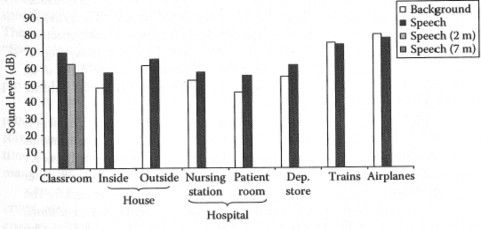
Hình 1.5 Mức nhiễu và tiếng nói (được đo bằng SPL dB) trong các môi trường
khác nhau.
1.5 TÍN HIỆU RỜI RẠC THEO THỜI GIAN
Tín hiệu rời rạc theo thời gian x(n) có thể tạo ra bằng cách lấy mẫu tín hiệu liên tục theo thời gian xa(t) với chu kỳ lấy mẫu là Ts (tần số lấy mẫu Fs = 1/ T). Ta có
xa(t)|t=nT = xa(nT) = x(n) , -∞ < n< ∞ (1.1)
Lưu ý n là biến nguyên, x(n) là hàm theo biến nguyên, chỉ định tại các giá trị n nguyên. Khi n không nguyên, thì x(n) không xác định, chứ không phải bằng 0. Trong nhiều sách về xử lý tín hiệu số, người ta quy ước: khi biến nguyên thì biến được đặt trong dấu ngoặc vuông và khi biến liên tục thì được đặt trong dấu ngoặc tròn. Từ đây trở đi, ta ký hiệu tín hiệu rời rạc là: x[n].
Một số tín hiệu rời rạc cơ bản:
Có thể bạn quan tâm!
-
Áp dụng thuật toán Wiener Filtering nâng cao chất lượng tiếng nói - 1 -
Áp dụng thuật toán Wiener Filtering nâng cao chất lượng tiếng nói - 2 -
Thang Điểm Đánh Giá Chất Lượng Tiếng Nói Theo Mos -
Overlap Và Adding Trong Quá Trình Xử Lý Tín Hiệu Tiếng Nói -
Thực Hiện Xử Lý Các File Âm Thanh Bị Nhiễu Với Snr =5Db
Xem toàn bộ 69 trang tài liệu này.
1.5.1 Tín hiệu bước nhảy đơn vị
u[n] =
1, n 0
2, n 0
(1.2)
Tín hiệu bước nhảy dịch chuyển có dạng sau:
1.5.2 Tín hiệu xung đơn vị
u[n - no] =
1,
0,
n no n no
(1.3)
[n]1,
0,
n 0
n 0
(1.4)
Tín hiệu xung dịch chuyển có dạng sau
[nno] 1,
0,
n no n no
(1.5)
Chúng ta có thể biểu diễn tín hiệu rời rạc theo thời gian x[n] thông qua tín hiệu xung đơn vị như sau
1.5.3 Tín hiệu hàm mũ
x[n] = x[k][n k]
k
(1.6)
x[n] = C.an (C,a : là những hằng số) (1.7) Tín hiệu hàm mũ phía phải : x[n] = C.an.u[n]
Tín hiệu hàm mũ phía trái : x[n] = C.an.u[-n]
1.5.4 Tín hiệu hàm sin rời rạc
x[n] Acos(2fn)
A : là biên độ của tín hiệu sin
: pha ban đầu của tín hiệu sin
n
(1.8)
f : tần số số, f =
F , F : là tần số của tín hiệu, Fs : tần số lấy mẫu
Fs
-0.5 < f < 0.5
1.6 PHÉP BIẾN ĐỔI FOURIER CỦA TÍN HIỆU RỜI RẠC DTFT
Phép biến đổi này áp dụng để phân tích cho cả tín hiệu và hệ thống. Nó được dùng trong trường hợp dãy rời rạc dài vô hạn và không tuần hoàn.
DTFT :
X () x[n]ejn n
(1.9)
Ta nhận xét thấy rằng tuy tín hiệu rời rạc trong miền thời gian nhưng DTFT lại liên tục và tuần hoàn trong miền tần số.
DTFT chính là hàm phức theo biến tần số thực. Ta gọi DTFT là phổ phức (complex spectrum) hay ngắn gọn là phổ của tín hiệu rời rạc x[n].
1.6.1 Sự hội tụ của phép biến đổi Fourier
Không phải là tất cả DTFT đều tồn tại (hội tụ) vì DTFT chỉ hội tụ khi
x[n]ejn
n
(1.10)
Ta luôn luôn có :
x[n]ejn n
x[n]ejn n
x[n]ejn n
x[n]ejn n
| x[n] || ejn |
n
| x[n] |
n
(1.11)
Như vậy, nếu x[n] thoả điều kiện | x[n] | < thì biến đổi Fourier hội tụ.
n
1.6.2 Quan hệ giữa biến đổi Z và biến đổi Fourier
Biểu thức tính ZT là:
X (z) x[n]z n n
(1.12)
Giả sử ROC có chứa đường tròn đơn vị. Tính X(Z) trên đường tròn đơn vị, ta
được
X (z)
ze
x[n]e X ()
jn
j
n
(1.13)
Như vậy, biến đổi Fourier chính là biến đổi Z tính trên đường tròn đơn vị. Dựa vào đây, ta có thể phát biểu lại điều kiện tồn tại của DTFT như sau :
Biến đổi Fourier của một tín hiệu chỉ tồn tại khi ROC của biến Z của tín hiệu đó có chứa đường tròn đơn vị.
1.6.3 Phép biến đổi Fourier ngược
- Biểu thức tính biến đổi Fourier ngược
Ta thấy X( ) là một hàm tuần hoàn với chu kỳ
2
2, do e jtuần hoàn với chu kỳ
e je j (2) e je j 2
e j
(1.14)
Do đó dải tần số của tín hiệu rời rạc là một dải tần bất kỳ rộng 2 , thường chọn
là: (,) hay (0,2 ).
Vậy ta có thể khai triển X( ) thành chuỗi Fourier trong khoảng ( ,) hay (0,2) nếu điều kiện tồn tại của X( ) thoả mãn. Các hệ số Fourier là x[n], ta có thể tính được x[n] từ X( ) theo cách sau:
Nhân 2 vế của biểu thức DTFT với
1 e jl
2
rồi lấy tích phân trong khoảng
( ,) tacó
1 1
1
X ()e jl d
x[n]ejn e jl dx[n]
e j(l n) dx[l]
2
2n
n
2
(1.15)
Thay l = n và thay cận tích phân, không nhất thiết phải là ( ,) mà chỉ cần khoảng giữa cân trên và dưới là 2 , ta được biểu thức tính biến đổi Fourier ngược (IDTFT) như sau:
x[n] 1X ()e jn d
22
(1.16)
Ta có thể tính IDFT bằng hai cách : một là tính trực tiếp tích phân trên, hai là chuyển về biến đổi Z rồi tính như biến đổi Z ngược. Tuỳ vào từng trường hợp cụ thể mà ta chọn phương pháp nào cho thuận tiện.
1.6.4 Các tính chất của phép biến đổi Fourier
Tính tuyến tính Tính dịch thời gian
ax1[n] bx2[n] aX1 () bX2 ()
xnX
(1.17)
xn n0 e 0 X
jn
(1.18)
Qua đây ta thấy sự dịch chuyển tín hiệu trong miền thời gian sẽ không ảnh hưởng biên độ của DTFT, tuy nhiên pha được thêm một lượng.
Tính dịch tần số / điều chế
x[n] X ()
0
e j0n x[n] X ( )
(1.18)
cos(n)x[n] 1 x( ) 1 X ( )
0 2 0 2 0
Như vây, việc điều chế gây ra dịch tần số.
Tính chập thời gian
Tương tự như biến đổi Z, với biến đổi Fourier ta cũng có:
x [n]* x [n]FX
() X
()
(1.19)
1
Tính nhân thời gian
2 1 2
x [n].x [n] 1 X () X
()d
(1.20)
2
1 2 1 2
2
1.6.5 Phân tích tần số (phổ) cho tín hiệu rời rạc
Trong miền tần số, mỗi tín hiệu đều có một đặc điểm riêng của nó. Ví dụ như, tín hiệu sin chỉ có duy nhất một tần số đơn, trong khi nhiễu trắng chứa tất cả các thành phần tần số. Sự biến thiên chậm của tín hiệu là do tần số thấp, trong khi sự biến thiến
nhanh và những xung nhọn là do tần số cao. Như xung vuông chẳng hạn, nó chứa tất cả tần số và cả tần số cao.
Phổ của tín hiệu là mô tả chi tiết các thành phần tần số chứa bên trong tín hiệu. Ví dụ như tín hiệu xung vuông, phổ của nó chỉ ra tất cả các đỉnh nhọn của các sóng sin riêng có thể kết hợp lại hợp với nhau tạo ra xung vuông. Thông tin này quan trọng vì nhiều lý do. Ví dụ, thành phần tần số trong một mẫu nhạc chỉ cho ta biết các đặc trưng của loa, để từ đó khi sản xuất ta lại có cải tiến cho hay hơn. Để dự đoán các ảnh hưởng của bộ lọc trên tín hiệu, cần phải biết không chỉ bản chất của bộ lọc mà còn phải biết cả phổ của tín hiệu nữa.
1.6.6 Phổ tín hiệu và phổ pha
Phổ của tín hiệu gồm hai phần: phổ biên độ (magnitude spectrum) và phổ pha (phase spectrum). Phổ biên độ chỉ ra độ lớn của từng thành phần tần số. Phổ pha chỉ quan hệ pha giữa các thành phần tần số khác nhau. Công cụ để tính phổ tín hiệu rời rạc không tuần hoàn là DTFT.
Để tính phổ tín hiệu , ta qua hai bước : một là tính DTFT của tín hiệu – là X( ), hai là tính biên độ và pha của X( ):
X ()
X () e j()
(1.21)
ở đây |X( )| là phổ biên độ và ( ) là phổ pha.
Ta dễ dàng chứng minh được rằng đối với tín hiệu thực, phổ biên độ là một hàm chẵn theo tần số và phổ pha là một hàm lẻ theo .
Do đó, nếu biết phổ X( ) trong khoảng 0 đến , ta có thể suy ra phổ trong toàn dải tần số. Để dễ giải thích phổ, tần số số từ 0 đến thường được chuyển đổi thành tần số tương tự từ 0 đến fs/2 nếu tần số lấy mẫu là fs.
1.7 CÁC THUẬT TOÁN SỬ DỤNG NÂNG CAO CHẤT LƯỢNG TIẾNG NÓI
1.7.1 Trừ phổ
Spectral-subtraction (SS) hay còn gọi là trừ phổ là một thuật toán giảm nhiễu đơn giản nhất. Nó dựa trên nguyên lý cơ bản là nó sẽ mô tả và cập nhật nhiễu trong tín hiệu có nhiễu bằng cách thu nhiễu khi không có sự hiện diện của tín hiệu. Và nhiễu đó sẽ được trừ với tín hiệu có nhiễu, kết quả là tín hiệu của chúng ta sau khi xử lý bằng thuật toán này sẽ được loại đi nhiễu và xét trên phương diện lý tưởng thì nó là tín hiệu sạch. SS lúc ban đầu được đề xuất bởi Weiss trong miền tương quan, và sau đó được đề xuất bởi Boll trong miền chuyển đổi Fourier.
1.7.2 Mô hình thống kê
Vấn đề của nâng cao chất lượng tiếng nói là phải đề ra được khung mô tả mang tính thống kê. Nó là một tập các phép đo tương ứng với hệ chuyển đổi Fourier của tín hiệu nhiễu, và chúng ta mong muốn sẽ tìm ra được một phương thức ước lượng tuyến tính hoặc phi tuyến các tham số có lợi, đó là hệ chuyển đổi của tín hiệu sạch. Hai thuật toán được sử dụng đó là thuật toán Wiener và minium mean-squared error(MMSE).
1.8 TÍN HIỆU TIẾNG NÓI
Tín hiệu tiếng nói là tín hiệu liên tục và có phổ năng lượng thay đổi theo thời gian. Tuy nhiên khi khảo sát trong một khoảng thời gian đủ ngắn (khoảng 10 đến 30 ms) thì đặc tính phổ của nó coi như không thay đổi.
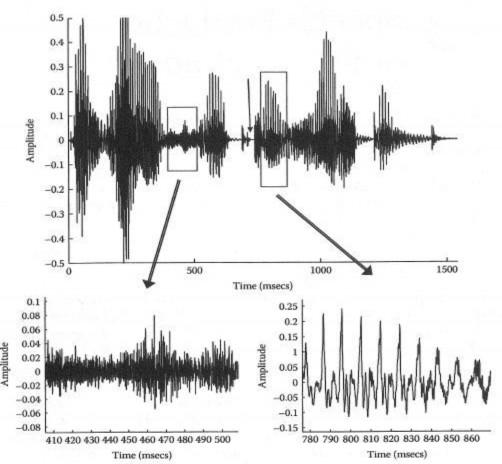
Hình 1.6 Dạng sóng tín hiệu tiếng nói của câu “The wife helped her husband” và dạng sóng của phụ âm “f” trong từ “wife, dạng sóng của đoạn nguyên âm “er”
trong từ “her”.
Dạng sóng của tín hiệu có thể được chia thành một số phân đoạn tương ứng với các âm/từ. Trong ví dụ trên ta thấy một số phân đoạn có dạng sóng gần như tuần hoàn còn số khác thì không có tính tuần hoàn và bị nhiễu.
Những kiểu của đoạn tiếng nói_chu kỳ, nhiễu, khoảng lặng… thường được tìm thấy trong tiếng nói trôi chảy với sự thay đổi về cường độ, khoảng thời gian và đặc tính phổ.
1.9 CƠ CHẾ TẠO TIẾNG NÓI
1.9.1 Bộ máy phát âm của con người
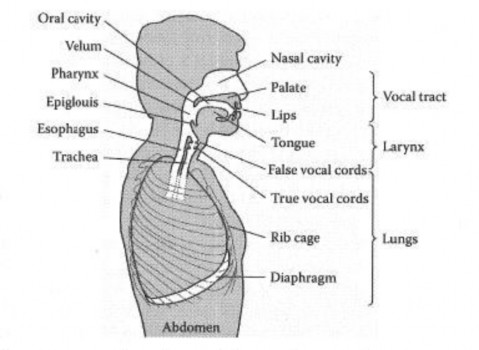
Hình 1.7 Mặt cắt dọc của cơ quan tạo tiếng nói.
1.9.2 Mô hình kỹ thuật của việc tạo tiếng nói
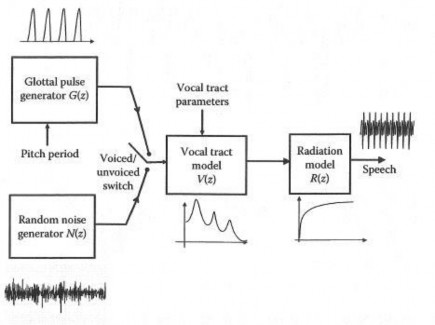
Hình 1.8 Mô hình kỹ thuật tạo tiếng nói.
1.9.3 Phân loại âm
Các âm trong tiếng Anh được phân loại gồm: nguyên âm và nguyên âm đôi, bán nguyên âm, âm mũi, âm stops, fricative, africatives, whisper.
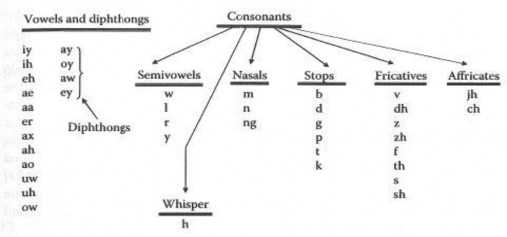
Hình 1.9 Bảng phân loại âm vị trong tiếng Anh của người Mỹ.
1.9.4 Thuộc tính âm học của tiếng nói
Tín hiệu tiếng nói là tín hiệu tương tự, biểu diễn cho thông tin về mặt ngôn ngữ và được thể hiện bằng các âm vị khác nhau. Số lượng các âm vị tuỳ thuộc vào từng ngôn ngữ, vào khoảng 20 đến 30 và không vượt quá 50. Đối với từng loại âm vị nó có đặc tính âm thanh khác nhau.Tổ hợp các âm vị tạo nên âm tiết. Âm tiết đóng vai trò một từ trọn vẹn mang ngữ nghĩa.
1.10 KẾT LUẬN CHƯƠNG
Chương này đã trình bày được mục đích chính của speech enhancement là triệt nhiễu hoặc là nén nhiễu trong tín hiệu tiếng nói đã bị nhiễu. Ngoài ra, nội dung của chương cũng đã nêu rõ được các loại nhiễu xuất hiện trong từng môi trường cụ thể để từ đó chúng ta có tìm ra được thuật toán xử lý thích hợp ứng với mỗi trường hợp cụ thể.