(A) Định lý cho P1&P2:
(a) P1&P2 ≡ P1 nếu P1 = (A, (b) P1&P2 ≡ P1 + (A1↔&P2) nếu A1 ∩ A2 = □ Chứng minh: (a) Cho P1 = (A, ∧ x (b) Cho P1 = (A1, = (y1, y2) ∈ dom(A1) × dom(A2) cho x thứ tự được nhúng vào P1* = (A1 ∪ A2, Có thể bạn quan tâm! Xem toàn bộ 83 trang tài liệu này. Do đó P1* + (A1↔ &P2) = (A1 ∪ A2, không giao nhau. Chúng ta có: x nếu x Định lý “Non-discrimination”: P1 □ P2 ≡ (P1 & P2) ♦ (P2 & P1) Chứng minh: Cho P1 = (A1, Khi đó: P1 □ P2 = (A1 ∪ A2, P1 = (A2 ∪ A1, <(P1&P2)♦(P2&P1)) Cho x = (x1, x2) and y = (y1, y2) ∈ dom(A1) × dom(A2). Rút gọn: B := ‘x1 y, sau đó ¬B ∧ ¬D được thực hiện. Các trường hợp khác, nếu x ≠ y, sau đó ¬C ∨ ¬D thực hiện. (*) (1) x nếu (B ∧ E) ∨ (B ∧ D) ∨ (D ∧ C) (2) x <(P1&P2)♦(P2&P1) y nếu (B ∨ (C ∧ D)) ∧ (D ∨ (E ∧ B)) nếu (B ∧ (D ∨ (E ∧ B))) ∨ ((C ∧ D) ∧ (D∨ (E ∧ B))) nếu (B ∧ D) ∨ (B ∧ E ∧B) ∨ (C ∧ D ∧ D) ∨ ((C ∧ E) ∧D ∧ B) nếu x (**) Hãy chú ý vào H := C ∧ E ∧ D ∧ B trong (**) bên trên: Trong cả hai trường hợp x ≠ y hoặc x = y, dẫn đến (*) ¬H bị ảnh hưởng. Do đó, ngay lập tức từ đại số Boolean, chúng ta có thể tiếp tục (**): khi và chỉ khi x (C) Định lý: σ[P1+P2](R) = σ[P1](R) ∩ σ[P2](R) Chứng minh: Nghiên cứu P1+P2 = (A, ∈ R[A]: w ∈ Nmax((P1+P2)R) khi và chỉ khi □ v ∈ R[A]: w và chỉ khi □ v ∈ R[A]: w khi và chỉ khi (□ v ∈ R[A]: w khi và chỉ khi w ∈ Nmax(P1R) ∨ w ∈ Nmax(P2R) Do đó: Nmax((P1+P2)R) = Nmax(P1R) ∪ Nmax(P2R) thì: σ[P1+P2](R) = {t ∈ R: t[A] ∈ max((P1+P2)R)} = {t ∈ R: t[A] ∈ R[A] − Nmax((P1+P2)R)} = {t ∈ R: t[A] ∈ R[A] − (Nmax(P1R) ∪ Nmax(P2R))} = {t ∈ R: t[A] ∈ (R[A] − Nmax(P1R)) ∩ (R[A] − Nmax(P2R))} = {t ∈ R: t[A] ∈ max(P1R) ∩ max(P2R)} = σ[P1](R) ∩ σ[P2](R) (D) Định lý: σ[P1♦P2](R) = σ[P1](R) ∪ σ[P2](R) ∪ YY(P1, P2)R Chứng minh: Nghiên cứu P1♦P2 = (A, Khi và chỉ khi □ v ∈ R[A]: w Khi và chỉ khi □ v ∈ R[A]: w nếu □ v, v’ ∈ R[A]: w (v ∈ P1↑w ∧ v’ ∈ P2↑w ∧ v = v’) nếu (□ v ∈ R[A]: w Nmax(P1R), □ v’ ∈ Nmax(P2R): v ∈ P1↑w ∧ v’ ∈ P2↑w ∧ v = v’) nếu w ∈ Nmax(P1R) ∧ w ∈ Nmax(P2R) ∧ (□ v ∈ Nmax(P1R), □ v’ ∈ Nmax(P2R): v ∈ P1↑w ∧ v’ ∈ P2↑w ∧ v = v’) dẫn đến XX(P1, P2)R := {w ∈ R[A]: □ v ∈ Nmax(P1R), □ v’∈ Nmax(P2R): v ∈ P1↑w ∧ v’ ∈ P2↑w ∧ v = v’} chúng ta có: nếu w ∈ Nmax(P1R) ∧ w ∈ Nmax(P2R) ∧ w ∈ XX(P1, P2)R do đó: Nmax((P1♦P2)R) = Nmax(P1R) ∩ Nmax(P2R) ∩ XX(P1, P2)R sau đó chúng ta có: σ[P1♦P2](R) = {t ∈ R: t[A] ∈ max((P1♦P2)R)} = {t ∈ R: t[A] ∈ R[A] − Nmax((P1♦P2)R)} = {t ∈ R: t[A] ∈ R[A] − (Nmax(P1R) ∩ Nmax(P2R) ∩ XX(P1, P2)R)} = {t ∈ R: t[A] ∈ (R[A] − Nmax(P1R)) ∪ (R[A] − Nmax(P2R)) ∪ (R[A] − XX(P1, P2)R)} = {t ∈ R: t[A] ∈ max(P1R) ∪ max(P2R) ∪ (R[A] − XX(P1, P2)R)} = σ[P1](R) ∪ σ[P2](R) ∪ {t ∈ R: t[A] ∈ R[A] − XX(P1, P2)R} Chúng ta có: t[A] ∈ R[A] − XX(P1, P2)R nếu t[A] □ XX(P1, P2)R nếu t[A] ∈ {w ∈ R[A]: ¬(□ v ∈ Nmax(P1R), □ v’ ∈ Nmax(P2R): v ∈ P1↑w ∧ v’ ∈ P2↑w ∧ v = v’) nếu ¬(□ v ∈ Nmax(P1R), □ v’ ∈ Nmax(P2R): v ∈ P1↑t[A] ∧ v’ ∈ P2↑t[A] ∧ v = v’) nếu ¬( t[A] ∈ Nmax(P1R) ∩ Nmax(P2R): P1↑t[A] ∩ P2↑t[A] ≠ □) nếu (t[A] ∈ Nmax(P1R) ∩ Nmax(P2R): P1↑t[A] ∩ P2↑t[A] = □) dẫn đến YY(P1, P2)R := {t ∈ R : t[A] ∈ Nmax(P1R) ∩ Nmax(P2R) ∧ P1↑t[A] ∩ P2↑t[A] = □} kết quả là: σ[P1♦P2](R) = σ[P1](R) ∪ σ[P2](R) ∪YY(P1, P2)R.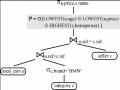 Thiết Kế Ngôn Ngữ Sql Hướng Người Dùng.
Thiết Kế Ngôn Ngữ Sql Hướng Người Dùng. Môi Trường Thực Thi Của Sql Ưa Thích.
Môi Trường Thực Thi Của Sql Ưa Thích.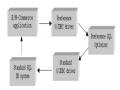 Truy vấn dữ liệu hướng người dùng - 9
Truy vấn dữ liệu hướng người dùng - 9
