Nhập môn trí tuệ nhân tạo - 26

Ví dụ 5.31 : Hàm tính tổng plus(X, Y, Z):-

nonvar(X), nonvar(Y), Z is X + Y.

plus(X, Y, Z):- nonvar(Y), nonvar(Z), X is Z - Y.

plus(X, Y, Z):- nonvar(X), nonvar(Z), Y is Z - X.

Ví dụ 5.32: Thuật toán hợp nhất

Sau đây là một thuật toán hợp nhất đơn giản cho phép xử lý trường hợp một

biến nào đó được thay thế (hợp nhất) bởi một hạng mà hạng này lại có chứa đúng tên biến đó. Chẳng hạn phép hợp nhất X = f(X) là không hợp lệ.

% unify(T1, T2).

unify(X, Y):- % trường hợp 2 biến var(X), var(Y), X = Y.

unify(X, Y):- % trường hợp biến = không phải biến var(X), nonvar(Y), X = Y.

unify(X, Y):- % trường hợp không phải biến = biến nonvar(X), var(Y), Y = X.

unify(X, Y):- % nguyên tử hay số = nguyên tử hay số nonvar(X), nonvar(Y),

atomic(X), atomic(Y), X = Y.

unify(X, Y):- % trường hợp cấu trúc = cấu trúc nonvar(X), nonvar(Y),

compound(X), compound(Y), termUnify(X, Y).

termUnify(X, Y):- % hợp nhất hạng với hạng chứa cấu trúc functor(X, F, N),

functor(Y, F, N),

argUnify(N, X, Y).

argUnify(N, X, Y):- % hợp nhất N tham đối của X và Y N>0,

argUnify1(N, X, Y), Ns is N - 1, argUnify(Ns, X, Y). argUnify(0, X, Y).

argUnify1(N, X, Y):- % hợp nhất các tham đối có bậc N arg(N, X, ArgX),

arg(N, Y, ArgY), unify(ArgX, ArgY).

CÂU HỎI VÀ BÀI TẬP CHƯƠNG 5

5.1. Trình bày thủ tục lập luận tiến.

5.2. Trình bày thủ tục lập luận lùi.

5.3. Cho CSTT được biểu diễn bằng các biểu thức logic sau:

7) QT  S

8) APQ  C

9) PQ  B

10) BC  T

11) PA

12) PQ

Biểu diễn tri thức đã cho dưới dạng luật nếu thì và dùng phương pháp lập luận tiến và lập luận lùi để chứng minh S.

5.4. Cho CSTT được biểu diễn bằng các biểu thức logic sau: 6) (AC) B  F

7) E FA

8) GF  I

9) (E F) B  G

10)BC

Dùng phương pháp lập luận tiến và lập luận lùi để chứng minh I.

5.5. Cho CSTT được biểu diễn bằng các biểu thức logic sau:

1) EFH

2) AGD

3) HCD

4) AF  BG

5) KE  D

6) (EF  A)(CE F)

Dùng phương pháp lập luận tiến để chứng minh D.

5.6. Trong một lớp học, có một nhóm học sinh gồm 10 bạn có tên lần lượt là: A, B, C, D, E, F, G, H, I và J. Giữa các bạn học sinh đó có mối quan hệ gọi là quan hệ ảnh hưởng. Ví dụ: nếu ta viết AB>C thì có nghĩa là hai bạn đồng thời cùng thuyết phục bạn C tham gia một hoạt động nào đó. Giả sử ban đầu có bốn bạn E, F, H, I tham gia dự thi sản phẩm phần mềm do nhà trưòng tổ chức và ta cũng biết được rằng:

1) ACH>B

2) BH>ACD

3) ABCI>BDI

4) ADEI>BCG

5) CGI>AJE

6) H>BC

Hãy dùng phương pháp lập luận để chứng minh rằng cả 10 bạn trong nhóm trên đều tham gia dự thi sản phẩm phần mềm.

5.7. Cho CSTT mô tả mối quan hệ giữa các cạnh, góc, đường cao, chu vi, diện tích tam giá như sau:

a  b  c  p b  p  c  a a  p  c  b a  b  p  c S  c  hc

a  b  C  c a  b  C  S

a  b  c  p  S S  hc  c

(Trong đó: a, b, c là ký hiệu các cạnh, A, B, C là ký hiệu các góc tương ứng, p là ký hiệu nữa chu vi, và hc là đường cao xuất phát từ đỉnh C của tam giác)

Giả sử ta biết các cạnh a, b và một góc C. Ta có thể tính được đường cao hc không?

HƯỚNG DẪN GIẢI BÀI TẬP

1. Bài tập Chương 2 Bài 2.7.

-Xây dựng không gian trạng thái của bài toán

Để biểu diễn các trạng thái, ta sử dụng bộ ba (a, b, k), trong đó a là số triệu phú, b là số kẻ cướp ở bên bờ tả ngạn vào các thời điểm mà thuyền ở bờ này hoặc bờ kia, k = 1 nếu thuyền ở bờ tả ngạn và k = 0 nếu thuyền ở bờ hữu ngạn.

+ Trạng thái ban đầu là (2, 2, 1).

+ Trạng thái kết thúc là (0, 0, 0).

+ Có 5 toán tử tương ứng với hành động thuyền chở qua

sông 1 triệu phú, hoặc 1 kẻ cướp, hoặc 2 triệu phú, hoặc 2 kẻ cướp, hoặc 1 triệu phú và 1 kẻ cướp.

- Tìm một lời giải b1. (2, 2, 1)

b2. (2, 0, 0)

b3. (2, 1, 1)

b4. (0, 1, 0)

b5. (1, 1, 1)

b6. (0, 0, 0)

Bài 2.8.

-Xây dựng không gian trạng thái của bài toán

Để biểu diễn các trạng thái, ta sử dụng bộ (a, b), trong đó a là lượng nước của bình A, b là lượng nước của bình B tại thời điểm đang xét

+ Trạng thái ban đầu là (0, 0)

+ Tập trạng thái kết thúc là

T={(1, y), 0≤y≤7}  {(x, 1), 0≤x≤4}

+ Các toán tử:

(a, b)  (0, b) (a>0)

(a, b)  (a, 0) (b>0)

(a, b)  (4, b) (a<4)

(a, b)  (a, 7) (b<7)

(a, b)  (a+b, 0) (a+b3)

(a, b)  (0, a+b) (a+b7)

(a, b)  (4, a+b-4) (a<4, a+b>4)

(a, b)  (a+b-7, 7) (b<7, a+b>7)

-Tìm một lời giải b1. (0, 0)

b2. (4, 0)

b3. (0, 4)

b4. (4, 4)

b5. (1, 7)

Bài 2.9.

-Xây dựng không gian trạng thái của bài toán

- Để biểu diễn các trạng thái, ta sử dụng bộ (a, b), trong đó a là lượng nước của bình A, b là lượng nước của bình B tại thời điểm đang xét.

Hướng dẫn giải

+ Trạng thái ban đầu là (0, 0)

+ Tập trạng thái kết thúc là: T={(x, 8), 0≤x≤3}

+ Các toán tử:

(a, b)  (0, b) (a>0)

(a, b)  (a, 0) (b>0)

(a, b)  (3, b) (a<3)

(a, b)  (a, 8) (b<8)

(a, b)  (a+b, 0) (a+b3)

(a, b)  (0, a+b) (a+b8)

(a, b)  (3, a+b-3) (a<3, a+b>3)

(a, b)  (a+b-8, 8) (b<8, a+b>8)

-Tìm một lời giải b1. (0, 0)

b2. (0, 8)

b3. (3, 5)

b4. (0, 5)

b5. (3, 2)

b6. (0, 2)

b7. (2, 0)

b8. (2, 8)

b9. (3, 7)

Bài 2.10.

Hướng dẫn giải

Khởi tạo:

uo=A, T={G} d=2

u

Kề u	l	Father (F)
		A(12, 0)
A(12, 0)	B(5, 1), C(7, 1), K(8, 1)	K(8, 1), C(7, 1), B(5, 1)	F(C) =A F(B) =A F(K) =A
K(8, 1)	H(4, 2), C(7, 2)	C(7, 2), H(4, 2), C(7, 1), B(5, 1)	F(H) =K F(C) =K
C(7, 2)	E(3, 3), D(4, 3)	D(4, 3), E(3, 3), H(4, 2), C(7, 1), B(5, 1)	F(E) =C F(D) =C
D(4, 3) loại
E(3, 3) loại
H(4, 2)	E(3, 3)	E(3, 3), C(7, 1), B(5, 1)	F(E) =H
E(3, 3) loại		C(7, 1), B(5, 1)
C(7, 1)	D(4, 2), E(3, 2)	D(4, 2), E(3, 2), B(5, 1)	F(D) =C F(E) =C
D(4, 2)	G(0, 3)	G(0, 3), E(3, 2), B(5, 1)	F(G) =D
G(0, 3)  T	Tìm kiếm thành công
Kết luận: đường đi GDCKA

Có thể bạn quan tâm!

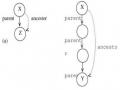
• Các Cặp Tổ Tiên Hậu Duệ Gián Tiếp Ở Các Mức Khác Nhau
• Mô Hình Vào/ra Của Một Thủ Tục Thực Hiện Một Danh Sách Các Đích
• Nhập môn trí tuệ nhân tạo - 25
• Nhập môn trí tuệ nhân tạo - 27
• Nhập môn trí tuệ nhân tạo - 28
• Nhập môn trí tuệ nhân tạo - 29

Xem toàn bộ 272 trang tài liệu này.

Bài 2.11.

Khởi tạo:

uo=A, T={G}; d=2

U

Kề u	l	Father (F)
		A(17, 0)
A(17, 0)	C(8, 1) G(5, 1) K(4, 1)	C(8, 1), G(5, 1) K(4, 1)	F(C) =A F(G) =A F(K) =A
C(8, 1)	D(6, 2)	D(6, 2), G(5, 2)	F(D) =C

Kề u	l	Father (F)
	G(5, 2)	G(5, 1), K(4, 1)	F(G) =C
D(6, 2)	E(5, 3) H(4, 3)	E(5, 3), H(4, 3), G(5, 2), G(5, 1), K(4, 1)	F(E) =D F(H) =D
E(5, 3)	loại	H(4, 3), G(5, 2), G(5, 1), K(4, 1)
H(4, 3)	loại	G(5, 2), G(5, 1), K(4, 1)
G(5, 2)	K(4, 3), H(4, 3), D(6, 3)	D(6, 3), K(4, 3), H(4, 3), G(5, 1), K(4, 1)	F(K) =G F(H) =G
D(6, 3)	loại	K(4, 3), H(4, 3), G(5, 1), K(4, 1)
K(4, 3)	loại	H(4, 3), G(5, 1), K(4, 1)
H(4, 3)	loại	G(5, 1), K(4, 1)	F(D) =C F(E) =C
G(5, 1)	D(6, 2), H(4, 2), K(4, 2)	D(6, 2), K(4, 2), H(4, 2), K(4, 1)	F(D) =G F(H) =G F(K) =G
D(6, 2)	E(5, 3), H(4, 3)	E(5, 3), H(4, 3), H(4, 2), K(4, 2), K(4, 1)	F(E) =D F(H) =D
E(5, 3)	loại	H(4, 3), H(4, 2), K(4, 2), K(4, 1)
H(4, 3)	loại	H(4, 2), K(4, 2), K(4, 1)
H(4, 2)	F(0, 3), B(6, 3)	B(6, 3), F(0, 3), K(4, 2), K(4, 1)	F(F) =H F(B) =H
B(6, 3)	loại	F(0, 3), K(4, 2), K(4, 1)
F(0, 3)  T	dừng
Kết luận: tìm thấy đường đi FHDGCA

U

Bài 2.12.

1. Sử dụng thuật toán leo đồi để tìm đường đi từ đỉnh uo=A đến đỉnh B. Khởi tạo:

uo=A, T={B}

u

Kề u	l1	L	Father (F)
			A(12)
A(12)	C(7), D(6), K(4)	K(4), D(6),	K(4), D(6), C(7)	F(D) =A