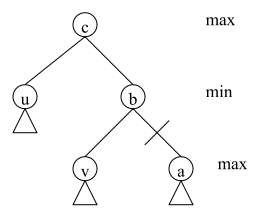
Hình 2.38. Cắt bỏ cây con gốc a nếu eval(u)>eval(v)
Khi đó ta có giá trị đỉnh Trắng c ít nhất là giá trị của u, giá trị của đỉnh Đen b nhiều nhất là giá trị của v. Do đó, nếu eval(u) > eval(v) ta không cần đi xuống để đánh giá đỉnh a nữa mà vẫn không ảnh hưởng đến đánh giá đỉnh c. Hay nói cách khác, ta có thể cắt bỏ cây con gốc a.
Lập luận tương tự cho trường hợp a là đỉnh Đen, trường hợp này nếu val(u)<eval(v) ta cũng cắt bỏ cây con gốc a.
Để cài đặt kỹ thuật này, đối với các đỉnh nằm trên đường đi từ gốc tới đỉnh hiện thời, ta sử dụng tham số α để ghi lại giá trị lớn nhất trong các giá trị của các đỉnh con đã đánh giá của một đỉnh Trắng, tham số β để ghi lại giá trị nhỏ nhất trong các giá trị của các đỉnh con đã đánh giá của một đỉnh Đen.
Thuật toán:
Procedure Alpha_Beta(u, v); begin
α←-∞; β←-∞;
for mỗi w là đỉnh con của u do if α <= MinVal(w, α, β) then
{α ← MinVal(w, α, β); v ← w} end;
Có thể bạn quan tâm!
-
Một Phần Đồ Thị Không Gian Trạng Thái Của Ví Dụ 2.22 -
Đồ Thị Không Gian Trạng Thái Với Hàm Đánh Giá -
Các Giải Thuật Tìm Kiếm Lời Giải Cho Trò Chơi -
Cú Pháp Và Ngữ Nghĩa Của Logic Mệnh Đề -
Các Quy Tắc Xây Dựng Các Công Thức -
Luật Phân Giải. Thủ Tục Chứng Minh Bác Bỏ Bằng Luật Phân Giải
Xem toàn bộ 272 trang tài liệu này.
---------------------------------------------------
Function MinVal(u, α, β); {hàm xác định giá trị cho các đỉnh Đen} begin
if u là đỉnh kết thúc or u là lá của cây hạn chế then MinVal(u, α, β) ← eval(u)
else for mỗi đỉnh v là con của u do Begin
β ← min{β, MaxVal(v, α, β) ; If α >= β then exit;
End;
/*cắt bỏ các cây con từ các đỉnh v còn lại */ MinVal(u, α, β) ← β;
end;
---------------------------------------------------
Function MaxVal(u, α, β); { hàm xác định giá trị cho các đỉnh Trắng} begin
if u là đỉnh kết thúc or là lá của cây hạn chế then MaxVal(u, α, β) ← eval(u)
Else
for mỗi đỉnh v là con của u do Begin
α ← max{α, MinVal(v, α, β)} ; If α >= β then exit;
End;
/*cắt bỏ các cây con từ các đỉnh v còn lại */ MaxVal(u, α, β) ← α
end;
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 2
2.1. Trình bày khái niệm không gian trạng thái và biểu diễn vấn đề trong KGTT. Cho ví dụ minh họa.
2.2. Trình bày các chiến lược tìm kiếm mù: tìm kiếm theo chiều sâu, chiều rộng, sâu lặp.
2.3. Trình bày các chiến lược tìm kiếm trên đồ thị và/ hoặc.
2.4. Trình bày các chiến lược tìm kiếm kinh nghiệm: tìm kiếm tốt nhất- đầu tiên, leo đồi. Cho ví dụ minh họa.
2.5.Trình bày các chiến lược tìm kiếm A*. 2.6.Trình bày các chiến lược tìm kiếm nhánh cận.
2.7. Có một chiếc thuyền trên bờ tả ngạn một con sông. Mỗi lượt, thuyền chỉ chở được tối đa 2 người. Hãy tìm cách để chở 2 kẻ cướp và 2 nhà buôn đi thuyền từ tả ngạn sang hữu ngạn sông sao cho ở mỗi bờ sông, số nhà buôn ở mọi thời điểm luôn không nhỏ hơn số kẻ cướp (trừ trường hợp bên một bờ sông không có nhà buôn nào). Nhà buôn và kẻ cướp có thể qua lại hai bên bờ sông nhiều lần.
Miêu tả không gian trạng thái của bài toán và tìm một lời giải cho bài toán.
2.8. Cho 2 bình A và B lần lượt có dung tích 4 lít và 7 lít và không có vạch chia độ. Ban đầu 2 bình không có nước. Có thể rót nước đổ đầy các bình, có thể đổ hết nước từ một bình đi, có thể rót nước từ bình này sang bình khác. Hãy xây dựng không gian trạng thái của bài toán để rót được đúng 1 lít nước và hãy chỉ ra 1 cách rót.
2.9. Cho 2 bình A, B lần lượt có dung tích 3 lít và 8 lít và không có vạch chia độ. Ban đầu 2 bình không có nước. Có thể rót nước đổ đầy các bình, có thể đổ hết nước từ một bình đi, có thể rót nước từ bình này sang bình khác.
Hãy xây dựng không gian trạng thái của bài toán để rót được đúng 7 lít nước và hãy chỉ ra 1 cách rót.
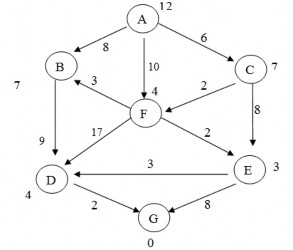
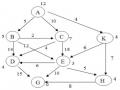
2.10. Hãy sử dụng thuật toán tìm kiếm sâu lặp để tìm đường đi từ A tới G với độ sâu d=3 theo thứ tự tăng dần của trọng số các đỉnh trong đồ thị trạng thái. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
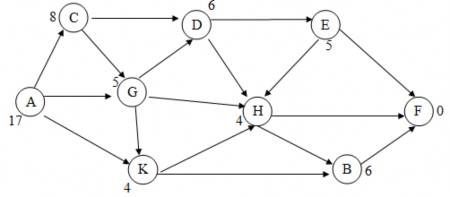
2.11. Cho đồ thị trạng thái trong hình bên dưới. Hãy sử dụng thuật toán sâu lặp để tìm đường đi từ đỉnh uo=A đến đỉnh F với độ sâu d=3 theo thứ tự tăng dần của trọng số các đỉnh. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
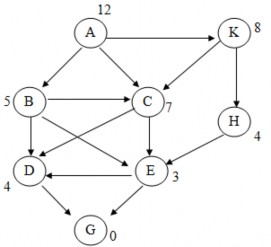
2.12. Cho đồ thị trạng thái
1. Sử dụng thuật toán leo đồi để tìm đường đi từ đỉnh uo=A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
2. Sử dụng thuật toán sâu lặp để tìm đường đi từ A đến B với độ sâu d=1 theo thứ tự tăng dần của trọng số các đỉnh. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
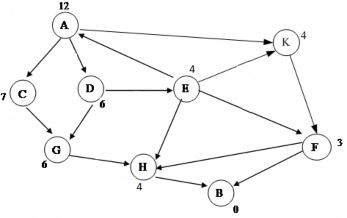
2.13. Cho đồ thị trạng thái.
1. Hãy sử dụng thuật toán tốt nhất-đầu tiên để tìm đường đi từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
2. hãy sử dụng thuật toán sâu lặp để tìm đường đi từ A đến G với độ sâu d=1 theo thứ tự tăng dần của trọng số các đỉnh. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
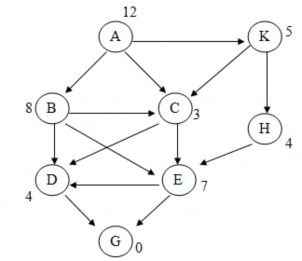
2.14. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* tìm đường đi ngắn nhất từ đỉnh u0 = A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
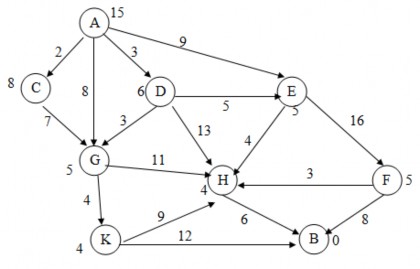
2.15. Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận tìm đường đi ngắn nhất từ đỉnh u0 = A đến đỉnh F. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
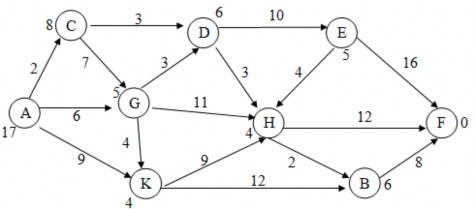
2.16 Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận tìm đường đi ngắn nhất từ đỉnh u0 = A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
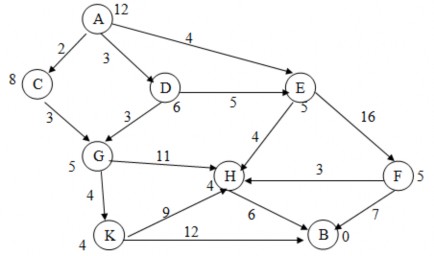
2.17. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* tìm đường đi ngắn nhất từ đỉnh u0 = A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
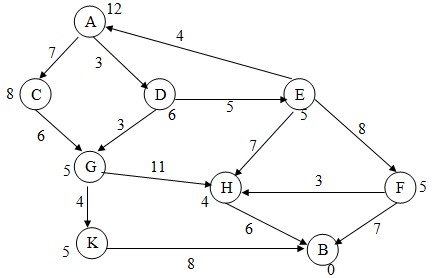
2.18. Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận tìm đường đi ngắn nhất từ đỉnh u0 = A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
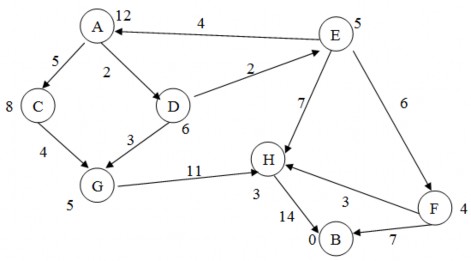
2.19. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
12
A
10
K 4
4
7
5
C
D
6
6
5
E
4
7
6
6
9
G
14
3
F
6
H
7
4
6
B
0
7
7
3
2.20. Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
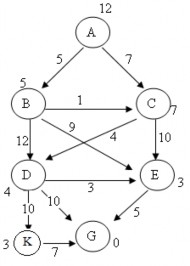
2.21. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
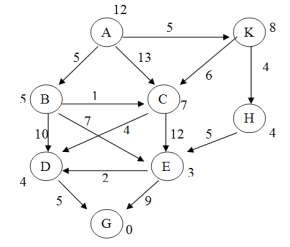
2.22. Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.
