Đánh Giá Độ Phức Tạp Và Cài Đặt Thuật Toán

T3,1

1 2 3

T6,1

1 2 3 4 5 6

T3,2

1 2 5

Có thể bạn quan tâm!

Xem toàn bộ 136 trang tài liệu này.

Ta có:

- T2,1 = T1,1  T1,2;

- T3,3= T2,4  T1,2 = T2,5  T1,2

T5,1 = T4,1  T1,5 = T4,2  T1,4 = T3,2  T2,4= T4,4  T1,1

3.4.4. Nguyên lý tối ưu hóa

Phần này sẽ chỉ ra rằng bài toán tối ưu hóa truy vấn cây phân tán tuân thủ nguyên lí tối ưu hóa [34]. Giả thiết rằng một truy vấn i-lớp Ti,j là một truy vấn con của truy vấn cây T với n lớp và nó được chia thành một truy vấn con r-lớp Tr,pvà truy vấn con (i-r)-lớp Ti-r,q. Trong số tất cả các kế hoạch có thể thực hiện để đưa kết quả kết quả của Tr,p ở trạm x, giả sử có một kế hoạch au(x).Trong số tất cả các kế hoạch có thể thực hiện để đưa kết quả kết quả của Ti-r,q ở trạm x, giả sử có một kế hoạch bv(x). Gọi Cost(p) là chi phí của kế hoạch p. Các kế hoạch thực thi cho phép kết nối ẩn và phép truyền được tạo ra bởi các hàm sau đây.

- Hàm buildJPlanx(au(x), bv(x)) kết hợp kế hoạch au(x) và bv(x) vào một kế hoạch trong đó các kết quả của Tr,p và Ti-r,q ở trạm x được nối ẩn ở trạm này, đó là buildJPlanx(au(x), bv(x)) = IJx(au(x), bv(x)). Kí hiệu cw(x) là kế hoạch được tạo ra bởi hàm trên. Bằng cách thực hiện kế hoạch này, kết quả của Ti,j được tính tường minh ở trạm x.

- Hàm buildTPlanx,t(cw(x)) mở rộng kế hoạch vào kế hoạch khác trong đó kết quả của Ti,j ở trạm x được truyền tới trạm t, buildTPlanxt(cw(x)) =TR x,t(cw(x)). Thực hiện kế hoạch này sẽ lấy được kết quả của Ti,j ở trạm t.

Vì kết quả của Tr,p và Ti-r,q phải ở cùng trạm để được nối ẩn, chi phí của kế hoạch được tạo ra bởi buildJPlanx(au(x), bv(x)) là tổng của các chi phí để lấy kết quả của các truy vấn Tr,pvà Ti-r,q ở trạm x và chi phí cho nối ẩn ở trạm này. Tương tự, chi phí của kế hoạch được tạo ra bởi buildTPlanx,t(cw(x)) là tổng kết quả chi phí đã

tính tường minh cho truy vấn ở trạm x và chi phí truyền kết quả của truy vấn Ti,j từ trạm x về trạm t. Do vậy, chúng ta có:

Cost(buildJPlanx(au(x), bv(x)))=Cost(au(x))+Cost(bv(x))+joinx(Tr,p,Ti-r,q ) (3.6) Cost(buildTPlan x,t(cw(x))) = Cost(cw(x))) + transx,t(Tij) (3.7) trong đó joinx(Tr,p,Ti-r,q ) là chi phí của phép kết nối ẩn giữa các kết quả Tr,p và

Ti-r,q ở trạm x và transx, t(Ti,j) là chi phí truyền kết quả của Ti,j từ trạm x tới trạm t.

Để chọn một kế hoạch tối ưu hóa trong số các kế hoạch được tạo ra lần lượt bởi buildJPlan và buildTPlan cần sử dụng nguyên lí tối ưu hóa: Nếu các kế hoạch chỉ khác trong các kế hoạch con, kế hoạch với kế hoạch con tối ưu là kế hoạch tối ưu. Nguyên lí này có thễ được diễn đạt một cách hình thức như sau:

Cost(al(x))<=( ∀u) Cost(au(x)) và Cost(bl(x))<=( ∀ v) Cost(bv(x))

=>Cost(buildJPlanx(al(x), bl(x)))<=(∀ u,v) Cost(buildJPlanx(au(x), bv(x))) (3.8) Cost(cl(x)))<=( ∀ w) Cost(cw(x)))

=> Cost(buildTPlan x,t(cl(x)))<=( ∀ w) Cost(buildTPlan x,t(cw(x))) (3.9)

Trong đó các kế hoạch con al(x), bl(x) và cl(x) lần lượt là các kế hoạch chi phí thấp nhất trong số các kế hoạch au(x), bv(x) và cw(x).

Định lí 3.1: Mô hình chi phí cho kế hoạch kết nối ẩn và kế hoạch truyền thỏa mãn nguyên lí tối ưu hóa.

Chứng minh: Để chứng minh định lí, chúng ta chứng minh biểu thức (3.8) và (3.9). Chứng minh cho công thức (3.8) như sau, trong đó bước 1 và bước 3 theo định nghĩa chi phí của buildJPlan và bước 2 là do giả thiết rằng Cost(al(x))<=Cost(au(x))

và Cost(bl(x))<=Cost(bv(x)) cho giá trị u và v tùy ý.

Cost(buildJPlanx(al(x), bl(x))) = Cost(al(x)) + Cost(bl(x)) + joinx(Tr,p, Ti-r,q)

<= Cost(au(x)) + Cost(bv(x)) + joinx(Tr,p, Ti-r,q)

<= Cost(buildJPlanx(au(x), bv(x)))

Chứng minh cho công thức (3.9) như sau, trong đó bước trong đó bước 1 và bước

3 theo định nghĩa chi phí của buildTPlan và bước 2 là do giả thiết rằng Cost(cl(x))<=Cost(cw(x)) cho giá trị w tùy ý.

Cost(buildTPlan x,t(cl(x))) = Cost(cl(x))) + transx,t(Ti,j)

<= Cost(cw(x))) + transx,t(Ti,j)

<= Cost(buildTPlan x,t(cw(x)))

3.4.5. Thuật toán tối ưu hóa PathExpOpt

Thuật toán bao gồm ba bước sau:

 Bước đầu tiên là khởi tạo

 Bước tiếp theo tìm phương án tối ưu cho các cây con cảm sinh, lần lượt từ các cây có một đỉnh đến cây có n đỉnh

 Bước cuối cùng thực hiện biểu thức đường dẫn theo kế hoạch tối ưu đã tìm ra

a. Khởi tạo

 Trong phần khởi tạo thực hiện rút gọn các lớp (hoặc các mảnh lớp) bằng các phép chiếu trên các thuộc tính cần để lại, các thuộc tính này thuộc một trong ba loại sau:

o Các OID của các lớp

o Các thuộc tính phức dùng để nối

o Các thuộc tính cần chọn lựa sau truy vấn

 Sinh các cây con cảm sinh và tính kích thước các cây con cảm sinh.

b. Tìm phương án tối ưu

- Bước 1: Khởi tạo chi phí các cây có một đỉnh, chi phí của cây một đỉnh tại mỗi trạm chính là chi phí truyền đỉnh đến trạm này.

- Bước 2: Xây dựng các phương án tối ưu cho các cây từ 2 đỉnh.

o Bước 2.1: Tìm phương án tối ưu thực hiện Ti,j qua các phép nối. Với mỗi cây Ti, j (Cây thứ j có i đỉnh) duyệt tất cả các cách tách cây thành 2 cây con cảm sinh Tr ,p và Ti-r, q, tìm cách tách mà chi phí Ti, j là nhỏ nhất. Chi phí Ti, j tại trạm t được tính bằng tổng chi phí Tr ,p và Ti-r, q tại trạm t và chi phí nối 2 cây này tại trạm t. Lưu lại phương án thực hiện tối ưu.

o Bước 2.2: Tìm phương án tối ưu thực hiện Ti, j qua các phép truyền. Chi phí Ti, j tại trạm t sẽ được tính lại nếu chi phí này lớn hơn tổng chi phí của Ti, j tại trạm x và chi phí truyền Ti, j từ trạm x tới trạm t. Lưu lại phương án thực hiện tối ưu.

Thuật toán 3.5 PathExpOpt Đầu vào:

- G =(V, E); V={F1, F2,…, Fn};

- fragSize: Mảng lưu kích thước của các mảnh

- fragSite: Mảng lưu trạm mà các mảnh định vị

- transCost: Mảng lưu chi phí giữa các trạm

- T: Các cây con cảm sinh của cây truy vấn ban đầu

- treeSize: Mảng kích thước các cây con, được tính khi sinh cây.

- k: Trạm phát sinh truy vấn

Đầu ra: Kế hoạch thực thi tối ưu cho cây truy vấn (result) Các bước của thuật toán:

//Bước 1: Khởi tạo chi phí các cây con 1 đỉnh for (u=1; u<=n; u++) //n là số các mảnh

begin

x = fragSiteu;

for (t = 1; t<=s; t++) //s là số các trạm Cost_Transt(T1,u)= fragSizeu * transCostx,t;

end; {for u}

//Bước 2: Xây dựng các phương án tối ưu cho các cây từ 2 đỉnh for (i=2; i<=n; i++)

//Bước 2.1: Tìm phương án tối ưu thực hiện Ti,j qua các phép nối for (j=1; ji; j++) //mi là số cây con cảm sinh có i đỉnh

for (t = 1; t<=s; t++)

JoinPlant(Ti,j)= Find_JoinPlan(Ti,j); end; {for t}

end; {for j}

//Bước 2.2: Tìm phương án tối ưu thực hiện Ti,j qua phép truyền

for (t = 1; t<=s; t++) for (j=1; ji; j++)

TransPlant(Ti,j)= Find_TransPlant(Ti,j); end; {for j}

end; {for t} end; {for i}

result = TransPlank(Tn,1); //k là trạm phát sinh truy vấn

end; {Thuật toán 3.5}

Thuật toán 3.6 Find_JoinPlan(Ti,j)

//Tìm phương án tối ưu thực hiện Ti,j thông qua các phép nối Đầu vào:

- G =(V, E); V={F1, F2,…, Fn};

- transCost: Mảng lưu chi phí giữa các trạm

- T: Các cây con cảm sinh của cây truy vấn ban đầu

- treeSize: Mảng kích thước các cây con, được tính khi sinh cây

Đầu ra: JoinPlant(Ti,j). Các bước của thuật toán:

//Tìm chi phí bé nhất của cây con cảm sinh Ti,j tại các trạm Cost_Joint(Ti,j)=∞;

//Duyệt các cách tách cây

for (each (Tr,p and Ti-r,q) that Ti,j = Tr, p ᴜ Ti-r,q) begin

//tính chi phí join Tr,p và Ti-r,q theo bộ lọc Bloom Cost_Temp = cost_BloomJoint(join(Tr,p,Ti-r,q);

if (Cost_Joint(Ti,j)>cost_Temp) begin

//lưu phương án chi phí nhỏ Cost_Joint(Ti,j)= cost_Temp; save JoinPlant(Ti,j);

end; {if}

end; {for each}

end; {Thuật toán 3.6}

Thuật toán 3.7 Find_TransPlan(Ti,j).

//Tìm phương án tối ưu thực hiện Ti,j thông qua các phép truyền Đầu vào:

- G =(V, E); V={F1, F2,…, Fn};

- transCost: Mảng lưu chi phí giữa các trạm

- T: Các cây con cảm sinh của cây truy vấn ban đầu

- treeSize: Mảng kích thước các cây con, được tính khi sinh cây

Đầu ra: TransPlant(Ti,j) Các bước của thuật toán:

//Xem xét nếu có phương án mà tổng chi phí join trên 1 trạm nào

//đó cộng với chi phí truyền đến trạm này nhỏ hơn thì thay thế Cost_Transt(Ti,j)= ∞;

for (x = 1; x<=s; x++)

begin

Cost_Temp = Cost_Joinx(Ti,j)+ treeSize(Ti,j)* transCostx,t; if (Cost_Transt(Ti,j)>cost_Temp)

begin

//thay thế nối tại t bằng nối tai x rồi truyền đến t Cost_Tempt(Ti,j)= cost_Temp;

save TransPlant(Ti,j); end; {if}

end; {for x}

end; {Thuật toán 3.7}

c. Thực hiện truy vấn theo kế hoạch tối ưu

Bằng cách lần ngược từ cây Tn,1 sẽ tìm ra kế hoạch tối ưu và thực hiện truy vấn theo kế hoạch tối ưu này. Trong quá trình thực hiện sử dụng bộ lọc Bloom để truyền dữ liệu.

3.4.6. Đánh giá độ phức tạp và cài đặt thuật toán

Độ phức tạp của thuật toán phụ thuộc vào số lớp, số trạm và số cây con cảm sinh được sinh ra. Trường hợp tốt nhất, đồ thị truy vấn là đồ thị chuỗi (tương ứng với truy vấn chuỗi) thì số cây con cảm sinh có i đỉnh là n-i+1, khi đó số các kế hoạch nối và kế hoạch truyền là:

𝑛 𝑛−𝑖+1 𝑠

𝑖−1

𝑠 𝑛−𝑖+1 𝑠

(𝑛 − 1)𝑛(𝑛 + 1) (𝑛 − 1)𝑛

∑( ∑ ∑ ∑ 𝑟 + ∑ ∑ ∑ 𝑥) = 𝑠 + 𝑠2

(3.10)

𝑖=2

𝑗=1

𝑡=1 𝑟=1

𝑡=1

𝑗=1

6 2

𝑥=1

𝑖−1

Như vậy độ phức tạp của thuật toán trong trường hợp tốt nhất là O(sn3). Trong trường hợp xấu nhất đồ thị truy vấn là đồ thị sao (tương ứng với truy vấn hình sao) thì số cây con cảm sinh 𝐶𝑛−1, độ phức tạp của thuật toán trong trường hợp này là

O(s2n-1).

𝑛

𝑛−1

𝐶

𝑖−1 𝑠

𝑖−1

𝑛−1

𝐶

𝑠 𝑖−1 𝑠

∑( ∑ ∑ ∑ 𝑟 + ∑ ∑ ∑ 𝑥) = 𝑠(𝑛 − 1)2𝑛−2 + 𝑠2(2𝑛−1 − 1) (3.11)

𝑖=2

𝑗=1

𝑡=1 𝑟=1

𝑡=1

𝑗=1 𝑥=1

Trong trường hợp đồ thị truy vấn có nhiều đồ thị con cảm sinh có thể sử dụng một heuristic cho thuật toán bằng cách chỉ xét các cách tách Ti,j thành các cây T1,p và Ti-1,q. Thử nghiệm cho thấy thời gian thực hiện thuật toán cho đồ thị hình sao 20 đỉnh từ 15 phút khi dùng heuristic trên chỉ còn chưa đến 1 phút, phương án thu được là phương án gần tối ưu với chi phí không chênh lệch nhiều so với phương án tối ưu.

Thuật toán đã được cài đặt bằng Java và kiểm thử với các truy vấn biểu thức đường dẫn liên quan đến số lớp là 20.

3.4.7. Kết quả thực nghiệm

Ví dụ về dữ liệu thực nghiệm và kết quả sinh ra như Hình 3.6. Dữ liệu thử nghiệm gồm tập 20 mảnh thuộc các lớp với kích thước và trạm đã được định vị, đồ thị kết nối là đồ thị với nhiều nút hình sao, mạng kết nối gồm 4 trạm với chi phí truyền mỗi đơn vị dữ liệu giữa 2 trạm được xác định trước.

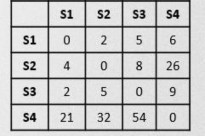
T[11,2492]: 4,7,5,6,10,11,16,17,18,19,20

1: T[1,4] + T[10,2312] = [12400, 17000, 25400, 4600]

2: T[1,5] + T[10,1850] = [6800, 8000, 5600, 8500]

3: T[1,16] + T[10,1388] = [6600, 5500, 7200, 9800]

4: T[1,17] + T[10,1387] = [6400, 7000, 5600, 7300]

5: T[1,18] + T[10,1386] = [14200, 18300, 27200, 6400]

6: T[1,19] + T[10,1385] = [6800, 8000, 5600, 9100]

7: T[1,20] + T[10,1384] = [8200, 5500, 10400, 20200]

8: T[3,5] + T[8,1346] = [7100, 6900, 7900, 5600]

9: T[4,6] + T[7,950] = [7600, 6900, 7800, 6100]

10: T[5,10] + T[6,515] = [8200, 8100, 7800, 6700]

- JOIN: [6400, 5500, 5600, 4600]

- J_PLAN: [[1,17]+[10,1387], [1,16]+[10,1388],

[1,5]+[10,1850], [1,4]+[10,2312]]

- TRANS: [5800, 5500, 5600, 4600]

- T_PLAN: [3, 0, 0, 0]

JOIN_2(F2,JOIN_2(F9,JOIN_2(F13,JOIN_2(F16,JOIN_2(F20,TRANS_1->2(JOIN_1(F8,JOIN_1(F14, JOIN_1(F15,TRANS_3->1(JOIN_3(F3,JOIN_3(TRANS_1->3(F1),JOIN_3(F5,JOIN_3(F17,JOIN_3(F19, TRANS_1->3(JOIN_1(TRANS_3->1(F12),TRANS_4->1(JOIN_4(F4,JOIN_4(F18,JOIN_4(F11,

TRANS_1->4(JOIN_1(F7,TRANS_2->1(JOIN_2(F6,TRANS_3->2(F10))))))))))))))))))))))))))

Hình 3.6: Minh họa kết quả thử nghiệm