Đơn Giản Hóa Các Phép Kết Nối Giữa Các Quan Hệ Được Phân Mảnh Ngang Chính

Các mảnh ngang là các ví dụ tiêu biểu của các quan hệ định tính, trong đó vị từ định tính tương ứng với vị từ phân mảnh.

Ví dụ 4.7: Xét lược đồ phân mảnh trong ví dụ 2.13, ta có các quan hệ định tính [PH1: MAP  10]; [PH2: MAP >10 AND MAP < 20].

[NCC1: DC = „Miền Bắc‟]; [NCC2: DC = „Miền Nam‟].

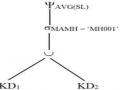
[KD1: KD.MANCC = NCC.MANCC  NCC. DC = „Miền Bắc‟] [KD2: KD.MANCC = NCC.MANCC  NCC. DC = „Miền Nam‟]

Vị từ định tính của một quan hệ không cần phải được định trị trên các bộ của quan hệ. Tuy nhiên, nếu vị từ định tính được định trị thì vị từ định tính phải đúng. Cụ thể, một vị từ định tính không thể được định trị khi chúng ta không địng trị được một số thuộc tính trong biểu thức của vị từ định tính.

Đại số các quan hệ định tính là sự mở rộng của đại số quan hệ, trong đó sử dụng các quan hệ định tính như là các toán hạng. Rò ràng, đại số này đòi hỏi việc thao tác trên các điều kiện định tính cũng như trên các quan hệ.

2) Các quy tắc

Các quy tắc sau đây xác định kết quả của việc áp dụng các phép toán đại số quan hệ cho các quan hệ định tính:

a) Quy tắc 1: F [R: qR]  [F R: F AND qR]

Có thể bạn quan tâm!

• Cơ sơ dữ liệu phân tán - 22
• Các Phép Biến Đổi Tương Đương Dùng Cho Các Truy Vấn
• Đồ Thị Toán Tử Và Xác Đinh Biểu Thức Con Chung
• Sử Dụng Phép Suy Diễn Cho Các Phép Đơn Giản Hóa
• Đơn Giản Hóa Các Truy Vấn Tham Số Và Mở Rộng Đại Số Quan Hệ
• Cơ sơ dữ liệu phân tán - 28

Xem toàn bộ 312 trang tài liệu này.

Quy tắc này phát biểu rằng việc áp dụng một phép chọn F cho một quan hệ định tính [R: qR] tạo ra một quan hệ định tính có quan hệ F R là thân của nó và vị từ F AND qR là vị từ định tính của nó. Việc mở rộng vị từ định tính F AND qR sau khi chọn phản ánh rằng F và qR đều được thỏa mãn trên tất cả các bộ được chọn.

b) Quy tắc 2: A [R: qR] A [R: qR]

Vị từ định tính của kết quả của một phép chiếu vẫn không thay đổi, ngay cả khi phép chiếu loại bổ một số thuộc tính dùng để định trị vị từ định tính. Lý do là các vị từ định tính mang thông tin ngữ nghĩa (intensional information). Do đó, điều này vẫn đúng khi loại bỏ các thuộc tính được dùng đẻ biểu diễn vị từ định tính, mà không loại bỏ chính định vị từ định tính

c) Quy tắc 3: [R: qR]  [S: qS]  [R  S: qR AND qS]

Việc mở rộng vị từ định tính qR AND qS là trực quan. Lưu ý rằng hai vị từ định tính áp dụng riêng cho các thuộc tính của R  S.

d) Quy tắc 4: [R: qR] - [S: qS]  [R - S: qR]

Việc mở rộng phép hiệu là hơi trực quan. Khi chúng ta loại bỏ các bộ của quan hệ S có trong quan hệ R, vì từ định tính của kết quả vẫn giống với vị từ định tính của R. Điều không đúng khi thay thế nó thành qr AND NOT qs, bởi vì có thể các bộ của R

không thỏa mãn qR AND NOT qS, nhưng nó có trong kết quả bởi vì S không chứa các bộ này.

Tuy nhiên, vấn đề sau đây được đặt ra với quy tắc 4:

Xét phép giao của hệ số quan hệ truyền thống, được định nghĩa là R  S = R - (R - S). Từ định nghĩa, dễ dàng thấy rằng phép giao có tính giao hoán, nghĩa là:

R  S = S  R

Nếu chúng ta áp dụng định nghĩa của đại số mở rộng, chúng ta đi đến 1 kết quả đáng ngạc nhiên:

[R: qR]  [S: qS]  [R: qR] - ([R: qR] - [S: qS]) 

[R: qR] - [R - S: qR]  [R (R - S): qR]  [R  S:qR] (4.2.a)

[S: qS]  [R: qR]  [S: qS] - ([S: qS] - [R: qR] 

[S: qS] - [S - R: qS]  [S- (S - R): qS] - [R: qR]  [S  R: qS] (4.2b)

Trên thực tế, kết quả mà chúng ta muốn tìm là. [R  S: qR AND qS]

Bởi vì các bộ của phép giao là những bộ thuộc cả hai quan hệ thỏa mãn cả hai qr và

qs. Lưu ý rằng, qr AND qs bao hàm cả hai qr và qs. Do đó, các kết quả (4.2a) và (4.2b) là không sai, nhưng dĩ nhiên một số thông tin bị mất.

e) Quy tắc 5: [R: qR]  [S: qS]  [R  S: qR OR qS]

Phép hợp được mở rộng bằng cách lấy OR của các vị từ định tính.

Cho trước các quy tắc trên, chúng ta thấy các phép toán đại số được suy đoán như thế nào, chẳng hạn phép kết nối và phép nửa kết nối. Chúng ta có thêm hai quy tắc

f) Quy tắc 6: [R: qR] [S: qS]  [R F S: qR AND qS AND F]

Chứng minh quy tắc 6 (nên nhớ rằng phép kết nối đựơc suy dẫn từ việc sử dụng phép chọn và tích Descarters).

[R: qR] [S: qS] 

F ([R: qR]  [S: qS] 

F [R  S: qR AND qS] 

F (R  S): qR AND qS AND F] 

[R: F S: qR AND qS AND F]

g) Quy tắc 7: [R: qR] F [S: qS]  [R F S: qR AND qS AND F]

Chứng minh quy tắc 7 (nên nhớ rằng phép nửa kết nối được suy dẫn từ việc sử dụng phép chiếu và phép kết nối)

[R: qR] F [S: qS] 

Atlr(R)([R: qR] F [S: qS]) 

Atlr(R)[R F S: qR AND qS AND F] 

[Atlr(R)(R F S): qR AND qS AND F] 

[R: F S: qR AND qS AND F]

Chứng minh hai quy tắc này sẽ cho chúng ta thấy cách thao tác các quan hệ định tính như thế nào.

3) Tính tương đương của hai quan hệ định tính

Hai quan hệ định tính là tương đương nếu các thân của chúng là các quan hệ tương đương và các vị từ định tính của chúng biểu diễn cùng hàm chân trị. Nghĩa là, nếu chúng ta áp dụng cả hai vị từ định tính cho cùng một bộ thì chúng ta có cùng một chân trị

Hệ quả: Tất cả các phép biến đổi tương của đại số quan hệ vẫn còn đúng với các đại số quan hệ định tính.

4) Các phép biến đổi tương đương để xác định một truy vấn là rỗng

Chúng ta sử dụng các vị từ định tính để loại bỏ các mảnh không liên quan đến truy vấn.

Xét vị từ định tính được tạo ra sau một phép chọn hoặc một phép chiếu. Trong những trường hợp này, vị từ định tính sẽ có dạng chuẩn giao các vị từ (conjunction of predicates). Vị từ định tính này có thể bị mâu thuẫn. Một ví dụ về một vị từ định tính mâu thuẫn là MAP =1 AND MAP= 5.

Các quan hệ định tính với các vị từ định tính mâu thuẫn về thực chất là rỗng. Điều nhận biết này là có ích hơn so với việc phát hiện ra kết quả của một biểu thức là rỗng khi thực hiện truy vấn.

Trên thực tế, sự mâu thuẫn là rút giảm các đặc tính ngữ nghĩa (intensional propety) của các mảnh, và có thể sử dụng trong lúc biên dịch truy vấn.

Bằng cách sử dụng các vị từ định tính ở trên, đại số quan hệ định tính sẽ cho các kết quả nhất quan mà các vị từ định tính của các toán hạng của nó được cho một cách đúng đắn và sẽ không biết trước kết quả như thế nào nếu các vị từ định tính là không đúng.

Vì chúng ta áp dụng đại số này cho các mảnh của các quan hệ, điều cảnh báo này cho thấy các vị từ định tính của các mảnh cần phải được cho trước một cách chính xác.

Ví dụ 4.8: Các biểu thức con dẫn đến quan hệ rỗng là:

DC = „Miền Nam‟ [NCC1: DC = „Miền Bắc‟]

[PH1: MAP < 10] MAP = MAP[NV3: MAP > 20]

Việc nhận biết một trong các biểu thức con của một truy vấn thực chất là rỗng sẽ dẫn đến các phép đơn giản hóa đáng kể của cây truy vấn.

Việc nhận biết một trong các biểu thức con của một truy vấn thực chất là rỗng sẽ dẫn đến các phép đơn giản hóa đáng kể của cây truy vấn. Các phép biến đổi tương sau đây là có ích, trong đó R có thể đựơc xem là một quan hệ thông thường hoặc một quan hệ định tính:

() 

A()  R  R R  R R -  R

 - R 

R F 

R F 

F R

Trong đó, R là một quan hệ thông thường hoặc một quan hệ định tính.

Việc nhận biết một trong các biểu thức con của một truy vấn thực chất là rỗng sẽ dẫn đến các phép đơn giản hóa đáng kể của cây truy vấn.

5) Các tiêu chuẩn để đơn giản hóa các biểu thức trên một lược đồ phân mảnh:

Tiêu chuẩn 1: Sử dụng tích lũy đẳng của phép chọn và phép chiếu để tạo ra các phép chọn và các phép chiếu thích hợp đối với mỗi quan hệ toán hạng.

Tiêu chuẩn 2: Đẩy các phép chọn và các phép chiếu xuống phía dưới cây nếu có thể được.

Tiêu chuẩn 3: Rút gọn với phép chọn

- Đẩy các phép chọn xuống phía các nút lá của cây

- Thực hiện chúng bằng cách dùng đại số quan hệ định tính

- Thay thế kết quả của phép chọn bởi quan hệ rỗng nếu vị từ định tính của kết quả bị mâu thuẫn.

Tiêu chuẩn 4: Sử dụng đại số quan hệ định tính để định trị vị từ định tính của các toán hạng của các phép kết nối.

Thay thế cây con (bao gồm phép kết nối và các toán hạng của nó) bằng quan hệ rỗng nếu vị từ định tính của kết quả của phép kết nối bị mâu thuẫn.

Tiêu chuẩn 5: Để phân tán các phép kết nối xuất hiện trong một truy vấn toàn cục, các phép hợp (biểu diễn việc tập hợp các mảnh) phải được đẩy lên phía trên các phép kết mà chúng ta muốn phân phối.

Năm tiêu chuẩn trên được dùng để đơn giản hóa các quan hệ được phân mảnh ngang đơn giản các phép kết nối giữa các quan hệ được phân mảnh ngang.

4.2.3. Đơn giản hóa các quan hệ được phân mảnh ngang

Các bước đơn giản hóa:

Bước 1: Tìm dạng chuẩn tắc của truy vấn

Bước 2: Đẩy phép chọn xuống phía các nút lá của cây

Bước 3: Rút gọn với phép chọn bằng cách loại bỏ phần chứa phép chọn sinh ra quan hệ rỗng

i

Cho quan hệ R được phân mảnh ngang chính thành R1, R2, ..., Rn, trong đó Ri= p (R), pi là vị từ chọn

Quy tắc rút gọn phép chọn

j

p (Ri)= nếu  u  R: (pi(u)pj(u)) Trong đó:

+ pi, pj là các vị từ chọn

+ u là một bộ của R

+ p(u): vị từ p đúng với u

Ví dụ 4.9: Xét hệ thống quản lý kinh doanh của một công ty với lược đồ phân mảnh trong ví dụ 2.13. Hãy đơn giản hoá câu truy vấn trên các mảnh:

Select * From PH

Where MAP=1

Ta có biểu thức đại số quan hệ tương ứng: Q3: MAP = 1(PH)

Bước 1: Dạng chuẩn tắc của truy vấn Q3

MAP = 1(PH1  PH2  PH3)

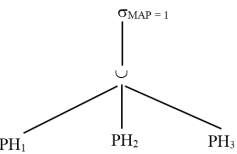
Bước 2: Đẩy phép chọn hướng xuống các nút lá bằng cách phân phối nó đối với phép hợp.

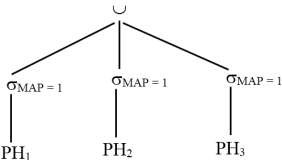
Bước 3: Rút gọn với phép chọn

MAP = 1(PH2) =  u  PH: (p2(u)pj(u))

p2(u): 10<MAP < 20 pj(u): MAP = 1

MAP = 1(PH3) =  u  PH: (p3(u)pj(u)) p3(u): MAP > 20

pj(u): MAP = 1

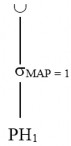
Bước 4: Đơn giản phép hợp

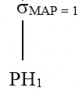
4.2.4. Đơn giản hóa các phép kết nối giữa các quan hệ được phân mảnh ngang chính

Các bước đơn giản hóa:

Bước 1: Tìm dạng chuẩn tắc của truy vấn theo hai giải pháp sau Giải pháp 1:

R F S = ( Ri) F ( Sj), nếu có nhiều mảnh được kết nối với nhau Giải pháp 2:

R F S =  (Ri F Sj), nếu có một số cặp mảnh được kết nối với nhau Bước 2: Đẩy phép hợp lên phía các phép kết nối

( Ri) F ( Sj)=  (Ri F Sj)

Bước 3: Rút gọn với phép nối bằng cách loại bỏ phần được tạo bởi phép kết nối sinh ra quan hệ rỗng.

Cho quan hệ R được phân mảnh ngang chính thành R1, R2, ..., Rn, trong đó

i

Ri= p

(R), pi là vị từ chọn

Quy tắc rút gọn phép nối

Ri F Rj =  nếu u  Ri, v  Rj: (pi(u)pj(v))

Trong đó

pi, pj là các vị từ chọn

u là một bộ của Ri, v là một bộ của Rj p(u): vị từ p đúng với u

Chú ý: Nếu phép kết nối là phép kết nối bằng thì sử dụng kí hiệu *.

Ví dụ 4.10: Xét hệ thống quản lý kinh doanh của một công ty với lược đồ phân mảnh trong ví dụ 2.13. Hãy đơn giản hoá câu truy vấn trên các mảnh:

Select *

Form KD, NCC

Where KD.MANCC= NCC.MANCC

Ta có biểu thức đại số quan hệ tương ứng: Q4: KD * NCC

Các bước đơn giản hóa:

Bước 1: Dạng chuẩn tắc của truy vấn Q4 (KD1 KD2) * (NCC1NCC2)

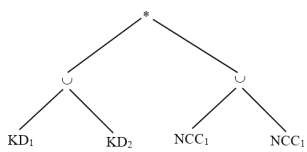
Bước 2: Đẩy phép hợp lên phía các phép kết nối

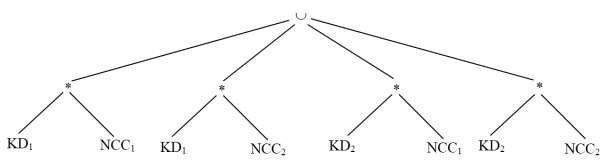
Bước 3: Rút gọn với phép nối KD1 * NCC2 = 

KD2 * NCC1 = 

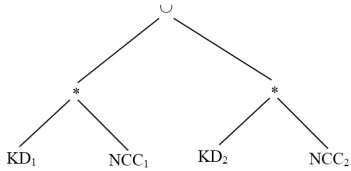
4.2.5. Đơn giản hóa cho phân mảnh ngang dẫn xuất

Các bước đơn giản hóa:

Bước 1: Tìm dạng chuẩn tắc của truy vấn

Bước 2: Đẩy phép chọn xuống phía dưới các nút lá của cây Bước 3: Rút gọn phép chọn, đơn giản phép hợp

Bước 4: Đẩy phép hợp lên phía các phép kết nối ( Ri) F ( Sj)=  (Ri F Sj)

Bước 5: Rút gọn với phép nối, đơn giản phép hợp

Ví dụ 4.11: Xét hệ thống quản lý kinh doanh của một công ty với lược đồ phân mảnh trong ví dụ 2.13. Hãy đơn giản hoá câu truy vấn trên các mảnh:

Select *

Form NCC, KD

Where NCC.MANCC = KD.MANCC and DC=”Miền Bắc”

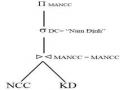
Ta có biểu thức đại số quan hệ tương ứng: Q5: NCC * DC=”Miền Bắc” KD

 KD * DC=”Miền Bắc” NCC

Các bước đơn giản hóa:

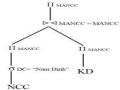
Bước 1: Dạng chuẩn tắc của truy vấn Q5 (KD1 KD2)* DC=”Miền Bắc” (NCC1  NCC2 )

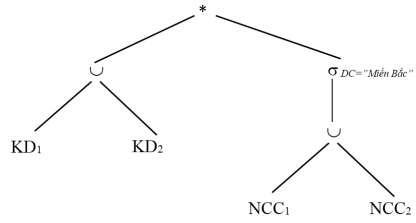
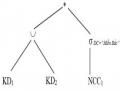
Bước 2: Đẩy phép chọn xuống phía dưới

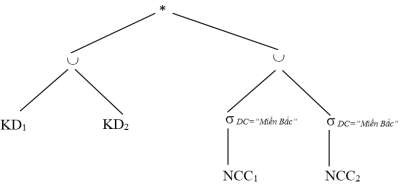
Bước 3: Rút gọn với phép chọn, đơn giản phép hợp

DC=”Miền Bắc” (NCC2)= 