q22 và cung đi ra có nhãn là A đang nối với nút có nhãn là q23 , không trùng với ký tự X nên quá trình duyệt chuyển sang cung đi ra khỏi q22 tiếp theo mang nhãn là B, không trùng với ký tự X nên quá trình duyệt chuyển sang cung đi ra khỏi q22 tiếp theo mang nhãn là C, không trùng với ký tự X nên quá trình duyệt chuyển sang cung đi ra khỏi q22 tiếp theo mang nhãn là D, ... Quá trình duyệt chuyển sang cung đi ra khỏi q22 tiếp theo mang nhãn là X trùng với ký tự kết thúc được trỏ bởi con trỏ trên xâu vào và đang nối với nút có nhãn là q23. Con trỏ trên xâu vào chuyển sang ký tự tiếp theo là 1, tức là ký tự đầu tiên của xâu 1$. Quá trình duyệt chuyển sang nút có nhãn là q23. Vì q23 là nút kết thúc của token letter nên quá trình duyệt chuyến sang nút có nhãn là q25 của sơ đồ chuyển id.
Trên sơ đồ chuyển của id đang ở nút q25 và cung đi ra có nhãn là letter đang nối với nút có nhãn là q25.
Vì letter là token, do đó quá trình duyệt chuyển sang duyệt trạng thái bắt đầu trong sơ đồ chuyển của token letter là q22 . Trên sơ đồ chuyển của letter đang ở nút q22 và cung đi ra có nhãn là A đang nối với nút có nhãn là q23, không trùng với ký tự 1 nên quá trình duyệt chuyển sang cung đi ra khỏi q0 tiếp theo mang nhãn là B, không trùng với ký tự 1 nên quá trình duyệt chuyển sang cung đi ra khỏi q22 tiếp theo mang nhãn là C, … Quá trình duyệt chuyển sang cung đi ra khỏi q22 cuối cùng của token letter mang nhãn là z không trùng với ký tự kết thúc được trỏ bởi con trỏ trên xâu vào.
Quá trình duyệt chuyển sang cung đi ra khỏi nút q25 có nhãn là digit. Vì digit là token, do đó quá trình duyệt chuyển sang duyệt trạng thái bắt đầu trong sơ đồ chuyển của token digit là q0 . Trên sơ đồ chuyển của digit đang ở nút q0 và cung đi ra có nhãn là 0 đang nối với nút có nhãn là q1, không trùng với ký tự 1 nên quá trình duyệt chuyển sang cung đi ra khỏi q0 tiếp theo mang nhãn là 1, trùng với ký tự kết thúc được trỏ bởi con trỏ trên xâu vào và đang nối với nút có nhãn là q1. Con trỏ trên xâu vào chuyển sang ký tự tiếp theo là $, tức là ký tự kết thúc xâu. Quá trình duyệt chuyển sang nút có nhãn là q1. Vì q1 là nút kết thúc của token digit nên quá trình duyệt chuyến sang nút có nhãn là q25 của sơ đồ chuyển id.
Quá trình duyệt đã duyệt hết xâu vào và quá trình duyệt đến được trạng thái kết thúc q25 của sơ đồ chuyển của token id nên nó thông báo thành công và trả lại cho giai đoạn phân tích cú pháp token id.
- Các trường hợp khác làm tương tự như trên.
b) Các sơ đồ tổng hợp
1) Digits
Có thể bạn quan tâm!
-
Chương trình dịch - 22 -
Chương trình dịch - 23 -
Chương trình dịch - 24 -
Chương trình dịch - 26 -
Chương trình dịch - 27 -
Chương trình dịch - 28
Xem toàn bộ 224 trang tài liệu này.
Thay sơ đồ 1 vào sơ đồ 2, thu được kết quả:
4,5,6
Start
0,1,2,3
Digits: q0
0,1,2,3
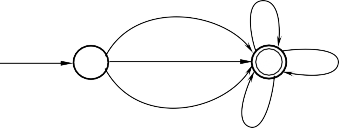
q1 4,5,6
7,8,9
7,8,9
2) Digitsign
Thay sơ đồ 1, sơ đồ 3 vào sơ đồ 4, thu được kết quả:
Digits:
Start q0
4,5,6
+, - ,
0,1,2,3
q1
0,1,2,3
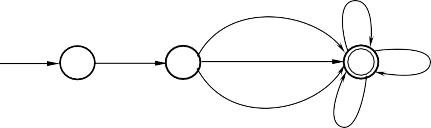
q2 4,5,6
3) Number
7,8,9
7,8,9
Thay sơ đồ 1 vào sơ đồ 5, thu được kết quả:
Start
q
0
+,- ,q
1
0,1,2,3,4
5,6,7,8,9
q
2
.
q3
0,1,2,3,4
5,6,7,8,9
q
4
number:
0,1,2,3,4 0,1,2,3,4
5,6,7,8,9
5,6,7,8,9
4) Nums
Thay sơ đồ 1 vào sơ đồ 6, thu được kết quả:
nums:
Start
q0
+,- ,
q1
0,...,9
q2 .
q 0,...,9
3
q
E
4
+,- ,
q5
q6
0,...,9
q7
0,...,9
0,...,9
0,...,9
5) id
Thay sơ đồ 1, sơ đồ 7 vào sơ đồ 8, thu được kết kết quả:
A, ..., Z
Start
9
A, ..., Z
a, ..., z
10
a, ..., z
id:
0, ..., 9
Hình BT 2.25
c) Sử dụng giải thuật sử dụng automat hữu hạn đơn định để nhận biết từ vị
CHƯƠNG 3
3.30. Lời giải tóm tắt
Áp dụng giải thuật khử đệ quy trái:
1. Sắp xếp các ký hiệu chưa kết thúc theo thứ tự S, A.
2. - Với i = 1:
+ j = 0 nên vòng lặp theo j bị bỏ qua
+ Loại bỏ đệ quy trực tiếp cho S, thu được: S AaS‟ | bS‟ và S‟ bS‟| .
- Với i = 2:
+ j = 1 và có luật sinh A Sd và tìm được S AaS‟ | bS‟. Nên sau khi thay A Sd, thu được: A Ab | AaS‟d | bS‟d | a.
+ Loại bỏ đệ quy trái trực tiếp cho A, thu được: A bS‟dA‟ | aA'; A' bA' | aS‟dA' | .
Văn phạm tương đương sau khi khử đệ quy trái gồm các luật sinh:
S AaS‟ | bS‟ và S‟ bS‟| ;
A bS‟dA‟ | aA'; A' bA' | aS‟dA' | .
3.31. Lời giải tóm tắt
1. Sắp xếp các ký hiệu chưa kết thúc theo thứ tự S, A, B.
2. - Với i = 1:
+ j = 0, vòng lặp j bị bỏ qua;
+ Khử đệ quy trái trực tiếp cho S- luật sinh:
Thay S Sc | Aa | Bb | a bằng S AaS‟ | BbS‟ | aS‟; S‟ cS‟| .
- Với i = 2:
+ j = 1:
* Không tồn tại luật sinh dạng A2 A1, lệnh if bị bỏ qua.
* Khử đệ quy trái trực tiếp cho A - luật sinh:
Thay A Ac| Bd| b bằng A BdA‟ | bA‟ ; A‟ cA‟| .
- Với i = 3:
+ j =1:
Tồn tại luật sinh B Sa và tìm được S AaS‟ | BbS‟ | aS‟ nên sau khi thay ta được: B Bb| AaS‟a | BbS‟a | aS‟a | c.
+ j = 2:
Tồn tại luật sinh B AaS‟a và tìm được A BdA‟ | bA‟ nên sau khi thay ta được: B Bb| BdA‟aS‟a | bA‟aS‟a | aS‟a |BbS‟a| c.
+ Loại bỏ đệ quy trái trực tiếp cho các B - luật sinh:
Thay luật sinh B Bb| BdA‟aS‟a | bA‟aS‟a | aS‟a | c bằng B bA‟aS‟a B‟| aS‟aB‟ | cB‟ và
B‟ bB‟| dA‟aS‟aB‟|bS‟aB‟| .
Vậy sau khi khử đệ quy trái ta thu được văn phạm với các luật sinh sau: S AaS‟ | BbS‟ | aS‟; S‟ cS‟| ;
A BdA‟ | bA‟ ; A‟ cA‟| ;
B bA‟aS‟a B‟| bS‟aB‟ | cB‟; B‟ bB‟| dA‟aS‟aB‟|bS‟aB‟| .
3.32. Hướng dẫn:
Tự làm, tương tự các bài: 3.30, 3.31.
3.33. Lời giải tóm tắt:
Áp dụng giải thuật thừa số hóa bên trái:
- Với biến S:
+ Thay S aaaAab | aaaAbb | aaaBC | aaC | Bcd | cad bằng S aaS1 | Bcd | cad;
S1 aAab| aAbb | aBC | C.
+ Với biến mới S1:
Thay S1 aAab| aAbb | aBC | C bằng S1 aS2 | C;
S2 Aab | Abb | BC.
+ Với biến mới S2:
Thay S2 Aab | Abb | BC bằng S2 AS3 | BC;
S3 ab | bb.
+ Với biến mới S3, không có tiền tố chung, kết thúc.
- Với biến A:
+ Thay A bbBa | bCc | ad bằng A bA1 | ad;
A1 bBa | Cc.
+ Với biến A1, không có tiền tố chung, kết thúc.
- Với biến B:
+ Thay B ccC | ccca bằng B ccB1;
B1 C | ca.
+ Với biến B1, không có tiền tố chung, kết thúc.
- Với biến C, không có tiền tố chung, kết thúc.
Kết quả thu được văn phạm tương đương, đã thừa số hóa bên trái với tập các luật sinh:
S aaS1 | Bcd | cad; S1 aS2 | C; S2 AS3 | BC; S3 ab | bb; A bA1 | ad; A1 bBa | Cc;
B ccB1; B1 C | ca;
C b | .
3.34. Lời giải tóm tắt:
Áp dụng giải thuật thừa số hóa bên trái:
- Với biến S:
+ Thay S aaaAab | aaaAbb | aacBC | bbaC | bbBcd | cad bằng S aaS1 | bb S2 | cad;
S1 aAab | aAbb | cBC;
S2 aC | Bcd.
+ Với biến mới S1:
Thay S1 aAab | aAbb | cBC bằng S1 aAS3 | cBC;
S3 ab | bb.
+ Với biến mới S3, không có tiền tố chung, kết thúc.
+ Với biến mới S2, không có tiền tố chung, kết thúc.
- Với biến A:
+ A bbBa | bbCc | abAd| aaC | c bằng A bbA1 | a A2 | c;
A1 Ba | Cc;
A2 bAd| aC.
+ Với biến A1, không có tiền tố chung, kết thúc.
+ Với biến A2, không có tiền tố chung, kết thúc.
- Với biến B:
+ Thay B ccbC | ccca | bB bằng B ccB1| bB;
B1 bC | ca.
+ Với biến B1, không có tiền tố chung, kết thúc.
- Với biến C:
+ C ab | ba | a | b bằng C aC1 | bC2;
C1 b| ;
C2 a| .
Kết quả thu được văn phạm tương đương, đã thừa số hóa bên trái với tập các luật sinh:
S aaS1 | bb S2 | cad; S1 aAS3 | cBC; S2 aC | Bcd; S3 ab | bb; A bbA1 | a A2 | c; A1 Ba | Cc; A2 bAd| aC;
B ccB1| bB; B1 bC | ca;
C aC1 | bC2; C1 b| ; C2 a| .
3.35. Lời giải tóm tắt:
Áp dụng giải thuật phân tích cú pháp đệ quy xuống:
- Khởi tạo:
+ Loại bỏ đệ quy trái:
Văn phạm trên không đệ quy trái.
+ Thực hiện thừa số hoá bên trái, thu được văn phạm tương đương: S bbABc;
A aA1 b;
A1 b| ;
B baB1 aB2 c; B1 c a;
B2 b c.
- Thực hiện giải thuật với các xâu được các cây phân tích cú pháp:
a) w = bbabacc b) w = bbbbabc
S
S
b b A a
B c
A1 a B2
b c
b b A B c
b b a B1 a
a) b)
c) w = bbabaac d) w = bbabaac
S
S
b b A Bc
b b A B c
a A1 b
a B1
b a B2
a b
c) d)
Hình BT 3.35. Cây phân tích cú pháp của các xâu
được xây dựng từ trên xuống theo phương pháp đệ quy xuống
3.36. Lời giải tóm tắt
Áp dụng giải thuật phân tích cú pháp đệ quy xuống:
- Khởi tạo:
+ Loại bỏ đệ quy trái, thu được văn phạm: S aBS1 aS1;
S1 AaS1 ;
A ab a b;
B bac bad a b.
+ Thực hiện thừa số hoá bên trái, thu được văn phạm tương đương: S aS2; S2 BS1 S1; S1 AaS1 ;
A aA1 b; A1 b | ;
B bB1 a ; B1 aB2 ; B2 c d.
- Thực hiện giải thuật với các xâu: