Pass-Through From Rediscount Rate To Deposit And Lending Rates

Figure 3.4: Correlation between refinancing interest rate and deposit interest rate at Agribank in the period 2008-2015

twelfth

ten

2008 2009 2010 2011 2012 2013 2014 2015

1M 6M 12M

18M 24M LSTCV

(Source: Agribank, State Bank of Vietnam for the period 2008-2015) In 2008, Agribank's deposit interest rate was always higher than the SBV's refinancing rate because Agribank's deposit interest rate fluctuated and increased sharply. and especially reached 17.5% in July and August. However, in the last months of 2008, Agribank's deposit interest rate was close to the refinancing rate. In the period from 2009-2011, the difference between Agribank's deposit interest rate was about 3-4% higher than the refinancing rate. The reason is that Agribank's deposit interest rate in 2009 fluctuated according to the yield curve with the longer the deposit interest rate, the higher it is, specifically, the deposit interest rate ranged from 6%-8.6%, for 3 months alone. At the end of 2009 due to high liquidity demand, deposit interest rates increased sharply to 10.4%. Movements of the money market at the end of 2010- early 2011 showed that, Due to the low liquidity of credit institutions, many credit institutions race to increase deposit interest rates to compete for market share, attract idle money from the population and economic organizations, and cause disturbances to the money market. In that trend, Agribank's deposit interest rates for terms also increased to 14%/year. Especially in the period 2011-2013, Agribank's deposit interest rate closely followed the change of the refinancing interest rate and the refinancing interest rate was higher than the deposit rate, reflecting the true nature of the interest rate. refinancing is the guide to adjust market interest rates of the State Bank. In the period 2013-2015, Agribank's deposit interest rates for terms also increased to 14%/year. Especially in the period 2011-2013, Agribank's deposit interest rate closely followed the change of the refinancing interest rate and the refinancing interest rate was higher than the deposit rate, reflecting the true nature of the interest rate. refinancing is the guide to adjust market interest rates of the State Bank. In the period 2013-2015, Agribank's deposit interest rates for terms also increased to 14%/year. Especially in the period 2011-2013, Agribank's deposit interest rate closely followed the change of the refinancing interest rate and the refinancing interest rate was higher than the deposit rate, reflecting the true nature of the interest rate. refinancing is the guide to adjust market interest rates of the State Bank. In the period 2013-2015,

Agribank has always taken the lead in lowering deposit interest rates lower than the ceiling prescribed by the State Bank. Typically, the 1-month deposit interest rate is much lower than the refinancing rate, only 4-5%/year, the difference is about 2-3% lower than the refinancing rate.

This shows that the operating mechanism of the ceiling deposit interest rate of the State Bank plays an important role in stabilizing the market interest rate level in times of difficulty in liquidity of credit institutions, gradually reducing the interest rate level. according to the objectives of monetary policy management of the State Bank. However, the deposit rate ceiling also has some limitations such as at one time causing damage to savers due to negative real deposit rates. Therefore, other investment channels such as securities, real estate, gold became more attractive and some commercial banks broke the ceiling of deposit interest rates by spending more commissions, receiving disguised entrusted investments... This leads to tight liquidity and banks racing to compete for hidden interest rates. Therefore, the SBV's refinancing interest rate was at times lower than Agribank's deposit rate and could not keep up with market interest rates.

Figure 3.5: Correlation between refinancing interest rates and lending rates at Agribank in the period 2008-2015

twelfth

ten

2008 2009 2010 2011 2012 2013 2014 2015

LSNH LSTDH LSTCV

(Source: Agribank, State Bank of Vietnam for the period 2008-2015) Agribank's lending interest rate is always much higher than the refinancing rate of the State Bank. The reason is due to deposit interest rates in 2008 and 2010-

2012 is always high due to volatile market movements, leading to high interest rates. The peak in 2008 refinancing interest rate was only 15%/year, the lending interest rate reached nearly 21%/year or in early 2011 the refinancing interest rate was only 14%/year but the lending interest rate reached 20 years. Agribank's lending interest rates have always tried to keep up with the refinancing rate, but the difference is always about 3-5% higher in periods of strong increase in lending rates. Especially from the beginning of 2013 until now, the refinancing interest rate has decreased to only 6.5%/year, although short-term lending interest rate has decreased to 10%/year, medium and long-term lending interest rate has decreased by only 12%/year. year because Agribank has always been at the forefront of sharply reducing lending rates to support and restore production, helping to restore economic growth.

3.4.2 Pass-through from rediscount rate to deposit and lending rates

Figure 3.6: Correlation between rediscount interest rate and deposit interest rate at Agribank in the period 2008-2015

twelfth

ten

2008 2009 2010 2011 2012 2013 2014 2015

1M 6M 12M

18M 24M LTC

(Source: Agribank, State Bank of Vietnam for the period 2008-2015) The deposit interest rate of Agribank is always higher than the discount rate of the State Bank. Rediscount interest rate increased to 13%/year in the middle months of 2008 and at the same time, Agribank's deposit rate also increased because inflation showed signs of increasing again, peaking at nearly 19%/year. Faced with that situation, the State Bank actively implemented tightening monetary policy in order to stabilize the economy and control inflation. Thanks to the measures

Due to the drastic direction of the State Bank, by the end of 2008- early 2009, Agribank's deposit interest rate was close to the rediscount rate, the deposit interest rate dropped sharply to only about 7-8%/year. In 2010, the rediscount interest rate tended to decrease gradually, ranging from 5% to 6%/year, however, Agribank's deposit interest rate was still higher than the rediscount rate by nearly 5% because deposit interest rates tend to increase again. Entering 2011, the macroeconomic situation faced many difficulties, inflation increased, the banking system faced increasing risks, notably credit risk, exchange rate risk and credit risk. interest rates, many credit institutions faced liquidity difficulties due to high bad debts, causing unsafety to the banking system. Rediscount interest rate increased by nearly 12-13%, Agribank's interest rate increased by nearly 14%/year. Inflation has peaked in 2011, then in 2013, inflation will decrease, leading to a decrease in interest rates, so the rediscount interest rate will also decrease sharply, reaching 4%/year. Due to Agribank's abundant mobilized capital and good liquidity, Agribank proactively adjusted its short-term deposit interest rates, while long-term deposit rates also decreased to minimize costs. raise capital.

Figure 3.7: Correlation between rediscount interest rate and lending interest rate at Agribank in the period 2008-2015

twelfth

2008 2009 2010 2011 2012 2013 2014 2015

LSNH LSTDH LSTCK

(Source: Agribank, State Bank of Vietnam for the period 2008-2015)

Agribank's lending interest rate is always much higher than the SBV's rediscount rate. There were periods of high inflation and unstable economic situation such as 2008, late 2011- early 2012, lending interest rate of Agribank could not keep up with the change of rediscount interest rate, so there was a big difference. between the rediscount interest rate and the lending interest rate is quite large, close to 7%-8%/year. Faced with that situation, the State Bank has implemented many synchronous measures to achieve the goal of reducing the lending interest rate, removing difficulties for businesses and households, and flexibly adjusting the rediscount interest rate. combine administrative measures in line with market developments. Along with the SBV's efforts to reduce the rediscount interest rate,

Conclusion of chapter 3

Chapter 3 presents the current state of pass-through from interest rate policyof the State Bank to deposit rates and lending rates at Agribank for the period 2008-2015. This was the period when the economy was in financial crisis in 2008, so the economic situation was difficult. The SBV had to continuously use tools to stabilize the economy until 2012 before inflation would cool down. Therefore, interest rates also fluctuated according to the inflation situation, increasing continuously from 2009-2012 over 14%/year. On the basis of analyzing the current situation of the relationship between refinancing and rediscount interest rates to deposit rates and lending rates at Agribank, it shows that interest rates play an important role in operating monetary policy of the State Bank. The next chapter will apply the ARDL model to study the transmission from the SBV's interest rate policy to Agribank's deposit and lending rates in the long and short term from a quantitative perspective.

CHAPTER 4. METHODS, DATA AND RESEARCH RESULTS

Chapter 4 Introduction

In Chapter 4, the ARDL model is used to study the transmission from the interest rate policy of the State Bank to the deposit and lending rates at Agribank in the long and short term. The steps include testing for stationarity, testing for cointegration and determining the delay of the model. Finally, it measures the pass-through from refinancing interest rates to deposit and lending rates in the long term and short term; The pass-through from the discount rate to the deposit rate, the short-term and long-term lending rates, the rate of adjustment to long-run equilibrium, and the consideration of interest pass-through asymmetry short-term interest rate or not.

4.1 Autoregressive model of delayed distribution ARDL

There are many research models on interest rate pass-through in the world such as ECM equilibrium correction model, VECM model, VAR, SVAR or other variations of VAR model. When dealing with time series of data, we must consider the stationarity of the data. However, testing for stationarity in time series is of low reliability. Related to this issue, the method that has received much attention in recent years is the self-regressive and lagged boundary test method, also known as the ARDL boundary test of Pesaran and Shin (1999). ), then further developed by Shin et al (2001). The ARDL test has the following advantages:

- Requires a smaller sample size than other cointegration test methods.

- If the unit root test is considered a necessary step in the cointegration test methods, then in this method it is not necessary and can be omitted, the variables can be integrated to create order 0 or 1. The long-run relationship is tested based on two boundary values. In which, the lower boundary is the limit point where all variables integrate at degree 0 and the upper boundary is the limit point where all variables integrate at order 1.

- The ARDL approach provides unbiased long-run estimates if some of the model regressions are endogenous.

- Provides a method to evaluate the short-term and long-term impact of one variable on another variable.

Therefore, the thesis uses the ARDL model to study the level of pass-through from the interest rate policy of the State bank to the deposit and lending rates at Agribank in the short and long term.

4.2 Research Methods

Descriptive statistical method: Based on data collected in the period 2008-2015 to analyze the relationship between variables in the research model.

Approach to the ARDL delay distribution regression model:

Step 1: Check the stationarity of the data series to make sure that none of the variables integrate at order 2. Because the regression can be spurious if the variables are stationary at the order differential.

2. If the series stop together after taking the first difference, switch to testing the cointegration relationship between the data series according to the Bound Test method. Check the contour according to the following equation:

y t = β 0 + β i Δy t-i + j x t -j + 1 y t-1 + 2 x t-1 + e t (1)

Hypothesis :

H 0: There is no cointegration relationship, that is, between the variables, there is no relationship in the long run.

H 1: There exists a cointegration relationship, that is, between the variables there is a long-run relationship.

To test the null hypothesis , compare the value of the F-statistic (F-statistic) with the lower bound limit value (with the assumption that all variables are integrated at degree 0) and the upper bound value . (corresponding to the assumption that all variables are integrated of order 1).

+ If F > value of upper envelope corresponding to I(1), hypothesis H 0 is rejected. It is concluded that a cointegration relationship exists.

+ If F < value of the lower envelope corresponding to I(0), then H 0 is accepted. Conclusion There is no cointegration relationship.

+ If the value of the lower envelope < F < the value of the upper envelope, no conclusions can be drawn.

Step 2: Determine the optimal delay

Step 3: Estimate the long-run equation according to the ARDL model. The long-term relationship between Agribank's deposit rate, lending rate and the SBV's operating interest rate is described as follows:

y t = α 0 + α 1 x t + t ( 2)

In there:

y t (dependant variable): deposit rate or lending rate. x t (independent variable): refinancing or rediscount rate.

ԑ t : error or residual.

α 0 : the coefficient of freedom indicating how the mean value of y will change when x=0.

α 1 : coefficient measuring the level of pass-through in the long run. (according to Rousseas 1985). The degree of long-term pass-through is complete if statistically α 1 = 1.

Pt (2) is a model built in the long run. When monetary policy changes, the SBV will not adjust their operating rates immediately. Short-term interest rates are expected to adjust more quickly than medium- and long-term rates because medium and long-term rates depend on future short-term rates as well as current short-term rates.

Step 4: Estimating the short-term coefficient according to the unlimited error correction model UECM

To analyze the fluctuation of deposit and lending interest rates of Agribank before the change of refinancing and rediscount interest rates, the UECM structural error correction model is applied.

The general UECM unlimited error correction equation has the following form:

(3)

In there:

∆x t : difference of order 1

ε t - 1 =: adjusted error of the ECM model, represents the imbalance at time (t-1) and it represents the residual of the long-run relationship given by equation (1).

υ t : error.

β 0 : measure the ratio of the transmission mechanism, β i and γ i : coefficient of variation adjustment.

δ: error correction rate when the ratio is different from their equilibrium.

The sign of δ is expected to be negative due to the self-correcting nature of the mean of interest rates. The absolute value of δ indicates how quickly it is to remove the imbalance in the retail interest rate setting. The higher the elasticity of demand for commercial banks' products, the higher the cost to keep the commercial bank's interest rate from the equilibrium level and the higher the adjustment level of deposit and lending rates to changes in operating interest rate faster.

MAL (mean adjustment lag) - the average adjustment delay of the adjustment to the equilibrium point, calculated according to the formula of Hendry (1995). For the special case of an ARDL model, the formula is simplified as follows:

MAL = (β 0 -1) /

The MAL is the weighted average of all lags and it measures the rate at which the commercial bank rate reacts to changes in policy rates. According to research by Chong, 2005 and Scholnick, 1996, in the short run, the adjustment may be asymmetric. In other words, the rate of adjustment can be different when interest rates are above equilibrium and when interest rates are below equilibrium. To test for the existence of asymmetric adjustments in deposit and lending rates of commercial banks, the dummy variable λ is added to formula (3). λ =1 if the residual ε t-1 is positive and otherwise it will be 0. The short-run asymmetry equation is as follows:

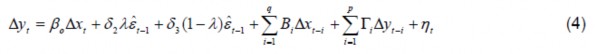
In there:

δ 2 : error correction speed when interest rates are higher than the equilibrium value.

δ 3 : error correction speed when interest rates are lower than the equilibrium value.

To test the existence of asymmetric adjustment, the author uses Wald's test to determine whether δ2 is significantly different from δ3 or not. As with the asymmetric correction case, we can determine the asymmetric mean correction lag (MAL) for the full pass-through from retail money market interest rates using the Hendry formula ( 1995). For the special case of the ARDL model, it is calculated as follows:

MAL + = ( β 0 -1) / 2

MAL - =( β 0 -1) / 3

Where MAL+ represents the average correction lag when retail interest rates are above equilibrium and MAL - represents the average correction lag when retail rates are below equilibrium.

4.3 Data collection and processing

Research data includes:

- The dependent variable is the deposit interest rate of Agribank for terms of 1 month (HĐ1M), 6 months (HĐ6M), 12 months (HĐ12M), 18 months (HĐ18M), 24 months (HĐ24M) and Agribank's lending interest rate. including short-term lending interest rate (CVNH), medium and long-term lending interest rate (CVTDH) announced by Agribank, collected from Agribank's notices on adjustment of deposit and lending interest rates from January 1. 2008 – December 2015.

- The independent variable is the operating interest rate of the State Bank, including the refinancing interest rate (representing the ceiling interest rate), the rediscount interest rate (representing the floor interest rate) announced by the State Bank of Vietnam, collected from Official website of the State Bank of Vietnam: www.sbv.gov.vn.

- Research period from January 2008 to December 2015.

The sample size is a series of 96 months.

4.4 Descriptive statistics of data

Table 4.1: Statistical results describing deposit and lending interest rates at Agribank in the period 2008-2015

Unit: %

	1M	6M	12M	18M	24M	SMALL	TDH
Medium	8,993021	9,666979	10,04052	9,738542	9,755000	12,98328	14,08740
Median	8,140000 won	8,640000	9,650000 won	9,730000 won	9,730000 won	11,200000	12,72500
Biggest	17,50000	17,50000	17,50000	17,50000	17,50000	21,00000 won	21,00000 won
Smallest	4,000000	5,30000 won	6,000000	6.20000	6,30000 won	9,000000	10,50000 won
Differrence	3.844662	3.297293	3.038562	2.452714	2.403539	3.456668	3.257457
Irregular coefficient symmetry	0.415382	0.649823	0.601143	0.728301	0.808288	0.832536	0.655379
Degree coefficient sharp	2.016644	2.464302	2.605022	3.542912	3.690190	2.334457	2.082540
Jarque- Bera	6.628637	7.904205	6,405992	9.665761	12,35871	12.81404	10.23927
Probability	0.036359	0.019214	0.040640	0.007964	0.002072	0.001650	0.005978
Total	863.3300	928,0300	963.8900	934,9000	936.4800	1246,395	1352,390
Square total	1404.235	1032,854	877.1215	571.5014	548,8148	1135,112	1008,047
Observe	96	96	96	96	96	96	96

Maybe you are interested!

(Source: Appendix 01) Table 4.2: Statistical results describing the refinancing and rediscount interest rates of the State Bank of Vietnam in the period 2008-2015

Unit: %

	TCV	TCK
Medium	9,119792	7,145833
Median	8,000000	6,000000
Biggest	1,50000 won	1,30000 won
Smallest	6,50000 won	4,50000 won
Differrence	2,880739	2.937880
Asymmetry coefficient	1.014121	1.023415
Sharpness coefficient	2.506139	2.491016
Jarque-Bera	1.743066	1.779431
Probability	0.000164	0.000137
Total	8,755000	6,860000 won
Sum squared	7.883724	8,199583

(Source: Appendix 01)

- The average value of the variables of short-term deposit interest rates 1M, 6M, 12M gradually increased, long-term deposit rates like 18M, 24M gradually decreased, medium and long-term LSCV was higher than short-term. The average of the rediscount interest rate is 7,145833%, the refinancing rate is 9,119792%.

- Two statistical values including the coefficient of asymmetry (Skewness) and the coefficient of kurtosis (Kurtosis) help us visualize the shape of the distribution. Skewness is an index that measures the skewness of the distribution, if: Skewness =0: symmetrical distribution, Skewness

>0: right skewed distribution, Skewness <0: left skewed distribution.

Kurtosis measures the relative concentration of observations around its center, if: Kurtosis =3: normally distributed, Kurtosis >3: more concentrated than normal distribution (polymorphism). Tall and pointed with 2 narrow tails, Kurtosis <3: less concentrated distribution than normal (obtuse polygon with two long tails).

All variables including deposit rate, lending rate, refinancing rate, and rediscount rate are all right skewed and less concentrated distribution than normal with obtuse polygon with two long tails.

Table 4.3: Correlation matrix between refinancing interest rate, rediscount interest rate and deposit and lending interest rates at Agribank in the period 2008-2015

Unit: %

	1 month contract	Contract 6M	Contract 12M	Contract 18M	HD24M	CVNH	CVTDH	TCV	TCK
1 month contract	first	0.9860002 5	0.9775580 7	0.9594494 8	0.9601005 2	0.92831843	0.8871444 5	0.85451099	0.85341449
Contract 6M	0.9860002 5	first	0.9833814 6	0.9580505 2	0.9572202 8	0.93106680	0.8917593 0	0.86680512	0.86454221
Contract 12M	0.9775580 7	0.9833814 6	first	0.9713554 2	0.9699700 2	0.93104467	0.9021858 6	0.88115188	0.88360978
Contract 18M	0.9594494 8	0.9580505 2	0.9713554 2	first	0.9986966 4	0.88771795	0.8584250 2	0.82539956	0.81836423
HD24M	0.9601005 2	0.9572202 8	0.9699700 2	0.9986966 4	first	0.89112600	0.8544532	0.83071860	0.82370299
CVNH	0.9283184 3	0.9310668 0	0.9310446 7	0.8877179 5	0.8911260 0	first	0.9782011 0	0.89211298	0.90256330
CVTDH	0.8871444 5	0.8917593 0	0.9021858 6	0.8584250 2	0.8544532	0.978201210	first	0.86147700	0.87114330
TCV	0.8545109 9	0.8668051 2	0.8811518 8	0.8253995 6	0.8307186 0	0.89211298	0.8614770 0	first	0.98795120
TCK	0.8534144 9	0.8645422 first	0.8836097 8	0.8183642 3	0.8237029 9	0.90256330	0.8711433 0	0.98795120	first

(Source: Appendix 01)

- The correlation matrix shows that deposit interest rates and short-term, medium- and long-term lending rates have a strong correlation with each other and with interest rates.

refinancing or the discount rate. This allows building a linear regression function between the series of deposit rates or lending rates with refinancing or rediscount rates.

4.5 Testing of ARDL . distributed delay autoregression model

4.5.1 Testing the stationarity of the data series through the unit root test method

Before analyzing the model, it is necessary to perform a stationarity test of the variables to avoid the case of false correlation, leading to skewed statistical tests. Consider the following model: Y t = Y t-1 + t ( -1≤ ρ ≤1) (5) Y t is a stationary series, then the mean, variance and covariance (at different lags) each other) will be the same at any point in time.

Assumptions:

H 0 : ρ =1 ( Y t is a non-stationary series) H 1 : ρ < 1 (Y t is a stationary series)

Equation (5) is equivalent to the following equation: Y t – Y t-1 = ρY t-1 – Y t-1 + t

∆Y t = ( -1 )Y t-1 + t

∆Y t = + t

Thus, the above assumptions can be rewritten as follows: H 0 : δ =0 ( Y t is a non-stationary series)

H 1 : < 0 (Y t is stationary series)

Dickey Fuller suggested that the estimated t value of the coefficient Y t-1 would follow the probability distribution τ ( tau statistic, τ = estimated δ value/ error of the coefficient δ ). The τ test is also known as the Dickey Fuller (DF) test. If | | > | α | _ (value τ look up the table) then reject H 0 , that is, the series Y t is stationary. Y t is said to be of first order if ∆Y t is a stationary series, denoted I(1). However, since there can be a series of correlations between u ts due to the lack of variables, the extended DF test is often used as ADF.

Table 4.4: Results of testing the stationarity of the original series of deposit interest rates and lending rates using the ADF . method

Unit: %

Original String	t-Statistics	Prob*	Conclude
1 month contract	-2.027167	0.2749	Don't stop
Contract 6M	-2.357899	0.1565	Don't stop
Contract 12M	-1.392710	0.5828	Don't stop
Contract 18M	-1.563726	0.4971	Don't stop
HD24M	-1.615662	0.4707	Don't stop
CVNH	-1.826436	0.3657	Don't stop
CVTDH	-2.066375	0.2587	Don't stop
TCV	-2.570517	0.1028	Don't stop
TCK	-1.551138	0.5035	Don't stop

(Source: Appendix 02) Table 4.5: Results of testing the stationarity of the series of differences in deposit and lending interest rates by ADF method

Unit: %

Differential series	t-Statistics	Prob*	Conclude
1 month contract	-12.585569	0.0000	Stop
Contract 6M	-11.58997	0.0000	Stop
Contract 12M	-15.07362	0.0000	Stop
Contract 18M	-14.64223	0.0000	Stop
HD24M	-14,86575	0.0000	Stop
CVNH	-7.787872	0.0000	Stop
CVTDH	-12,64119	0.0000	Stop
TCV	-10,39409	0.0000	Stop
TCK	-9.973895	0.0000	Stop

(Source: Appendix 02)

The stationarity of the original series reflects the long-run relationships around their expectations and variances. The stationarity of the differential series reflects the short-run relationships around expectations and their variances. The results show that the new differential series is stationary, so it can only be considered in the short term. If the original sequences come together as vectors with stable remainders, then a long-run relationship exists. To check this, it is necessary to perform a cointegration test.

4.5.2 Cointegration test

Table 4.6: Contour test results

Unit: %

Level of mind means	ten%	5%	2.5%	first%
I1	3.51	4.16	4.79	5.58
I0	3.02	3.62	4.18	4.94
TCK	1 month contract	Contract 6M	Contract 12M	Contract 18M	HD24M	CVNH	CVTDH
F-statistics	9.5058	13.326	19,787	15,522	17,213	69.24	26.612
TCV	1 month contract	Contract 6M	Contract 12M	Contract 18M	HD24M	CVNH	CVTDH
F-statistics	19.4348	13.4721	35,998	24.0446	5.6063	24,485	24.495

(Source: Appendix 03) The F-statistical values of all variables of deposit interest rate, lending interest rate in correlation with refinancing interest rate, rediscount interest rate are all greater than the upper envelopeI1 corresponds to a significance level of 5%. Therefore, hypothesis H 0 is rejected, which means that there exists a long-run relationship between the variables in the model.

4.5.3 Diagnostic test and residual test

For the model to estimate reliably, the residuals of the model must be free of autocorrelation and variable variance. Therefore, the author conducts Lagrange test to detect autocorrelation and White test to detect variable variance.

Hypothesis: