Lý Thuyết Cơ Bản Về Lập Lịch Dựa Trên

- Tính toán tình nguyện có những máy chủ trung tâm. Điển hình là không có truyền thông ngang hàng.

- Tính toán ngang hàng mang lại lợi ích cho những người tham gia. Ở đó không có khái niệm 1 dự án mà tài nguyên được cung cấp miễn phí.

- Tính toán ngang hàng thật sự bao gồm sự tích trữ và lấy lại, không phải tính toán.

Chương 2. LÝ THUYẾT CƠ BẢN VỀ LẬP LỊCH DỰA TRÊN

ĐỘ TIN CẬY

Trong phần này, tôi tóm tắt lại mô hình cơ bản và các giả định, các kĩ thuật chịu lỗi truyền thống, các kĩ thuật chịu lỗi dựa trên độ tin cậy cho tính toán tình nguyên và khảo sát một số giản đồ lập lịch chịu lỗi dựa trên độ tin cậy.

Có thể bạn quan tâm!

Xem toàn bộ 83 trang tài liệu này.

2.1 Mô hình cơ bản và các giả định

Mô hình tính toán. Trong luận văn này, tôi giả sử một mô hình chủ khách dựa trên hàng đợi công việc, mô hình này được dùng trong tất cả các hệ thống tính toán tình nguyện thực tế hiện nay, thêm vào đó là trong nhiều các hệ thống lưới, các hệ thống metacomputing, và toàn bộ các hệ thống tính toán song song dựa trên mạng diện rộng khác. Trong mô hình này một tính toán được chia vào thành vào một dãy các lô, mỗi lô bao gồm nhiều các đối tượng công việc độc lập nhau [1]. Tại thời điểm bắt đầu của mỗi lô, những đối tượng công việc này được đặt vào trong một hàng đợi công việc bởi nút chủ, và sau đó được phân phối đến các nút máy trạm đã đăng kí gia nhập vào máy tính tình nguyện để thực thi chúng song song và rồi trả về kết quả của chúng đến máy chủ khi chúng kết thúc nhiệm vụ tính toán. Khi máy chủ đã tập hợp được các kết quả cho tất cả các đối tượng công việc, nó sẽ tạo ra một lô các đối tượng công việc tiếp (có thể dùng dữ liệu từ các kết quả của lô hiện tại), đặt chúng vào trong hàng đợi công việc, và lập lại điều này cho toàn bộ xử lý. Trong mô hình này, tôi cũng giả sử rằng mọi nhiệm vụ có kích cỡ giống nhau.

Một giải thích cho mô hình này được chỉ đinh trong hình 2-1.

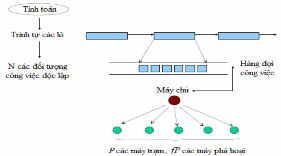
Hình 2-1. Mô hình chủ khách

Tỉ lệ lỗi. Chúng ta định nghĩa tỉ lệ lỗi, , là tỉ số của các kết quả lỗi hoặc các lỗi so với các kết quả cuối cùng được chấp nhận tại cuối của nhóm. Cách thứ hai, chúng ta cũng có thể định nghĩa nó là xác suất của từng kết quả cuối cùng riêng biệt là lỗi,

như vậy về trung bình, số lượng các lỗi được mong đợi trong một nhóm N các kết

quả được cho bởi . Để đơn giản, tôi giả sử rằng các nhóm công việc là độc lập lẫn nhau, do đó các lỗi trong một nhóm không ảnh hưởng lẫn nhau. Xa hơn, trong thiết kế các kĩ thuật của tôi, tôi giả sử rằng có một tỉ lệ lỗi chấp nhận được là khác

không, , và nhằm làm cho tỉ lệ lỗi thấp hơn nó. Một vài thuật toán “chịu lỗi tự

nhiên” như là các thuật toán di truyền, xuất video, và một vài các ứng dụng thống kê có thể cho phép có một phân số lớn liên quan (1% hoặc nhiều hơn) các kết quả cuối cùng là lỗi, và vì vậy có tỉ lệ lỗi chấp nhận cao. Trong các ứng dụng khác không cho phép bất cứ lỗi nào tại tất cả các kết quả, phải được thiết lập để làm

cho xác suất lấy được bất cứ nỗi nào tại tất cả các kết quả cuối cùng là tương đối nhỏ. Cho ví dụ, Giả sử rằng một tính toán có 10 lô mỗi lô có 100 đối tượng công việc riêng biệt và mỗi lô này phụ thuộc vào nhau do đó một kết quả lỗi trong bất cứ nhóm nào trong 10 lô sẽ là nguyên nhân của toàn bộ tính toán sai. Trong trường hợp này, để làm cho xác suất của toàn bộ tính toán là lỗi, P (lỗi), kém hơn 1%, tỉ lệ lỗi ,

tỉ lệ xác suất của một kết quả riêng biệt bị lỗi, phải không lớn hơn:

Kẻ phá hoại. Chúng ta giả sử rằng một phân số mắc lỗi, f, của toàn bộ máy trạm, P, là các kẻ phá hoại. Nút chủ (nút mà chúng ta giả sử là tin cậy) có thể không biết giá trị thực sự của f, nhưng được cho phép giả định một cận trên của nó, do đó không có sự đảm bảo cần được làm nếu phân số mắc lỗi thực lớn hơn cận trên giả định.

Để đơn giản, chúng ta giả định rằng tất cả các máy trạm, bao gồm cả các máy phá hoại, chạy chính xác với tốc độ giống nhau, để mà các đối tượng công việc là giống nhau và được phân bố ngẫu nhiên giữa các máy trạm và các máy phá hoại. Vì vậy, mỗi kết quả chúng ta nhận được là bằng giống như là đến từ bất cứ máy trạm nào, tỉ lệ lỗi gốc - nghĩa là tỉ lệ lỗi được mong đợi mà không phải chịu đựng lỗi đơn giản là f.

Tỉ lệ phá hoại và sự cấu kết. Cho đơn giản, chúng ta làm mỗi máy phá hoại theo phương thức Bernoulli với một xác suất s cho một kết quả lỗi, và chúng ta giả sử rằng s, được gọi là tỷ lệ phá hoại, là một hằng số theo thời gian và giống nhau cho tất cả các máy phá hoại.

Chú ý rằng trong giả sử này, các máy trạm và phá hoại là độc lập lẫn nhau và không giao tiếp với nhau. Đặc biệt, trong trường hợp ở đó các máy phá hoại không luôn cho kết quả sai, chúng ta giả sử rằng các máy phá hoại không tán thành cho kết quả sai, nhưng quyết định làm là độc lập.

Tuy nhiên, nếu hai hoặc nhiều máy phá hoại xuất hiện quyết định cho kết quả sai cho một thực thể công việc đặc biệt, chúng ta sẽ giả sử rằng các trả lời sai của chúng phù hợp, trừ trường hợp đã định khác. Điều này cho phép các máy phá hoại biểu quyết cùng nhau, và điều này không chỉ là một giả định có từ trực quan, chúng ta có thể mong đợi tỉ lệ lỗi cuối cùng thấp hơn nếu các máy phá hoại không thể biểu quyết cùng nhau.

Sự dư thừa và sự châm chễ. Thông thường, một kĩ thuật chịu lỗi mới đưa ra một vài thời gian tính toán thêm để thực thi lại các nhiệm vụ. Để đánh giá hiệu năng và hiệu quả của một kĩ thuật chịu lỗi, chúng ta quan tâm đến sự dư thừa và sự chậm chễ. Sự dư thừa được định nghĩa là tỉ số giữa số lượng tổng trung bình của các đối tượng công việc thực sự được gán đến các máy trạm trong một lô khi dùng kĩ thuật,

và số lượng gốc của các thực thể công việc, N. Sự chậm chễ được định nghĩa tương tự là tỉ số giữa các lần chạy của sự tính toán có và không có dùng kĩ thuật. Thông thường, sự dư thừa sẽ hướng tới một sự chậm chễ tương ứng, từ khi chúng ta giả sử rằng các đối tượng công việc nhiều hơn gấp nhiều lần các máy, để mà không có các máy trạm nhàn rỗi trong hầu hết các thời gian. Cho ví dụ, một kĩ thuật làm trung bình tất cả các công việc gấp hai lần sẽ mất thời gian gấp đôi.

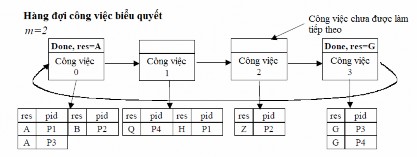
Hình 2-2. Hàng đợi công việc lập lịch tham lam với biểu quyết m đầu tiên

Tuy nhiên chú ý rằng, trong một vài trường hợp – đặc biệt khi máy trạm có thể gia nhập, dời đi hoặc cho vào danh sách đen trong giai đoạn giữa của lô – sự chậm chễ có thể khác so với sự dư thừa. Nếu máy trạm dời đi, cho ví dụ, thì các máy trạm còn lại phải lấy quá các công việc của chúng. Điều này tăng sự chậm chễ, thậm chí xuyên suất tổng số lượng của công việc, và vì vậy độ dư thừa là giống nhau.

2.2 Các kĩ thuật chịu lỗi truyền thống.

Thông thường, các kĩ thuật chịu lỗi nhằm vào (thứ tự ưu tiên): (1) tối thiểu tỉ lệ lỗi cuối cùng là nhỏ nhất có thể, hoặc giảm nó ít nhất đến một mức chấp nhận, (2) tối thiểu sự dư thừa, và (3) tối thiểu sự chậm chễ.

Cơ bản các kĩ thuật chịu lỗi dùng các kĩ thuật truyền thống như là biểu quyết, kiểm tra điểm hoặc danh sách đen để tăng độ tin cậy của các hệ thống tính toán tình nguyện. Trong kĩ thuật biểu quyết, mỗi nhiệm vụ được thực thi nhiều lần và kết quả tốt nhất được lựa chọn xuyên suốt một xử lý biểu quyết. Có hai cách biểu quyết: biểu quyết theo số đông và biểu quyết m đầu tiên. Trong cách biểu quyết đầu tiên, kết quả có số lượng biểu quyết giống nhau cao nhất được lựa chọn là kết quả cuối cùng, trong cách thứ hai, sự thực thi một nhiệm vụ được lập lại cho đến khi nút chủ

tập hợp đủ m kết quả giống nhau. Trong kĩ thuật kiểm tra điểm, máy chủ kiểm tra tính hợp lệ của máy trạm bằng cách cho ngẫu nhiên máy trạm một công việc được đánh dấu là kết quả chính xác đã thực sự được biết ở một nơi khác (ví dụ. Các công việc được đánh dấu đã được thực thi trên máy chủ hoặc trên một vài máy tính tình nguyện đáng tin cậy). Nếu kết quả trả về không đúng, nút chủ có thể từ bỏ kết quả hiện tại hoặc thậm chí quay lại kiểm tra lại tất cả các kết quả nhận được từ máy trạm đó. Trong trường hợp kĩ thuật danh sách đen, máy chủ có thể thêm các máy trạm nguy hiểm đã được dò tìm vào trong danh sách đen để ngăn chặn không cho chúng đệ trình các kết quả sai lại nhiều lần nữa.

2.2.1 Biểu quyết theo số đông

Chúng ta có thể dễ dàng thực thi giản đồ biểu quyết theo số đông truyền thống bằng cách dùng một hàng đợi công việc tham lam được thay đổi [11] được chỉ định trong hình 2-2. Ở đây, máy chủ tiếp tục đi xuyên suất các thực thể công việc trong hàng đợi công việc theo phương thức Rough-Robin, cho đến khi tất cả các cờ được làm của tất cả các thực thể công việc được thiết lập. Cờ được làm của mỗi thực thể công việc được dời không thiết lập cho đến khi chúng ta tập hợp được m kết quả phù hợp đầu tiên cho thực thể công việc đó, kết quả thực thi một giản đồ biểu quyết m đầu tiên. Giản đồ này có một sự dư thừa được mong đợi là , và một tỉ lệ lỗi giảm theo hàm mũ với m, được chỉ định trong hình 2-3 [8]. Tỉ lệ lỗi giảm theo hàm mũ nghĩa rằng các công việc được biểu quyết rất tốt trong các hệ thống với f nhỏ, và xa hơn, các công việc biểu quyết lấy tăng lên tốt hơn là f giảm. Vì vậy, trong hệ thống với tỉ lệ lỗi rất thấp để bắt đầu, như là hệ thống phần cứng, nó không lấy nhiều sự dư thừa để giảm tỉ lệ lỗi đến các mức vô cùng thấp.

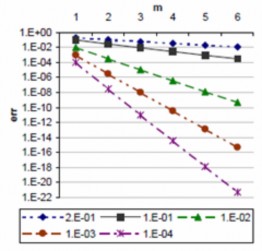
Hình 2-3. Tỉ lệ lỗi của biểu quyết số đông với nhiều các giá trị m và f [8]

Tuy nhiên biểu quyết cũng có các khó khăn của nó. Trước tiên nó không hiệu quả khi f không nhỏ. Được chỉ trong hình 2-3, cho ví dụ, tại f = 20%, làm tất cả các công việc ít nhất m = 6 lần vẫn còn một tỉ lệ lỗi lớn hơn 1%. Thứ hai và quan trọng hơn, nó có một sự dư thừa tối thiểu 2 ít liên quan đến f và tỉ lệ lỗi mục tiêu, . Vì

những lý do này biểu quyết chỉ được thực hiện thực tế trong các trường hợp ở đó:

(1) f là nhỏ (ví dụ, ) và (2) hoặc (a) chúng ta có đủ các nút nhàn rỗi hoặc dư thừa để lấy thêm công việc mà không là nguyên nhân tạo thêm sự chậm chễ hoặc

(b) sự chậm chễ của ít nhất hai (hoặc thông thường m) dường như là một cái giá chấp nhận được để trả cho việc giảm tỉ lệ lỗi.

2.2.2 Kiểm tra điểm

Trong trường hợp ở đó hoặc f là lớn, hoặc là tỉ lệ lỗi chấp nhận được lớn nhất của chúng ta là không quá nhỏ, chúng ta có thể sử dụng một lựa chọn mới gọi là kiểm tra điểm. Trong kiểm tra điểm, nút chủ không quay lại làm tất cả các đối tượng công việc hai hoặc nhiều lần, nhưng thay vào đó cho ngẫu nhiên một máy trạm một công việc giám sát, công việc mà kết quả đúng đã được biết trước hoặc sẽ được biết bằng việc kiểm tra nó trong một vài cách thức sau này.Sau đó nếu một máy trạm được bắt cho một kết quả tồi, máy chủ quay lại dò tất cả các kết quả nó đã nhận

được từ máy trạm đó và loại bỏ tất cả chúng. Máy chủ cũng có thể có danh sách đen máy phá hoại được bắt để mà ngăn chặn nó đệ trình các kết quả lỗi trong tương lai. Bởi vì kiểm tra điểm không bao gồm thực hiện lại tất cả các đối tượng công việc, nên nó có độ dư thừa thấp hơn nhiều với biểu quyết. Nếu chúng ta giả sử rằng máy chủ kiểm tra điểm mỗi máy trạm với một xác suất Bernoulli q, được gọi là tỉ lệ kiểm tra điểm, thì dư thừa, về trung bình, sẽ chỉ là . Cho ví dụ, nếu q = 10%, thì 10% của công việc máy chủ cho là công việc giám sát. Điều này có nghĩa rằng về trung bình, máy chủ cho ra bên ngoài các đối tượng công việc trong xuất tiến trình công việc của một lô với N các đối tượng công việc thực sự.

2.2.2.1Kiểm tra điểm dùng danh sách đen

Tuy nhiên, thậm chí với sự dư thừa thấp này, kiểm tra điểm có thể vẫn đạt được các tỉ lệ lỗi rất thấp. Xem điều này, quan tâm đến trường hợp ở đó các máy phá hoại bị bắt ở trong danh sách đen và không bao giờ cho phép quay trở lại hoặc tất cả các công việc nhiều hơn (ít nhất là trong lô hiện tại). Trong trường hợp này, các lỗi chỉ có thể đến từ các máy phá hoại mà tồn tại đến tận cuối của lô. Giả sử rằng một máy phá hoại được cho một tổng n đối tượng công việc, bao gồm cả các công việc giám sát, trong một lô. Ở đây n là phần được phân của máy phá hoại trong tổng công việc, ví dụ, N/P, thêm vào đó là sự dư thừa của kiểm tra điểm và tải thêm để mà các máy trạm duy trì lấy khi một máy trạm được lấy vào danh sách đen), vì vậy tỉ lệ lỗi cuối cùng trung bình với kiểm tra điểm có danh sách đen, , có thể

được tính là:

ở đây s là tỉ lệ lỗi của một máy giả mạo, f là phân số của toàn bộ máy gốc mà là các máy phá hoại, là xác suất của một máy phá hoại tồn tại trong xuất n vòng, và mẫu số biểu diễn phân số của toàn bộ máy trạm gốc tồn tại đến cuối cùng của lô, bao gồm đồng thời các máy trạm tốt và xấu. Phân tích kĩ hơn của hàm này