Application Algorithm To Expand Vietnamese Dictionary

The thesis builds a linked grammar dictionary consisting of over 40,000 entries based on the extended algorithm of [113] with a discriminant assessment based on the information in the Vietnamese dictionary.

2.2.1. Dictionary expansion algorithm

2.2.1.1 The idea of the algorithm

Szolovits [113] assumes that w is a word of the source vocabulary whose information is not known in the target vocabulary. If there is a word x in the source vocabulary that is indiscernible from w and if x has a lexical definition in the target vocabulary, then it makes sense to assign the definition of x to w.

The source vocabulary mentioned here is the words appearing in the UMLS Specialist Lexicon, while the target vocabulary is the LP (Link grammar Parser) vocabulary, which has the same structure as the thesis’s linked grammar dictionary. Two words in the source lexicon are indistinguishable if they have the same lexical description.

2.2.1.2. Mapping formalization

Assume W is the set of word meanings (words – words) in the source vocabulary and V is the set of word meanings in the target vocabulary.

For each w∈W, suppose Xw= { x | x is indistinguishable from w in the source vocabulary }. Define

Dw = { f(x) | x ∈ Xw, f(x) ≠ ⊥ } (Set of definitions in the target vocabulary of meanings that are not distinct from w in the source vocabulary).

The purpose of the algorithm is to relate w to one of the definitions of Dw. The problem is to choose the most appropriate definition in Dw.

Let I(d) = { v | f(v) = d } (the definition set in the target vocabulary shares the lexical description d).

For each d ∈ ef, calculate the number of common word meanings between I(d) and Xw and choose the definition for the largest intersection:

Figure 2.17. shows the diagram for the mapping algorithm according to [113].

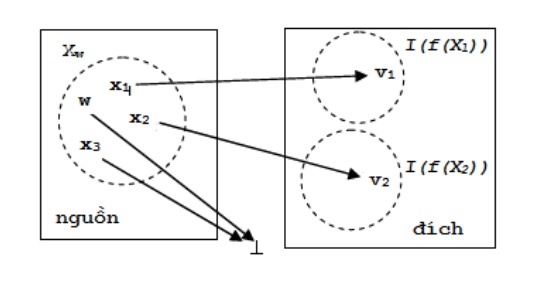
Figure 2.17. Intuitive mapping

2.2.2. Application algorithm to expand Vietnamese dictionary

With the limited information of the Vietnamese dictionary, the thesis also defines two meanings that are indistinguishable if and only if they have exactly the same lexical description as follows:

Same type of word (noun, verb…)
Same type of child
Have the same sentence pattern (with verbs)

Based on the intuitive method, the process of expanding the associative grammar dictionary is as follows:

Browse the Vietnamese dictionary data in turn. For each word find a set of words that are not distinct from it.
Find in that set of undifferentiated words the words that have been defined in the associated grammar dictionary data set and then give the formulas of those words.
Browse each formula in the current linked grammar dictionary, the formula with the largest number of words indistinguishable from the word to be defined, that formula is assigned to the word to be defined, and added. into grammar.

The use of heuristic algorithms to build dictionaries has given good results with basic word types: specific nouns, intransitive verbs, transitive verbs, and adjectives. For other word types, especially unclassified words (type “X”), manual repositioning is required. There are also a few other problems:

A word can be of many different word types. The solution of the thesis is to put each meaning in a different entry in the linked grammar dictionary. That will result in more analysis per sentence because the association analyzer misidentifies the formula. The de-ambiguity part of the thesis will deal with this problem.
The identification of words indistinguishable down to the subcategory causes errors with sub-types such as “had”, “is” because in the Vietnamese dictionary, they are placed in the same category, but in the linking language dictionary, two words which are of two different subcategories.
Like [111], the analyzer ignores the prepositions, for example “a ha”, “a so that”

Once the “raw” dictionary is obtained, manual correction is done to produce a complete associative grammar dictionary.

2.2. Conclude

In summary, to build the dictionary, the thesis has done through the main stages:

1. Building Linking Formulas

Research the English linking dictionary, find the linking formulas that can be used for Vietnamese and add to the linked dictionary.
Research Vietnamese grammar and French words to build linking formulas for some typical words.

2. Assign the linking formula to the word

Review sample text, word by word. Look up the linked dictionary to find if the word in question already corresponds to a linked formula, if not, manually add new words and formulas to the dictionary.
Browse the Vietnamese dictionary, assign each word to a formula in the dictionary according to Szolovits’ algorithm with the definition of undifferentiated words for Vietnamese. The process of building a dictionary can be depicted in Figure 2.18.
The process of building a Vietnamese linked grammar dictionary is depicted in Figure 2.18.

After the process of building and testing, the thesis has built a grammar dictionary linked with over 150 large formulas (each large formula includes one or more sub-formulas linked together via the or or xor) and 77 types of connections for all types of words in Vietnamese. To get this dictionary, the thesis has summarized from many documents on Vietnamese grammar, referring to how to build dictionaries for use on computers by many research groups: VLSP, Ho Ngoc Duc, Vdict… The thesis’s dictionary has met the requirement of analyzing basic structures and some common exceptions of Vietnamese.

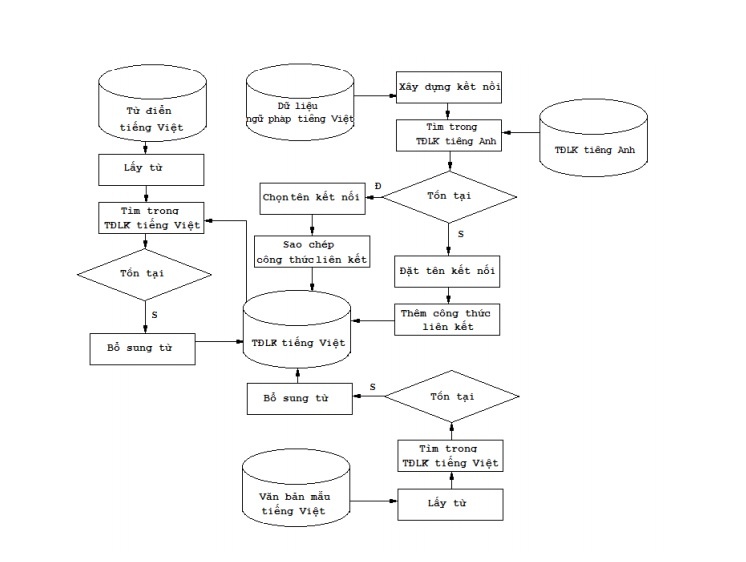
Figure 2.18. The process of building a Vietnamese linking grammar dictionary

Because it was built in a short time (2009 – 2012), there are many exceptions of Vietnamese that the dictionary cannot cover. Compared with the number of over 1000 large formulas of the English linked dictionary after 21 years (1991 – 2012) of continuously updating exceptions, the number of formulas of the Vietnamese linked dictionary is still small. To develop into a full dictionary, it is certainly necessary to test the analyzer with a very large corpus and support from linguists.

CHAPTER 3

ANALYSIS ON LINKED PHARMACOLOGY

3.1. Link Parser

3.1.1. Parsing Algorithm

The algorithm for analyzing sentences in the associative grammar was proposed by [111] based on the dynamic programming method. The algorithm seeks to build a top-down association analysis that meets the criteria outlined in the previous chapter.

Initially, the purpose of the algorithm is to find a link between the first word (from the 0th word) and the last word (from the nth word). Actually the words in the sentence are numbered from 0 to n-1. The nth word is a “virtual” word with the form (NIL)(NIL).

A collection d of some word will have pointers to two lists of connections. These pointers are denoted by left[d] and right[d]. If c is a connection, then next[c] denotes the next connection after c in its list. The next field of the last pointer in the list is equal to NIL. Figure 3.1 below shows the operation of the analyzer after considering the connection l’ on the word L and the connection r’ on the word R. l is next[l’] and r is next[r’].

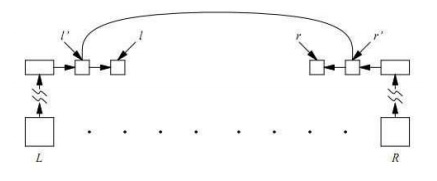
Figure 3.1. Analytical Algorithm

The extension of the local solution to the region between L and R is done by considering the words W in the range between L and R respectively, depicted in Figure 3.2 below.

Figure 3.2. Local solution

Below is the parsing algorithm of [111]. The COUNT function gives the total number of possible connections.

PARSE
t ← 0
for each d form of the word 0
do if left [d] = NIL
then t ← t + COUNT(0, n, right [d], NIL)
return t

Maybe you are interested!

Figure 3.3. Link Parsing Algorithm

The COUNT[111] function is described as shown in Figure 3.4. below:

COUNT(L, R, l, r)
if L = R + 1
then if l = NIL and r = NIL
then return 1
else return 0
else total ← 0
for W ← L + 1 to R – 1
do for each d form of the word W
do if l ≠ NIL and left[d] ≠ NIL and MATCH(l,left[d])
then leftcount ← COUNT(L, W, next[l], next[left[d]])
else leftcount ← 0
if right[d] ≠ NIL and r ≠ NIL and MATCH(right[d],r))
then rightcount ← COUNT(W, R, next[right[d], next[r])
else rightcount ← 0
total ← total + leftcount * rightcount
if leftcount > 0
then total ← total + leftcount *COUNT(W, R, right[d], r)
if (rightcount > 0 and l = NIL
then total ← total + rightcount * COUNT(L, W, l, left[d])
return total

Figure 3.4.COUNT function for the analysis number of the sentence.