Trọng Lượng Và Giá Trị Của 4 Loại Đồ Vật

	1	2		3	4	5
1		0		2	0	0	6
2	0			2	8	1	4
3	11	2			0	3	5
4	0	0		0		8	6
5	10	3		10	0		5
		1		3		2

Có thể bạn quan tâm!

• Thiết kế và đánh giá thuật toán - 14
• Thiết kế và đánh giá thuật toán - 15
• Thiết kế và đánh giá thuật toán - 16
• Thiết kế và đánh giá thuật toán - 18
• Quy Tắc Tam Giác Pascal O(N,k) Chính Là Comb(N,k) Và Ta Có Giải Thuật Như Sau:
• Trọng Lương Và Giá Trị 5 Loại Đồ Vật

Xem toàn bộ 205 trang tài liệu này.

C =

Tổng các hằng số rút gọn: 6 + 4 + 5 + 6 + 5 + 1 + 3 + 2 = 32. Đây là cận dưới của mọi hành trình.

* Chọn cạnh phân nhánh

Ta có số 0 ở hàng 5 cột 4 là số 0 mà khi thay bằng  sẽ cho tổng các hằng số rút gọn là lớn nhất. Do đó ta sẽ chọn cạnh (5, 4) để phân nhánh.

- Nhánh gồm các hành trình không chứa cạnh (5, 4)

Với nhánh này ta thay số 0 ở hàng 5 cột 4 bằng  rồi rút gọn ma trận thì ta được ma trận rút gọn là:

1	2	3	4	5
1		0	2	0	0
2	0		2	8	1
3	11	2		0	3
4	0	0	0		8
5	7	0	7		

Cận dưới của nhánh là 35

- Nhánh gồm các hành trình có chứa cạnh (5, 4)

Với nhánh này ta xoá khỏi ma trận rút gọn hàng 5 cột 4, thay giá trị ở hàng 4 cột 5 bằng  (ngăn cấm việc tạo thành hành trình con) và rút gọn ma trận, cụ thể bớt mỗi phần tử ở hàng 3 một lượng là 2. Ta được ma trận rút gọn của nhánh này và cận dưới của nhánh là 34.

3

5
1		0	2	0
2	0		2	1
3	9	0		1
4	0	0	0	

1 2

Với nhánh này ta lặp lại việc chọn cạnh phân nhánh. Cụ thể, ta chọn cạnh (4, 3) để phân nhánh.

- Với nhánh không chứa cạnh (4, 3) ta thay số 0 ở hàng 4 cột 3 bằng  rồi rút gọn ma trận ta được cận dưới của nhánh là 36 và ma trận rút gọn của nhánh là:

1	2	3	5
1		0	0	0
2	0		0	1
3	9	0		1
4	0	0		

- Với nhánh có chứa cạnh (4, 3) ta xoá khỏi ma trận hàng 4 cột 3, thay giá trị ở hàng 3 cột 5 bằng  (ngăn cấm việc tạo thành hành trình con) ta được ma trận rút gọn của nhánh và cận dưới của nhánh là 34

1	2	5
1		0	0
2	0		1
3	9	0	

- Với nhánh này ta lặp lại việc chọn cạnh phân nhánh. Cụ thể ta chọn cạnh (2, 1) để phân nhánh.

- Với nhánh không chứa cạnh (2, 1) ta thay số 0 ở hàng 2 cột 1 bằng  rồi rút gọn ma trận ta được cận dưới của nhánh là 44 và ma trận rút gọn của nhánh là:

1	2	5
1		0	0
2			0
3	0	0	

- Với nhánh có chứa cạnh (2, 1) ta xoá khỏi ma trận hàng 2 cột 1, thay các giá trị ở hàng 3 cột 5 và hàng1 cột 2 bằng  (ngăn cấm việc tạo thành hành trình con) ta được ma trận rút gọn của nhánh và cận dưới của nhánh là 34

2	5
1		0
3	0	

Đến đây ta bổ sung thêm hai cạnh ứng với hai số 0 trong ma trận rút gọn trên ta được một hành trình đầy đủ gồm các cạnh:

(5, 4); (4, 3); (2, 1); (1, 5); (3, 2)

Chi phí của hành trình này là: 5 + 9 + 4 + 8 + 8 = 34. Quá trình trên được mô tả như sau:

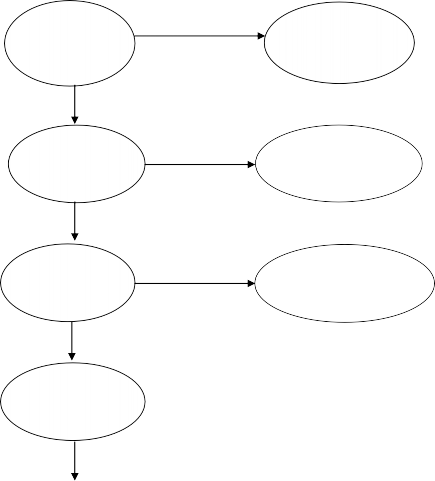
Tập tất cả các hành trình

Cận dưới = 32

Tập hành trình không chứa (5, 4)

Cận dưới = 35

Tập các hành trình chứa (5, 4)

Cận dưới = 34

Tập các hành trình không chứa (4,3)

Cận dưới = 36

Tập các hành trình chứa (4,3)

Cận dưới = 34

Tập các hành trình không chứa

(2,1)

Cận dưới = 44

Tập các hành trình chứa (2,1)

Cận dưới =34

Ta được một hành trình gồm các cạnh:

(5, 4); (4, 3); (2, 1); (1, 5); (3, 2) có chi phí 34

Hình 5.3. Quá trình phân nhánh

Ta thấy tất cả các nhánh còn lại đều có cận dưới lớn hơn 34, do đó không cần phải phát triển tiếp nữa và khẳng định hành trình tìm được ở trên là hành trình tối ưu.

5.2.2. Bµi to¸n chiÒc ba l«

1) Bµi to¸n

Cho một cái ba lô có thể đựng một trọng lượng m và n loại đồ vật. Đồ vật i có trọng lượng wi và giá trị vi. Tất cả các loại đồ vật đều có số lượng không hạn chế. Tìm một cách lựa chọn các đồ vật đựng vào ba lô sao cho tổng trọng lượng không vượt quá m và tổng giá trị là lớn nhất. (Với giả thiết m, wi, vi là các số nguyên)

Phân tích bài toán:

Ký hiệu tập các số nguyên không âm là Z*

Đặt : D = {x=(x1, x2, ..., xn): xi Z* và

n

xi wi

i1

m }

Thì D là tập các phương án. Ta xây dựng hàm f(x) với xD như sau:

n

f(x)= xi vi

i1

Khi đó bài toán chiếc ba lô chuyển về bài toán sau : Tìm x*  D : f* = f(x*) =max { f(x ): xD}

Ta sẽ kết hợp đánh giá nhánh cận trong quá trình liệt kê các lời giải theo kỹ thuật quay lui.

2) Thiết kế thuật toán

Mô hình ban đầu có thể sử dụng như sau : Try(i)

{

for(j = 1 ? t)

if(Chấp nhận j)

{

Xác định xi theo j; Ghi nhận trạng thái; if(i==n)

else

{

}

Cập nhật lời giải tối ưu;

Xác định cận trên g; if( g(x1,..., xi) ≤ f*) Try(i+1);

Hoàn trả trạng thái;

}

}

- Cách chọn vật :

Đánh số các loại đồ vật từ 1 đến n.

vi

w

Tính đơn giá cho các loại đồ vật dgi =

i

i=1, 2,..., n

Sắp xếp vật theo thứ tự giảm dần của đơn giá và chọn vật theo thứ tự này.

- Đánh giá cận trên :

Giả sử đã tìm được lời giải bộ phận : (x1 , x2, ..., xk ) . Khi đó :

k

+ Giá trị của các đồ vật trong ba lô sẽ là : S = xi vi

i1

+ Tổng trọng lượng các vật đã được xếp vào ba lô là :

k

T = xi wi

i1

k

+ Trọng lượng còn lại của ba lô là : mi = m – T = m - xi wi

i1

Giả sử ta có phương án bộ phận cấp i: (u1, u2, ..., ui) khi đó ta có: max{f(x): x=(x1, x2, ..., xn)D; xj=uj j=1, 2, ..., i }

n

= max{S + x j v j :

ji1

n

x j wj ji1

mi }

n

= S + max{ x j v j :

ji1

n

x j wj ji1

mi }  S + vi+1[ mi ]

wi

( [ mi ] là phần nguyên của

wi

mi )

wi

Do đó cận trên cho phương án bộ phân cấp i có thể được xác định là:

g(u1, u2, ..., ui) = S + vi+1[ mi ]

wi

- Các giá trị có thể chấp nhận được cho xi+1 là:

j = 0 -> [ mi ]

wi

- Ghi nhận trạng thái khi xác định xi:

+ Cập nhật tổng giá trị các vật trong ba lô: S = S + xivi

+ Cập nhật trọng lượng còn lại của ba lô: T = T - xiwi

- Hoàn trả trạng thái :

+ S = S - xivi

+ T = T + xiwi

- Cập nhật lời giải tối ưu :

Khi tìm được một lời giải, ta so sánh lời giải này với lời giải mà ta coi là tốt nhất đang có để chọn lời giải tối ưu.

• Các khởi tạo giá trị ban đầu :

+ x* = 0 ;//Lời giải tối ưu của bài toán

+ f* = f(x*) = 0;// Giá trị tối ưu

+ S = 0;//Giá trị thu được từng bước của ba lô.

+ T =0 ;//Trọng lượng xếp vào ba lô từng bước.

Hàm tr(y) sẽ được làm mịn hơn như sau: input:

m, n

v=(v1, . . ., vn)

w=(w1,..., wn ) Output:

x* = (x1,..., xn)

f* = f(x*) =max { f(x ): xD} Try(i)

{

t = (m-T)/wi ;

for (j = t; j >=0 ; j--)

{

xi = j;

// Ghi nhan trang thai T = T + wi*xi ;

S = S + xi*vi;

if(i==n)//Cap nhat toi uu

{

if(S > f*)

{

x* = x; f* = S;

}

}

else

{

g = S + vi+1*(m-T)/wi+1; //Danh gia can if ( g > f*)

Try(i+1);

}

// Hoan tra trang thai T = T – wi*xi;

S = S - vi*xi;

}

}

Ví dụ 5.3.

Giải bài toán chiếc ba lô với chiếc ba lô có thể đựng được trọng lượng m = 8, có 4 loại đồ vật với trọng lượng và giá trị của từng loại như sau:

Đồ vật

1	2	3	4
Trọng lượng	5	3	2	4
Giá trị	10	5	3	6

Hình 5.4. Trọng lượng và giá trị của 4 loại đồ vật

x2=1

x2=0

Quá trình giải bài toán trên theo thuật toán nhánh cận được mô tả trong cây tìm kiếm sau:

f* = 0

x1=1

x1=0

(1):S=10; T=5; g=15;

(1):S=0; T=0; g=10;

(1,0):S=10; T=5; g=13;

x3=0

x4=0

(1,1):S=15; T=8; g=15;

(1,1,0):S=15 T=8; g=15;

C¸c nh¸nh nµy bÞ lo¹i v× cã cËn d•íi g < f*= 15

(1,1,0,0): S=15;T=8;

x*= (1,2,3,4,5)

f*=15

Hình 5.5. Cây tìm kiếm

Xem tất cả 205 trang.