Trang 16
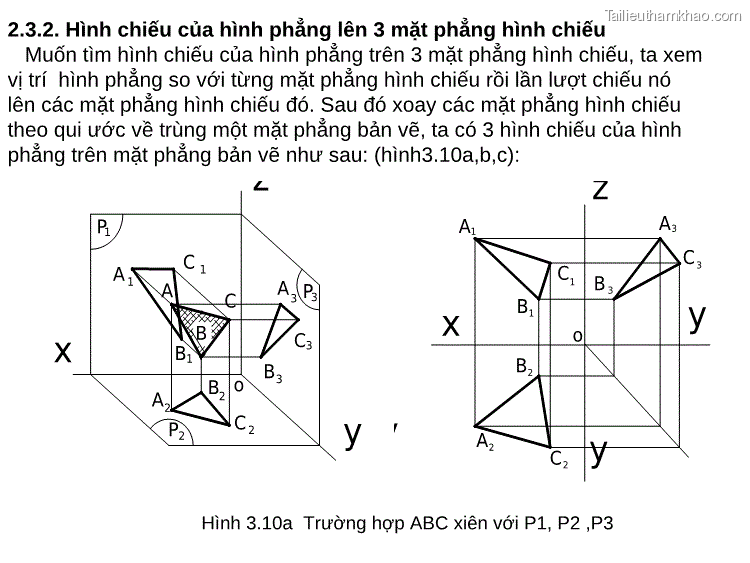
2.3.2. Hình chiếu của hình phẳng lên 3 mặt phẳng hình chiếu Muốn tìm hình chiếu của hình phẳng trên 3 mặt phẳng hình chiếu, ta xem vị trí hình phẳng so với từng mặt phẳng hình chiếu rồi lần lượt chiếu nó lên các mặt phẳng hình chiếu đó. Sau đó xoay các mặt phẳng hình chiếu theo qui ước về trùng một mặt phẳng bản vẽ, ta có 3 hình chiếu của hình phẳng trên mặt phẳng bản vẽ như sau: (hình3.10a,b,c): P1 A C 1 1 A C A 3 P 3 B B1 C3 A2 P2 B 2 o C 2 B3 A1 A3 C3 B 3 x B1 y B2 A2 C 2 y C1 o z x y Hình 3.10a Trường hợp ABC xiên với P1, P2 ,P3
Có thể bạn quan tâm!
Trang 17
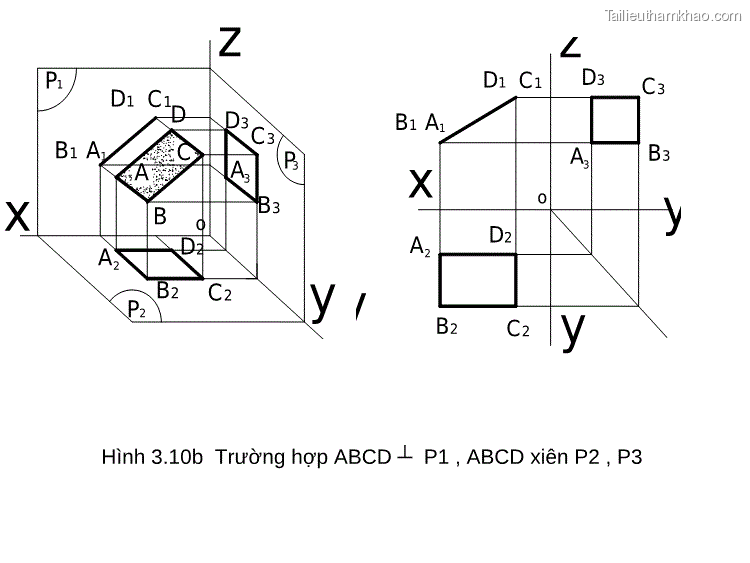
P z 1 D D1 C1D 3C3 B1 A1 z D1 C1 D3 C3 C B1 A1 x B3 o A3 P3 x A A3 D2 B o B3 y A A D2 y 2 P B2 C2 2 2 B2 C2 y Hình 3.10b Trường hợp ABCD ┴ P1 , ABCD xiên P2 , P3
Trang 18
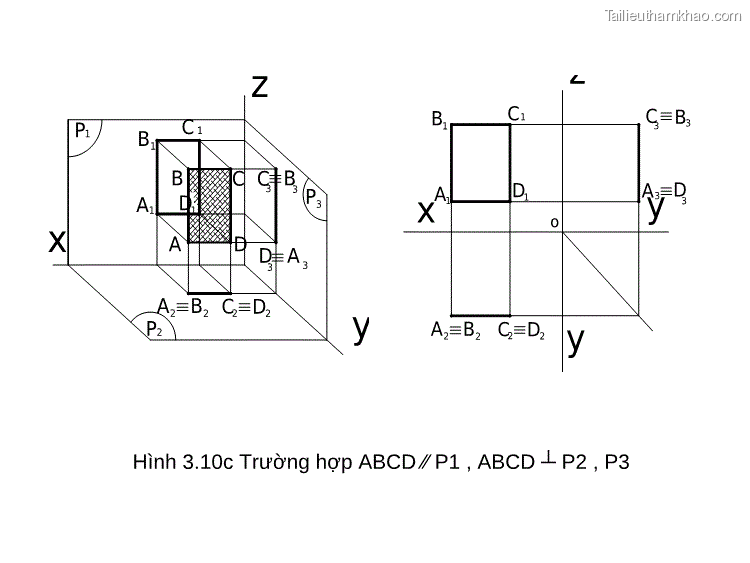
B P1 C 1 1 B A D z B1 C1 C 3 xA1 D1 Ay3 A2 B2 C2 D2 y o B3 3 3 C C B P D A 1 1 3 3 D D A x 3 3 A2 B2 C2 D2 P2 y Hình 3.10c Trường hợp ABCD ⁄⁄ P1 , ABCD ┴ P2 , P3
Trang 19
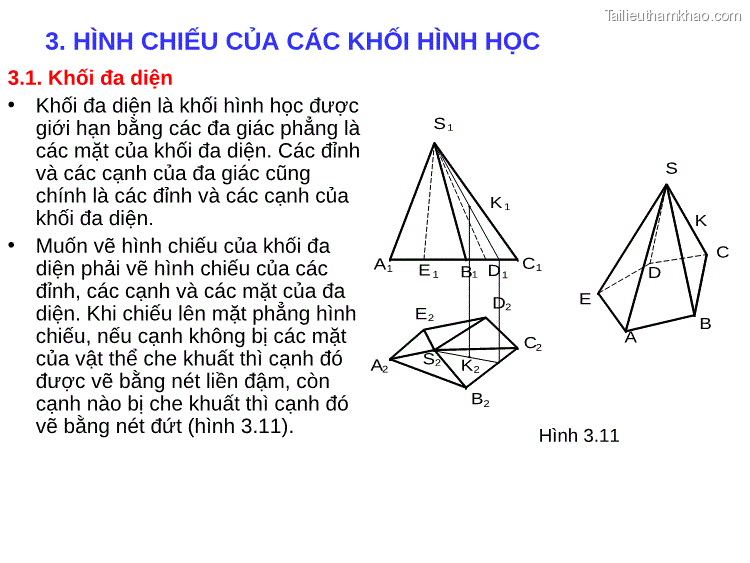
3. HÌNH CHIẾU CỦA CÁC KHỐI HÌNH HỌC 3.1. Khối đa diện • Khối đa diện là khối hình học được giới hạn bằng các đa giác phẳng là các mặt của khối đa diện. Các đỉnh và các cạnh của đa giác cũng chính là các đỉnh và các cạnh của khối đa diện. • Muốn vẽ hình chiếu của khối đa diện phải vẽ hình chiếu của các A1 đỉnh, các cạnh và các mặt của đa diện. Khi chiếu lên mặt phẳng hình chiếu, nếu cạnh không bị các mặt của vật thể che khuất thì cạnh đó A2 được vẽ bằng nét liền đậm, còn cạnh nào bị che khuất thì cạnh đó vẽ bằng nét đứt (hình 3.11). S1 K D B S K 1 C E 1 B1 D1 C1 D2 E E2 C2 A S2 K2 B2 Hình 3.11
Trang 20
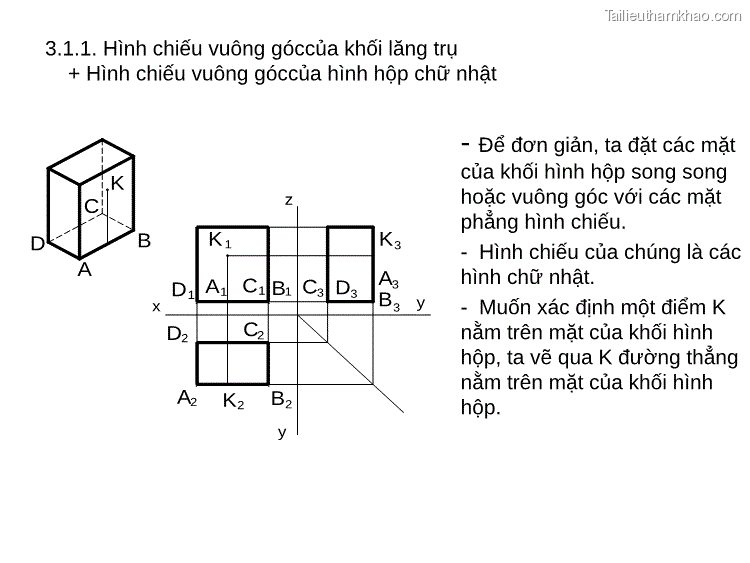
3.1.1. Hình chiếu vuông góccủa khối lăng trụ + Hình chiếu vuông góccủa hình hộp chữ nhật K C z K 1 D1 A1 K3 A3 B3 y D2 A2 K2 B2 y C1 B1 C3 D3 C2 - Để đơn giản, ta đặt các mặt của khối hình hộp song song hoặc vuông góc với các mặt phẳng hình chiếu. D B - Hình chiếu của chúng là các A hình chữ nhật. x - Muốn xác định một điểm K nằm trên mặt của khối hình hộp, ta vẽ qua K đường thẳng nằm trên mặt của khối hình hộp.
Trang 21
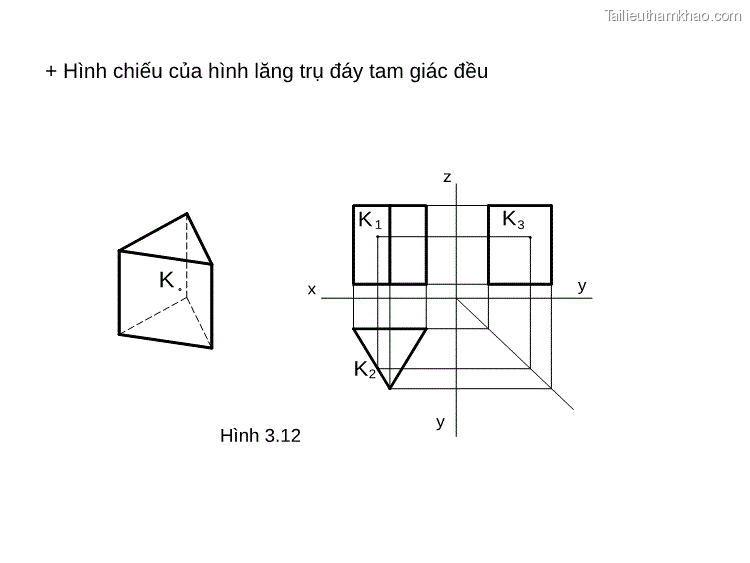
+ Hình chiếu của hình lăng trụ đáy tam giác đều K 1 K3 y K2 y z K x Hình 3.12
Trang 22
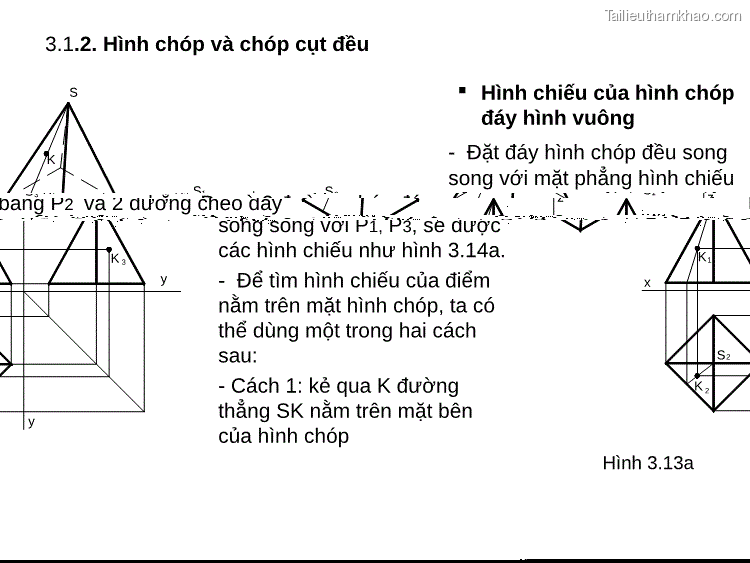
3.1 .2. Hình chóp và chóp cụt đều S1 z S3 K 3 x y K 2 y K1 S2 S K Hình 3.13a Hình chiếu của hình chóp đáy hình vuông - Đặt đáy hình chóp đều song song với mặt phẳng hình chiếu bằng P2 và 2 đường chéo đáy song song với P1, P3, sẽ được các hình chiếu như hình 3.14a. - Để tìm hình chiếu của điểm nằm trên mặt hình chóp, ta có thể dùng một trong hai cách sau: - Cách 1: kẻ qua K đường thẳng SK nằm trên mặt bên của hình chóp
Trang 23
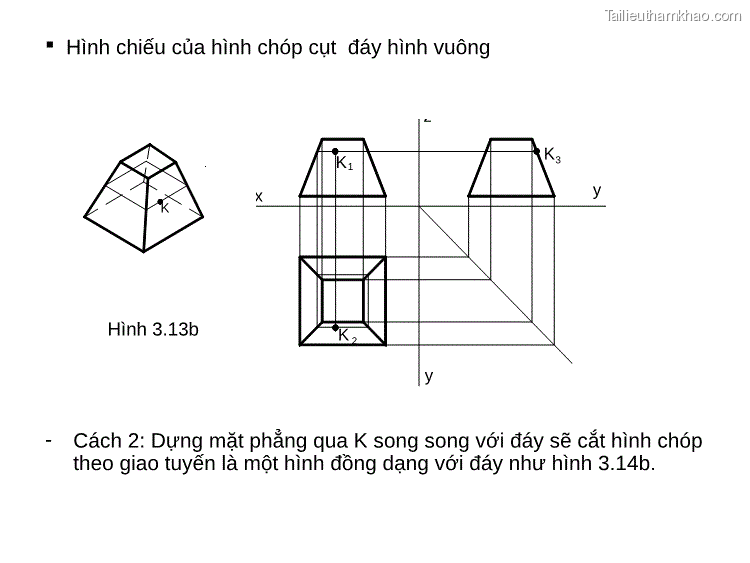
Hình chiếu của hình chóp cụt đáy hình vuông K K3 x y K 2 y K1 Hình 3.13b - Cách 2: Dựng mặt phẳng qua K song song với đáy sẽ cắt hình chóp theo giao tuyến là một hình đồng dạng với đáy như hình 3.14b.

Trang 24
3.2. Khối tròn xoay Hình 3.15 • Khối tròn xoay là khối hình học giới hạn bởi mặt tròn xoay hay một phần mặt tròn xoay và các mặt phẳng. • Mặt tròn xoay là mặt tạo bởi một đường bất kỳ quay một vòng quanh một đường thẳng cố định. Đường bất kỳ gọi là đường sinh của mặt tròn xoay, đường thẳng cố định gọi là trục quay của mặt tròn xoay. Mỗi điểm của đường sinh khi quay sẽ tạo thành một đường tròn có tâm nằm trên trục quay và bán kính bằng khoảng cách từ điểm đó đến trục quay (hình 3.15). - Nếu đường sinh là đường thẳng song song trục quay sẽ tạo thành mặt trụ tròn xoay. - Nếu đường sinh là đường thẳng cắt trục quay sẽ tạo thành mặt nón tròn xoay - Nếu đường sinh là nửa đường tròn quay quanh trục quay là đường kính của nó sẽ tạo thành mặt cầu tròn xoay.
Trang 25
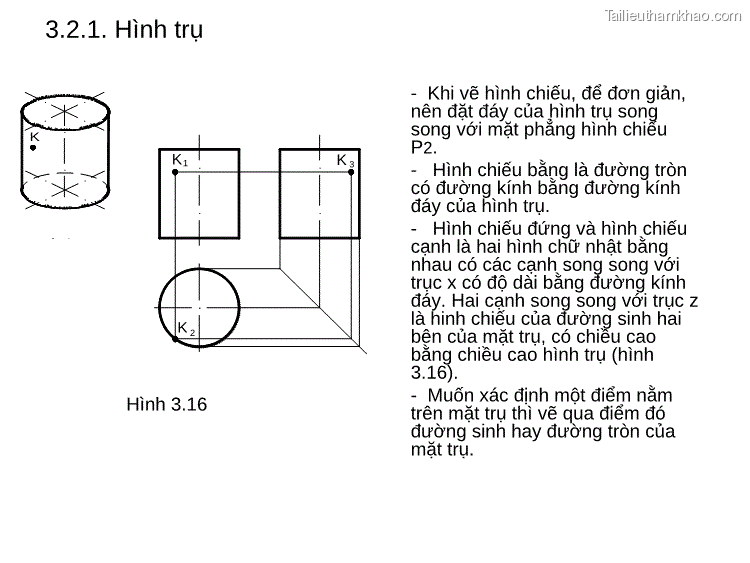
3.2.1. Hình trụ K Hình 3.16 - Khi vẽ hình chiếu, để đơn giản, nên đặt đáy của hình trụ song song với mặt phẳng hình chiếu P2. K1 K 3 K 2 - Hình chiếu bằng là đường tròn có đường kính bằng đường kính đáy của hình trụ. - Hình chiếu đứng và hình chiếu cạnh là hai hình chữ nhật bằng nhau có các cạnh song song với trục x có độ dài bằng đường kính đáy. Hai cạnh song song với trục z là hinh chiếu của đường sinh hai bên của mặt trụ, có chiều cao bằng chiều cao hình trụ (hình 3.16). - Muốn xác định một điểm nằm trên mặt trụ thì vẽ qua điểm đó đường sinh hay đường tròn của mặt trụ.
Trang 26
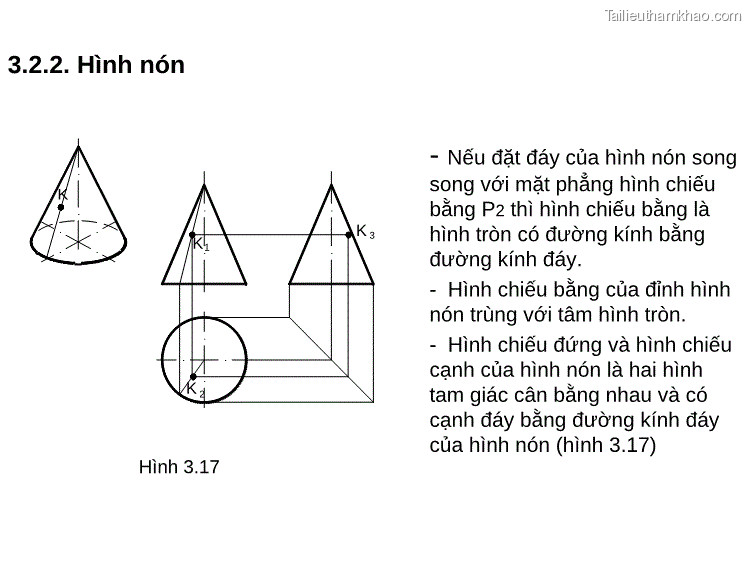
3.2.2. Hình nón K Hình 3.17 - Nếu đặt đáy của hình nón song song với mặt phẳng hình chiếu bằng P2 thì hình chiếu bằng là hình tròn có đường kính bằng đường kính đáy. K1 K 3 K 2 - Hình chiếu bằng của đỉnh hình nón trùng với tâm hình tròn. - Hình chiếu đứng và hình chiếu cạnh của hình nón là hai hình tam giác cân bằng nhau và có cạnh đáy bằng đường kính đáy của hình nón (hình 3.17)
Trang 27
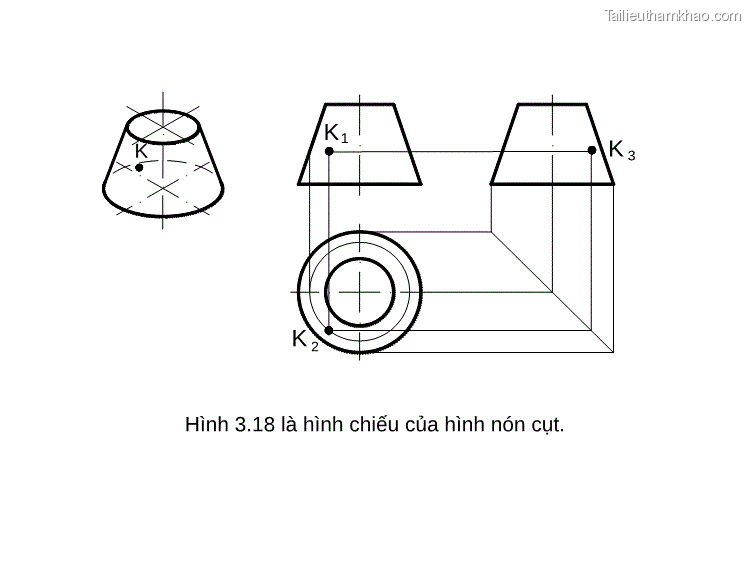
K K1 K 3 K 2 Hình 3.18 là hình chiếu của hình nón cụt.
Trang 28
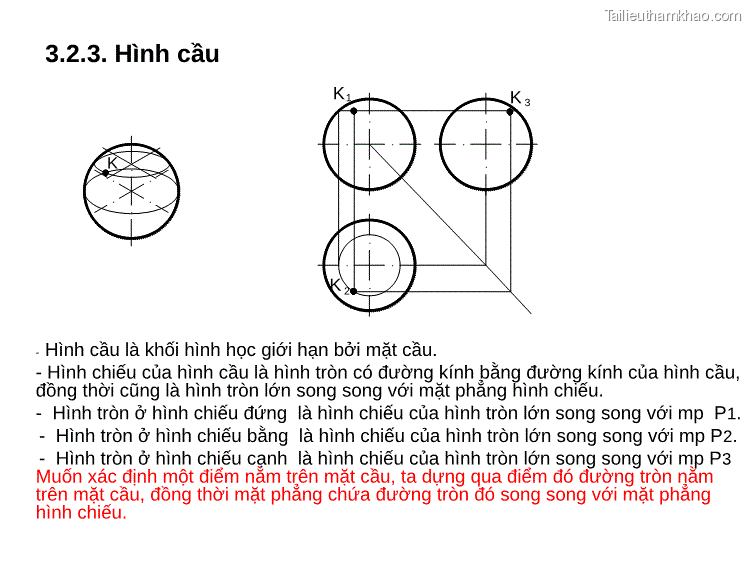
3.2.3. Hình cầu K K1 K 3 K 2 - Hình cầu là khối hình học giới hạn bởi mặt cầu. - Hình chiếu của hình cầu là hình tròn có đường kính bằng đường kính của hình cầu, đồng thời cũng là hình tròn lớn song song với mặt phẳng hình chiếu. - Hình tròn ở hình chiếu đứng là hình chiếu của hình tròn lớn song song với mp P1. - Hình tròn ở hình chiếu bằng là hình chiếu của hình tròn lớn song song với mp P2. - Hình tròn ở hình chiếu cạnh là hình chiếu của hình tròn lớn song song với mp P3 Muốn xác định một điểm nằm trên mặt cầu, ta dựng qua điểm đó đường tròn nằm trên mặt cầu, đồng thời mặt phẳng chứa đường tròn đó song song với mặt phẳng hình chiếu.
Trang 29
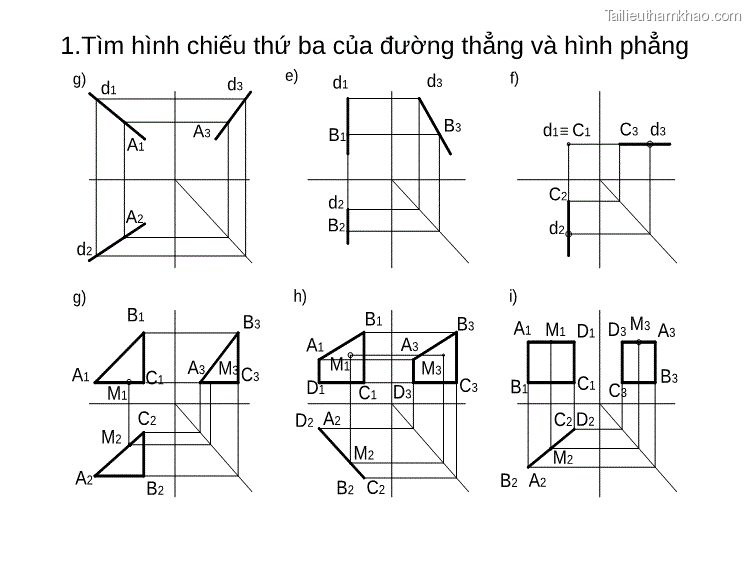
1.Tìm hình chiếu thứ ba của đường thẳng và hình phẳng g) d1 d3 e) d1 d3 f) d2 A1 A3 A2 B1 B3 d2 B2 d1 C1 C3 d3 C2 d2 g) h) i) B1 B3 A1 A3 D1 M3 C3 D2 A2 B2 C2 M1 C1 D3 M2 A1 M1 D1 D3 M3 A3 B1 C1 C B3 C2 M2 2 A2 3 D2 C1 A3 M3 B1 B3 A1 C3 M1 C2 M2 A2 B2 B
Trang 30
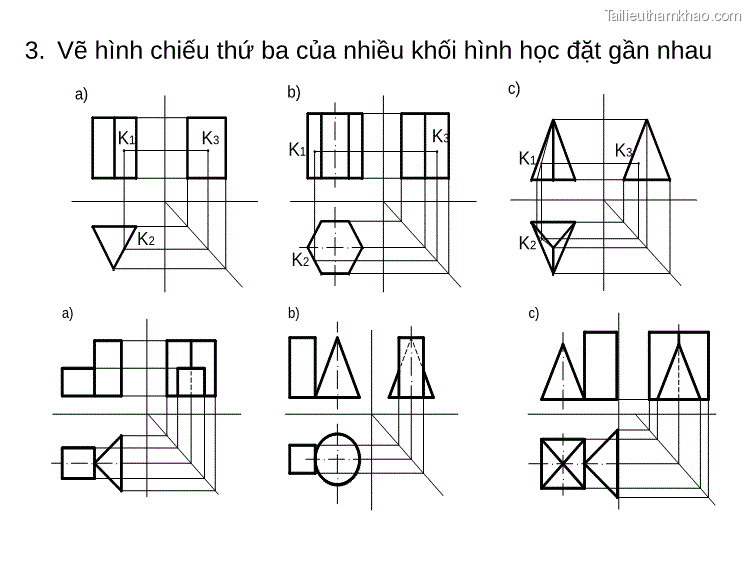
3. Vẽ hình chiếu thứ ba của nhiều khối hình học đặt gần nhau K1 K3 K2 K1 K3 K2 K1 K3 K2 a) b) c) a) b) c)