Data Processing Results of Sample Using Short Fiber Type (Lf/df=63.63)

From the experimental results of determining the splitting tensile strength (f sp ) of 105 standard concrete cylinders of 70MPa grade, for two types of short and long fibers, the analysis gives the correlation function between the splitting compressive strength and the steel fiber content. Using the univariate linear regression method and Minitab V17 statistical analysis software to find the relationship between the splitting compressive strength ( f sp ) and the fiber content (V f ).

The regression results found coefficients A and B for two cases of steel fiber reinforcement, short fiber (L f /D f = 63.63) and long fiber (L f /D f = 80) shown in Figure 2.32 and Figure 2.33. The equations with large correlation coefficients r 2 are r 2 = 86.3% (short fiber type), r 2

f sp =5.426+2.950V f

Splitting compressive strength (f sp ,MPa)

= 86.0% (long fiber type) and these values are all greater than 80%. This shows that the regression models are suitable and statistically significant.

f sp =5.813+3.755V f

Splitting compressive strength (f sp ,MPa)

Figure 2.32. Data processing results of the sample using short fibers (l f /d f =63.63)

Figure 2.33. Data processing results of the sample using long fibers (L f /D f =80)

f '

From the above experimental results, we have the coefficients A=5.426 and B=2.95 for the short fiber case (L f /D f =63.63) and the coefficients A=5.813 and B=3.755 for the long fiber case.

(L f /D f =80). If we leave it in the form A= a

and B= b (L f /D f)

then with concrete level

f' c = 70MPa, in both cases above, the values of coefficients a, b are the same (a=0.6); b=0.55). Therefore, the thesis provides a model for calculating the splitting compressive strength of high-strength concrete reinforced with steel fibers ( f sp ) as equation (2-79) for both short and long fibers.

f  0.6 f '  0.55 f V f '

sp c d fc

(2-78)

Maybe you are interested!

Thus, the tensile contribution of concrete is as equation (2-79).

 0.6 '

sp c

(2-79)

Therefore, the contribution of steel fiber reinforcement to the split compressive strength of steel fiber reinforced concrete is as follows:

 L f V f

spf d fc

0.55 '

(2-80)

The direct tensile strength and split compressive strength of CST concrete proposed in ACI 544-4R88 standard [32] have the following relationship:

 2 / 3

product

(2-81)

Therefore, formula (2-80) is multiplied by a factor of 2/3, the result of calculating the contribution of steel fiber reinforcement to the axial tensile strength of reinforced concrete is as equation (2-82)

 L f V f

f D fc

0.37 '

(2-82)

2.3.3. Proposed shear strength calculation model of CST reinforced concrete beams and problem block diagram

 Model for calculating shear resistance of reinforced concrete beams CST:

From the experimental results of determining the residual tensile strength (after cracking) of CĐCCST concrete as in equation (2-82), substitute this equation into (2-68) and (2-69), the argument is

The project gives the formula to predict the shear strength of CST reinforced concrete beams as (2-83). To consider the influence of beam effects and arch effects if the ratio a/d < 2.5, the formula is multiplied by 2.5d/a as in equation (2-84). From there, the shear strength for this type of beam can be calculated as (2-85) and (2-86).

V  f  V L f f  f , when a/d ≥ 2. 5

ncf D cz szcr f

' 0.37' cotton

(2-83)

V  2.5 d / a ( f '  0.37 V L f f ' cot  f cot ) , when a/d < 2.5;

ncf D cz szcr f

(2-84)

V  ( f '  0.37 V L f f ' cot  f cot ) bd , when a/d ≥ 2. 5

ncf D cz szcr etc

(2-85)

V  2.5 d / a ( f '  0.37 V L f f ' cot  f cot ) bd ,when a/d < 2.5;

ncf D cz szcr etc

(2-86)

Calculations based on the model proposed by the thesis can easily predict shear strength without the need for experimental data like some models proposed in international standards. It is completely possible to predict the crack angle and deformation in longitudinal reinforcement in reinforced concrete beams. It is possible to fully investigate the influence of factors such as concrete grade, steel fiber content, a/d ratio, etc. on shear strength through this model.

 Block diagram of the problem of calculating the shear resistance of reinforced concrete beams CST

The shear strength of the above high-strength concrete beams according to the model proposed in the thesis follows equations (2-85) and ( 2-83). The block diagram is shown in Figure 2.34.

Begin

Input data: b, h, V f , f c ',f y, L f/ /D f , As, d a

Select ε x (0< ε x <0.003)

Estimated θ:  29  7000  x

Calculate:  0.37 L f V

0.4

f ' ;

1  1500 

(1  V ) ; 

f ci

0.31 

0.18f'c 24w

d a  16

Calculate: f 1 ' cidissolve  zf szcr; ' ci ci ffcolumn; f x (  cicolumn f fcolumn) /  x

Calculate ε' x =f x /E x

Wrong

Ɛ' x ≈ Ɛ x

When Ɛ' x - Ɛ x <1/1000 stop looping

f D

z szcr

etc.

f D

z szcr

etc.

Correct

V  ( f '  0.37 V

L f

f ' cot  f

column) bd ,

when a/d v <2.5;

V  2.5 d / a ( f '  0.37 V

L f

f ' cot  f

column) bd , when a/d ≥2.5

End

Figure 2.34. Block diagram for calculating shear strength for CST reinforced concrete beams

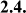
Chapter 2 Conclusion

- Selecting a semi-empirical model to predict the shear strength of CST reinforced concrete beams is very important. There are many semi-empirical models that can predict the shear strength of CST reinforced concrete beams, however, the researcher chose a simple modified Compression Field model to predict the shear strength of CST reinforced concrete beams due to the above analysis.

- In the simple modified compression field model, the tensile work of concrete is considered. For reinforced concrete beams, in addition to the tensile participation of the concrete after cracking, there is also the participation of steel fiber reinforcement.

- As we know, after the concrete cracks, the steel fiber reinforcement begins to participate in tensile strength. The contribution of the steel fiber reinforcement after the concrete cracks depends on the adhesion between the fiber and the concrete. The factors affecting the tensile strength after cracking of the reinforced concrete are fiber content, fiber shape, fiber length and concrete grade. In which, fiber content is the most important factor that greatly affects the tensile strength of the reinforced concrete. Therefore, the construction of the function of tensile strength depending on fiber content and other parameters to evaluate the contribution of steel fiber reinforcement to the tensile strength after cracking was carried out by the researcher. Because it is difficult to directly pull the reinforced concrete sample, the standard cylindrical splitting test was carried out.

- NCS used 2 types of fibers as presented above, with varying fiber content, designed the composition for a high-strength concrete mixture of 70MPa. Adjusted the composition for 7 CST BTCĐC mixes and conducted casting of 105 samples for splitting and 21 samples to test the compressive strength of each calculated mix.

- Based on the results of the split compression test with 105 samples of CST reinforced concrete pillars, using the linear regression method, a formula was developed to calculate the split compression strength of CST reinforced concrete after cracking according to the fiber content (2-82).

- Combining the model with the model for calculating the shear resistance of the selected reinforced concrete beam in section 2.2.3, the researcher has built a formula for calculating the shear resistance of the reinforced concrete beam for the two cases a/d ≥ 2.5 and a/d < 2.5 as in (2-85) and ( 2-83).

- Build a block diagram for the problem of calculating the shear strength of reinforced concrete beams as shown in Figure 2.34.

- Surveying the influence of parameters on the shear strength of CST reinforced concrete beams through the calculation model shows that the shear strength of CST reinforced concrete beams increases rapidly when the fiber content increases. Fiber length also significantly affects the shear strength of CST reinforced concrete beams. The higher the concrete grade, the greater the influence of steel fibers on the shear strength. The inclination angles of the main compressive stress (θ) in the beams calculated according to the proposed model are all less than 45 o .

Chapter 3.

EXPERIMENTAL RESEARCH ON SHEAR BEHAVIOR OF CST CONCRETE REINFORCED BEAMS

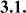
Experimental objectives

Chapter 3 studies the experimental behavior of reinforced concrete beams with design dimensions to verify the model proposed by the researcher in chapter 2. The study of the shear behavior of CST reinforced concrete beams with different CST reinforced concrete mixes is to evaluate the influence of fiber content and fiber type on shear strength. In addition, the experimental study on real beams in chapter 3 also aims to evaluate the behavior in the beam including crack angle, deformation in the compressed concrete, deformation in longitudinal reinforcement and stirrups when subjected to load until failure. The beam size is selected to match the jacking capacity and design standards. The beam must be calculated to arrange the main longitudinal reinforcement and stirrups so that the beam only experiences shear or bending failure within the shear span (a) without being damaged by bending. Casting of CST reinforced concrete beams according to the design dimensions is carried out to verify the shear strength calculation formula proposed above. The 4-point bending beam model was used to test the reference beam according to ASTM C78 [39]. The concentrated force positions were placed at a distance a≥2d from the center of the support. Where d is the distance from the center of the tensile reinforcement to the upper edge of the beam. The concrete grade used in the study was 70MPa, which is consistent with the concrete grade of the sample test. DRAMIX steel fibers with double-hook bending at different sizes were used in the study. Two types of fibers were used: Dramix 3D 80/60 BG with a strength of 1225MPa and Dramix 3D 65/35 BG with a strength of 1345MPa according to DIN 17140D9 and EN 10016-2-C9D standards with low carbon content. The experimental results include data on the shear strength of the beam, the load-deflection curve, the deformation of the concrete in the compression zone, the deformation in the longitudinal reinforcement and the deformation in the stirrups. Experimental data were compared with theory including: shear strength, failure model, and inclination angle of main compressive stress.

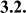
Experimental beam design

3.2.1. Selection of experimental reinforced concrete beam structure

Beam height: According to the provisions in clause 8.3.4.1 in TCVN11823- 2017 standard [4], which stipulates a simple design method for non-prestressed beams or beams with a height of less than 400mm, the values of θ=45 o and β=2 can be taken. Therefore, this is a special case and not a general case. In the thesis, two types of beams are selected.

with height h=450mm and h=400mm to conduct the survey with the purpose of testing beams of the same size. Beam width is chosen b=150mm, based on reference to some experimental models that the authors have researched and selected.

The distance from the concentrated force to the support is a=750mm for beam H=400mm as shown in Figure 3.2 and a=780cm for beam H=450mm. The effective height d=hd o , where do o is the distance from the center of gravity of the longitudinal reinforcement to the bottom edge of the beam cross-section.

The BTCST mixture is calculated as in Appendix 1. When casting each beam, take a sufficient amount of concrete mixture to cast a cylindrical sample to check the concrete grade of that beam.

Sample 2

The number of main reinforcements and the strength of the main reinforcements are selected so that when tested, they are only damaged by shear and not damaged by bending. The longitudinal reinforcement is selected from steel with a diameter of 22mm, with a quantity of 4 bars. The longitudinal reinforcement in the beam uses steel from Hoa Phat Company, with a steel grade of 520 MPa according to TCVN 1651-2008 or ASTM A6115/A615M-08a (USA). The steel samples were taken for testing at the Testing Center of the University of Transport. The results of the steel tensile test are shown in Figure 3.1. The average yield strength of the test samples is f y =512MPa.

Sample 1

Tensile stress, MPa

Tensile strain, %

Sample 3

Tensile strain, %

Figure 3.1. Stress-strain relationship diagram during main longitudinal tensile test

Comment